Circle Game Circle Game

Positive Solution Partcolor {red} {Positive Solution Part} Positive Solution Part

Sort all circles according to their radius, and find a circle JJJ containing I I I in (i,N](i, N](i,N). JJ connects to iii as the father of iii.
A forest can be constructed, and a circle of infinite radius N+1N+1N+1 is a tree.

For tree dpdpdp, let F[i]F[i]F[i] F [i] denote the first iii circle, which does not select the maximum value that can be obtained.
F[i]=max(F[j],w[j])F[i]=sum max(F[j],w[j])F[i]=max(F[j],w[j]), state transition complexity O(N)O(N), tree building complexity O(N2)O(N^2)O(N2).

Consider how to optimize the process of finding a father by dividing all circles into upper and lower arcs.
The upper arc xxx coordinate takes the left endpoint, the lower arc xxx coordinate takes the right endpoint, and arranges according to the xxx coordinate.
Add std:: set < Hu > in order to increase the ranking of the intersections of lines and arcs parallel to the yyy y axis through the current xxx coordinates.
Then you can look for the father in the setsetset set dichotomy, time complexity O (N log N) O (N log N) O (NlogN).

Implementation Partcolor {red} {Implementation Part} Implementation Part

For ease of understanding, give an example__downarrow_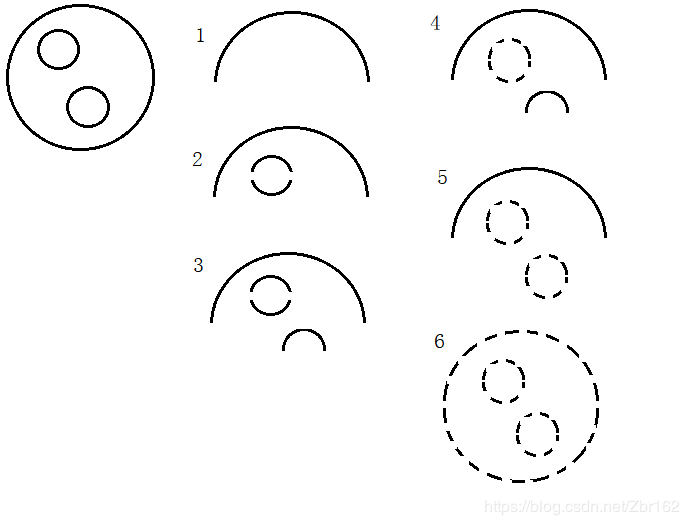

#include<bits/stdc++.h>
#define reg register

int read(){
        char c;
        int s = 0, flag = 1;
        while((c=getchar()) && !isdigit(c))
                if(c == '-'){ flag = -1, c = getchar(); break ; }
        while(isdigit(c)) s = s*10 + c-'0', c = getchar();
        return s * flag;
}

const int maxn = 200005;

int N;
int L_x;
int F[maxn];
int Fa[maxn];

struct circle{ 
        int x, y, r, w;
        double jdzb(int dir){ return y + dir*sqrt(1.0*r*r - (1.0*L_x-x)*(L_x-x)); }
} A[maxn];

struct Hu{ 
        int dir, id;
        bool operator < (const Hu &b) const{ return id==b.id ? dir<b.dir : (A[id].jdzb(dir) < A[b.id].jdzb(b.dir)); }
} B[maxn];

bool cmp(Hu a, Hu b){ return A[a.id].x - a.dir*A[a.id].r < A[b.id].x - b.dir*A[b.id].r; }

std::set <Hu> st;
std::set <Hu>::iterator it;

int main(){
        N = read();
        int Tmp_1 = 0;
        for(reg int i = 1; i <= N; i ++){
                A[i].x = read(), A[i].y = read(), A[i].r = read(), A[i].w = read();
                B[++ Tmp_1] = (Hu){1, i}, B[++ Tmp_1] = (Hu){-1, i};
        }
        std::sort(B+1, B+Tmp_1+1, cmp);
        for(reg int i = 1; i <= Tmp_1; i ++){
                int id = B[i].id, dir = B[i].dir;
                L_x = A[id].x - dir*A[id].r;
                if(dir == 1){
                        if(!st.empty()){ 
                                it = st.upper_bound(B[i]); 
                                if(it != st.end()) Fa[id] = (it->dir==1)?it->id:Fa[it->id];
                        }
                        st.insert((Hu){1, id}), st.insert((Hu){-1, id});
                }else{
                        st.erase((Hu){1, id}), st.erase((Hu){-1, id});
                        F[Fa[id]] += std::max(F[id], A[id].w);
                }
        }
        printf("%d\n", F[0]);
        return 0;
}