Introduction of sorting

When processing data, it is often necessary to search. In order to search quickly and accurately, the data to be processed is usually required to be arranged in order according to the size of key words, so as to adopt efficient search methods.

Basic concept of sorting

1. ranking
Sorting is a kind of operation often carried out in the computer. Its purpose is to adjust a group of "unordered" record sequences to "ordered" record sequences. Generally speaking, the process of arranging disordered data elements by certain methods in order of keywords is called sorting.
2. Internal sorting and external sorting
Sorting can be divided into two categories according to the different memory occupied by data during sorting.
Internal sorting: the whole sorting process is completely in memory;
External sorting: because the amount of record data to be sorted is too large, the memory cannot hold all the data, so sorting can be completed with the help of external memory devices.
3. Stability of sequencing
Stability: suppose that there are two or more records with the same keyword in the file to be sorted
After sorting by some sort method, if the relative order of the elements with the same key remains the same, the sort method
It's stable. On the contrary, if the relative order of these elements with the same keyword changes, the sorting method used is unstable.
Example: a group of student records have been sorted by student number, and now they need to be sorted by final grade. When the grades are the same, the small student number is required to be in the front. Obviously, in this case, a stable sorting method must be selected.
Note: bubbling, inserting, cardinality, merging belong to stable sorting, selection, fast, hill, belong to unstable sorting.

Sorting classification and complexity analysis

Complexity and stability of time and space
Explanation of time and space complexity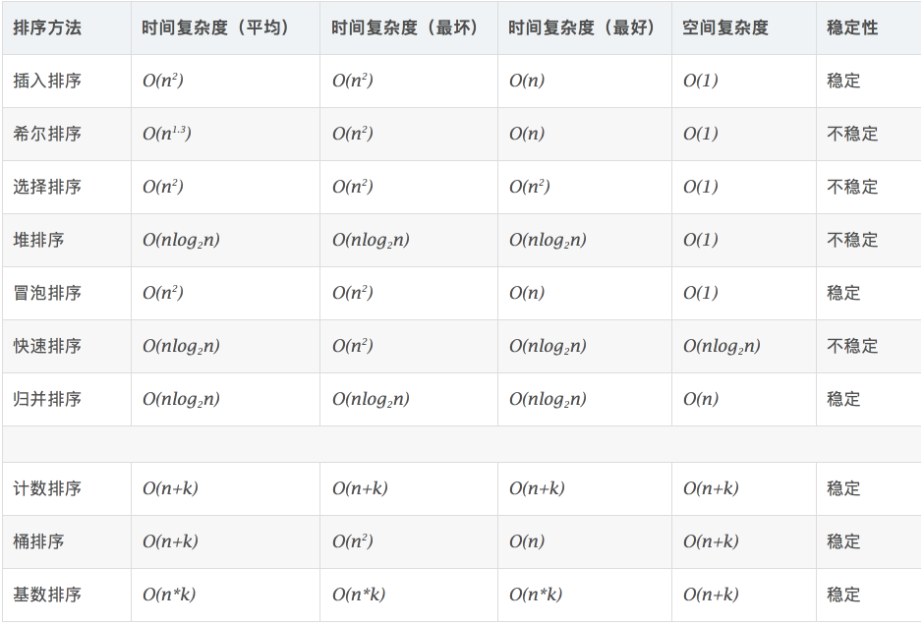

Details of common sorting

Insertion sort

1. Direct insertion sorting
Basic ideas:
In a set of numbers to be sorted, suppose that the first n-1 numbers have been ordered, now insert the nth number into the previous ordered number series, so that the nth numbers are also ordered. Repeat the cycle until all are in order.
Advantages: stable, fast.
Disadvantages: the number of comparisons is not certain. The more comparisons are, the more data moves after the insertion point. Especially when the total amount of data is huge, but the linked list can solve this problem, although there will be additional memory overhead.
Process: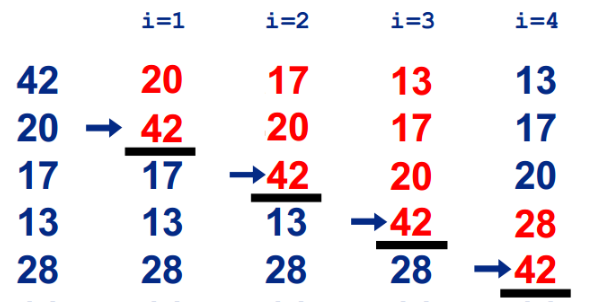

Code implementation:

// Direct insert sort
void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int next = a[end + 1];//Save the value of the next number to avoid being overwritten by the next time
		while (end >= 0 && a[end]>next)//Compare the parts arranged in the front from the back to the front. If there is a large part, it will be covered later. If there is a large part, it will be covered later. If there is no larger part, it will be covered later. If there is no larger part, it will be covered until it is no larger than the next to judge the insertion, it will jump out of the loop,
		{
			a[end+1] = a[end];
			end--;
		}
		a[end + 1] = next; //And then assign the next to be inserted at the termination position
	}
}

Summary of characteristics of direct insertion sorting:

1. The closer the element set is to order, the more efficient the direct insertion sorting algorithm is
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable
5. Applicability: insertion sorting is not suitable for sorting applications with large amount of data. However, if the amount of data to be sorted is small, insert sorting is a good choice.

2. Hill sorting
Basic ideas:
In a group of numbers to be sorted, they are divided into several subsequences according to a certain increment, and the subsequences are inserted and sorted respectively.
Then gradually reduce the increment and repeat the above process. Until the increment is 1, at this time, the data sequence is basically in order, and finally the insertion sorting is performed.
Process: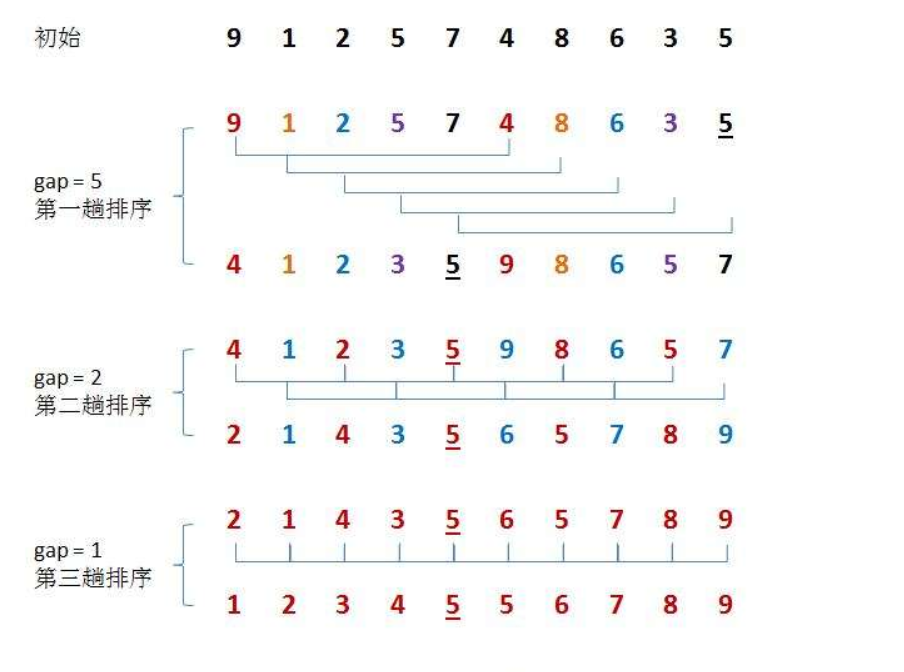

code implementation

// Shell Sort
void ShellSort(int* a, int n)
{
	int gap = n;
	//It cannot be written as greater than 0 because the value of gap is always > = 1,
	while (gap > 1)
	{
		gap = gap / 3 + 1;   //Set increment / / gap should be changed to 1 at last, which is the end of sorting, so add 1 here
		for (int i = 0; i < n - gap; i++)
		{
			    // In this case, you can just change the 1 of insertion sort to gap
				//But it's not like sorting out a group and going back
				//Sort the other group, but only go through the whole group once
				//In this way, only one part of each group of data is arranged at a time
				//After the end of the cycle, the data sorting of all groups is completed
			int end = i;
			int next = a[end + gap];
			while (end>=0 && a[end] > next)
			{
				a[end + gap] = a[end];
				end -= gap;
			}
			a[end + gap] = next;
		}
	}
}

Summary of the characteristics of hill sorting:

1. Hill sort is an optimization of direct insertion sort.
2. When gap > 1, they are all pre ordered, in order to make the array closer to order. When gap == 1, the array is almost ordered, so it will be very fast. In this way, the overall effect of optimization can be achieved.
3. The time complexity of hill sorting is not easy to calculate, so it needs to be deduced. The average time complexity is O(N1.3-N2)
4. Stability: unstable

Selection sort

1. Simple selection and sorting
Basic ideas:
Each time, select the smallest (or largest) element from the data elements to be sorted, and store it at the beginning of the sequence until all the data elements to be sorted are finished.
Process: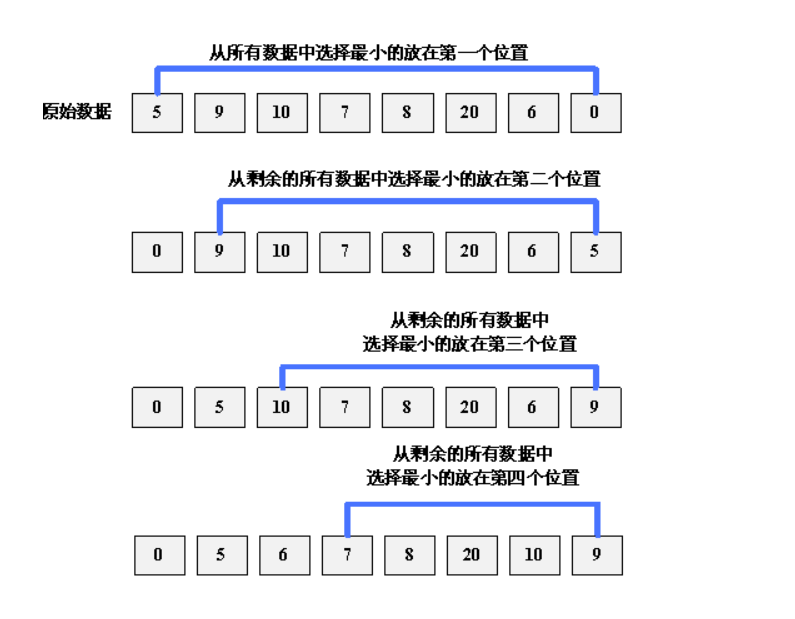

Code implementation:

 Selection sort
void SelectSort(int* a, int n)
{
	for (int i = 0; i < n; i++)             
	{
		int min = i;
		for (int j = i+1; j < n; j++)
		{
			if (a[j] < a[min])//Until the leftmost find the lowest subscript
			{
				min = j;
			}
		}
		swap(&a[i], &a[min]);//The small ones will be switched to the front, and then the next round of comparison and selection
	}

}

Summary of characteristics of direct selection sorting:

1. It's easy to understand how to think by direct selection and sorting, but the efficiency is not very good. Rarely used in practice
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: unstable

2. heap sort
Basic ideas:
Heap sort is a sort algorithm designed by using the data structure of heap tree. It is a kind of selective sort. It selects data through the heap. It should be noted that a large pile should be built in ascending order and a small pile should be built in descending order.
Process:
Rank in ascending order, build a large number, and then choose judgment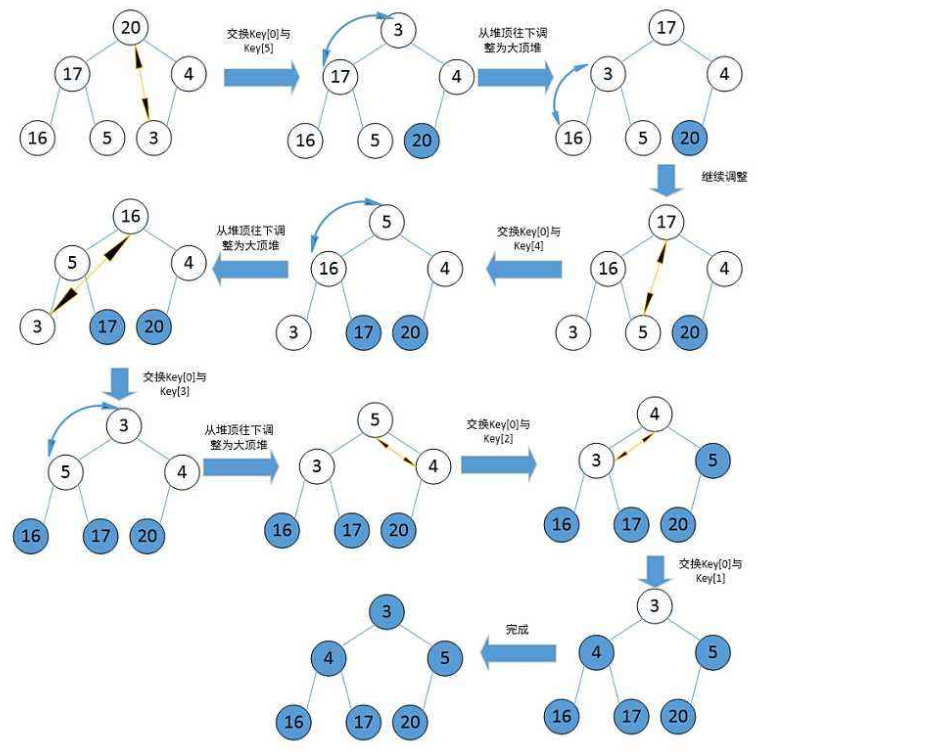

code implementation

// Heap sort
void AdjustDwon(int* a, int n, int root)//Downward adjustment algorithm pile
{
	int parent = root;
	int child = parent * 2 + 1;
	while (child < n)
	{
		if ((child + 1) < n && a[child] < a[child + 1])
		{
			child++;
		}
		if (a[child]>a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	// To build a heap, start from the root (index is (n - 2) / 2) on the last two leaves
	// Build the smallest heap first until a[0] (the largest heap)
	// This is equivalent to adding a new one to the existing heap
	// Root element, then adjust down to make the entire binary tree
	// Re satisfy the properties of the heap
	for (int i = (n - 2) / 2; i >= 0; i--)//Build a lot
	{
		AdjustDwon(a, n, i);
	}
	int end = n - 1;//The last number is exchanged with the large number at the top of the heap. The second largest number is adjusted to the top of the heap. It is exchanged. It is adjusted
	while (end > 0)
	{
		swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);
		end--;
	}
}

Summary of characteristics of heap selection sorting:

1. Heap sorting uses heap to select data, which is much more efficient.
2. Time complexity: O(N*logN)
3. Space complexity: O(1)
4. Stability: unstable

Exchange sort

1. Bubble sorting
Basic idea: the two numbers are relatively large, the larger number sinks, and the smaller number rises
Process: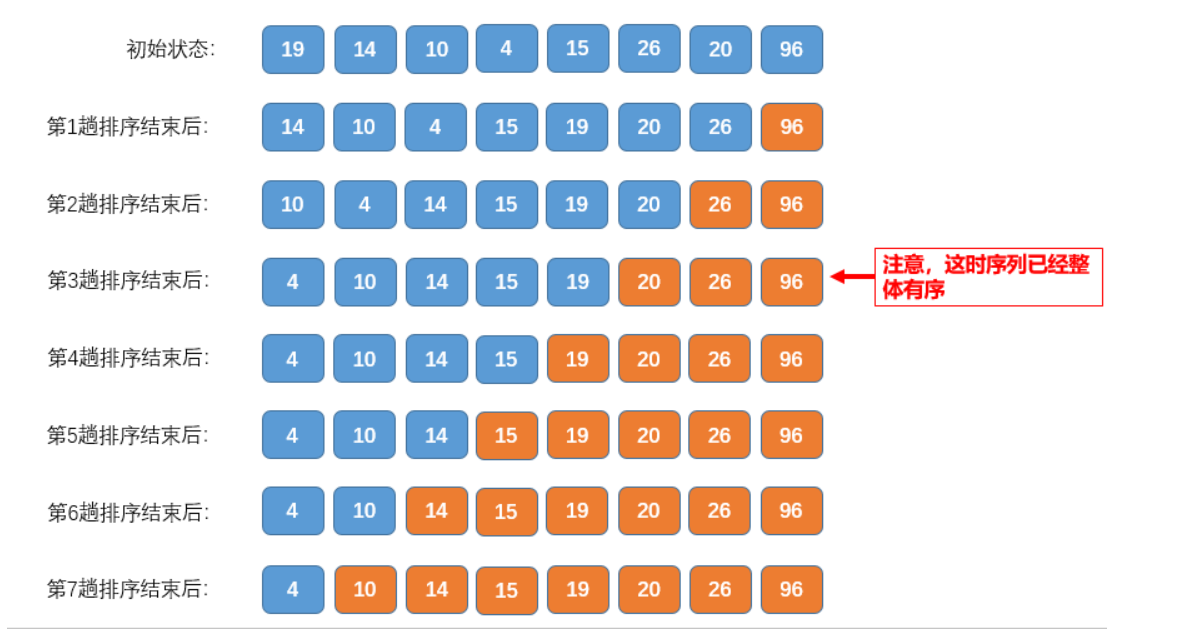

Implementation code:

// Bubble sort
void BubbleSort(int* a, int n)
{
	int end = n - 1;
	while (end > 0)// Control trips
	{
		int flag = 0;//It is possible that the array to be sorted has reached an ordered level this time, and there is no need to run the next number of times, so set a target value to record this situation
		for (int i = 1; i <= end; i++)//One by one, until the end of this trip
		{
			if (a[i - 1] > a[i])
			{
				swap(&a[i - 1], &a[i]);
				flag = 1;
			}
		}
		if (flag == 0)//It's already in order, so you don't have to lie down next and jump out
		{
			break;
		}
		end--;
	}
}

Summary of bubble sorting characteristics:

1. Bubble sorting is a very easy to understand sort
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable

2. Quick sorting
Fast sorting is a kind of exchange sorting method of binary tree structure proposed by Hoare in 1962.
Basic idea: (divide and rule)
1. First, take a number from the sequence as the key value;
2. Put all numbers smaller than this number on its left side, and all numbers greater than or equal to it on its right side;
3. Repeat the second step for the left and right small sequences until there is only one number in each interval.
Process:
The common ways to divide the interval into left and right halves according to the reference value are as follows:

1. Middle of three
2. Digging method
3. Before and after pointer version
   Detailed explanation of three versions of fast typesetting
   The first specific process (the most common Division: select the first or last element as the reference value):

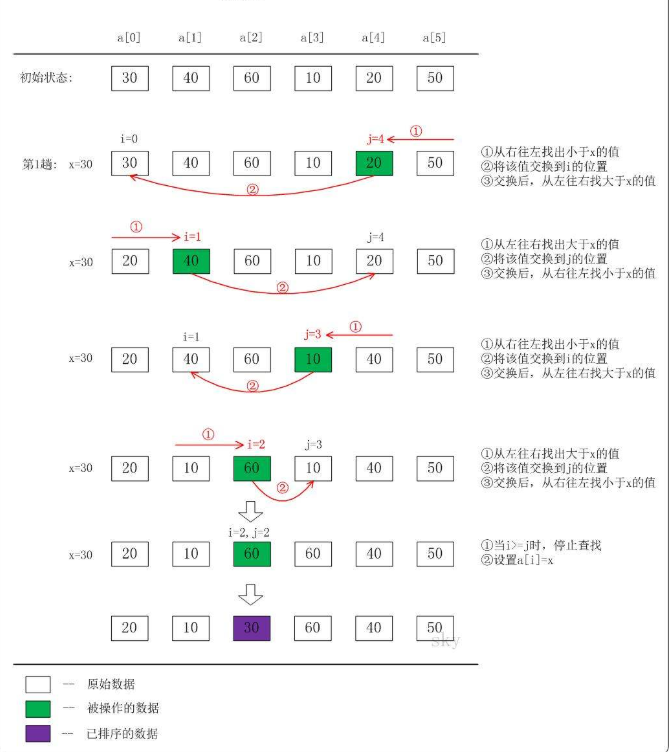
Code implementation:
Common version implementation:

//Note to normal version: select the leftmost as the reference value, and compare from the rightmost
int PartSort(int *a, int left, int right)
{
	int key = a[left];
	int start = left;
	while (left < right)
	{
		while (left < right && a[right]>=key)
		{
			right--;
		}
		while (left < right && a[left] <= key)
		{
			left++;
		}
		swap(&a[left], &a[right]);
	}
	swap(&a[left], &a[start]);
	return  left;
}
void QuickSort(int* a, int left, int right)
{
	//If (left > = right) / / in special case 1, 3, 5, 4, when the first row is in the first row, 1 is the benchmark, and the end does not find the smaller one, which will be subtracted until it is in itself. At this time, left=right, and the keyindex is returned as the left that is not moving; when the next row is recursive, left is 0, which is greater than - 1 of the keyindex-1, there is no meaningful recursive number on the left. It means that if there is no region or only one data, there is no recursion sort
	//	return;
	if (left < right)
	{
		if (left-right +1 < 10)//Inter cell Optimization: if the amount of data in the interval is less than a certain value, there is no need to use fast row recursion. Data with small amount of sorting can still be sorted by inserting
		{
			InsertSort(a+left, right-left + 1); //It's also the transmission interval
		}
		else
		{
			int keyindex = PartSort3(a, left, right);
			// [left, keyindex-1] keyindex [keyindex + 1, right] binary tree structure left interval reference value right interval continue recursion
			QuickSort(a, left, keyindex - 1);//The left side of the reference value (greater than it) continues to be divided
			QuickSort(a, keyindex + 1, right);//The right side of the reference value (less than it) also continues
			//Until the smallest is in order
		}
	}
}

Summary of quick sorting features:

1. The overall comprehensive performance and usage scenarios of quick sorting are relatively good
2. Time complexity: O(N*logN)
3. Spatial complexity: O(logN)
4. Stability: unstable
   Disadvantages: in the worst case, the initial record is ordered. At this time, the time complexity is O(N^2). In fact, fast sorting is more effective in the case of "disordered" initial record.

Merge sort

Basic ideas:
The array is divided into two groups A and B. if the data in these two groups are in order, then it is very convenient to sort these two groups of data.
Group A and B can be divided into two groups. By analogy, when the divided group has only one data, it can be considered that the group has reached order, and then merge the two adjacent groups. In this way, the merging and sorting are completed by decomposing the sequence recursively and then merging the sequence.
Process: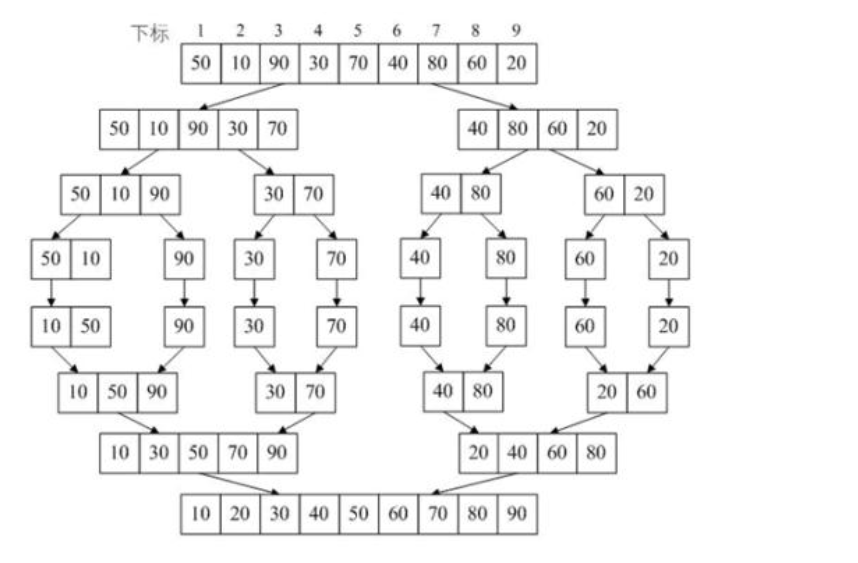

Recursive implementation code:

//Merge sort is first divided in merge
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)  //Until there is only one element left in each group, stop dividing and prepare to merge
	{
		return;
	}
	int mid = left + ((right - left) >> 1);
	_MergeSort(a, left, mid, tmp);     //Recursively partition first, then stack and merge
	_MergeSort(a, mid + 1, right, tmp);
	// [left, mid]
	// [mid+1, right]
	int i = left, j = mid;
	int x = mid + 1, z = right;
	int k = left;
	
	//There will be two ordered sequences a[left...mid] and a[mid...right] combined.
	while (i <= j && x<=z)
	{
		if (a[i] <=a[x])
		{
			tmp[k++] = a[i++];
		}
		else
		{
			tmp[k++] = a[x++];
		}
	}
	while(i <= j)
		tmp[k++] = a[i++];
	while(x <= z)
		tmp[k++] = a[x++];
	for (i = 0; i<k; i++)
		a[left + i] = tmp[i];
	//memcpy(a + left, tmp + left, sizeof(int)*(right - left+1 ));
}
// Recursive implementation of merge sort
void MergeSort(int* a, int n)
{
	int* tmp = (int *)malloc(sizeof(int)*n);
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);

}

Summary of characteristics of merging and sorting:
The efficiency of merging and sorting is relatively high. It takes logN steps to set the length of the sequence as N, and divide the sequence into small sequence. Each step is a process of merging the sequence. The time complexity can be recorded as O(N), so the total is O(NlogN). Because merge sorting operates in adjacent data every time, several sorting methods (fast sorting, merge sorting, heap sorting) of merge sorting in O(NlogN) are also efficient.

1. The disadvantage of merging is that it needs O(N) space complexity. The thinking of merging and sorting is more to solve the problem of sorting out of disk.
2. Time complexity: O(N*logN)
3. Space complexity: O(N)
4. Stability: stable

Summary

Through the comprehensive analysis and comparison of various sorting methods, the following conclusions can be drawn:
1. The simple sorting method is generally only used in the case of small n (for example, n < 30). When the records in the sequence are "basically ordered", the best sorting method is to insert people directly. If there is a large amount of data in the records, the simple selection sorting method with a small number of moves should be adopted.
2. The average time complexity of fast sorting, heap sorting and merge sorting is 0(nlogn), but the experimental results show that fast sorting is the best of all sorting methods in terms of average time performance. Unfortunately, the worst-case time for a quick sort
The performance is 0(n^2). The worst-case time complexity of heap sort and merge sort is still 0 (nlogn). When n is large, the time performance of merge sort is better than heap sort, but it needs the most auxiliary space.
3. The simple sorting method can be combined with the better sorting method. For example, in the fast sorting, when the length of the delimited molecular interval is less than a certain value, the direct interpolation sorting method can be used instead; or the sequence to be sorted can be divided into several subsequences, and the direct interpolation sorting can be carried out respectively, and then the merge sorting method can be used to merge the ordered subsequences into a complete ordered sequence.
4. The time complexity of Radix sorting can be written as 0(dn). Therefore, it is most suitable for a sequence with a large n value and a small d number of keywords. When D is much less than N, its time complexity is close to 0(n).
5. From the point of view of the stability of sorting, among all the simple sorting methods (insertion, simple selection, bubbling), the simple selection sorting is unstable, and all other simple sorting methods are stable. However, among those sorting methods with better time performance, Hill sort, fast sort and heap sort are all unstable, only the merge sort cardinal sort is stable.

To sum up, each sorting method has its own characteristics, and no method is absolutely optimal. The proper sorting method should be selected according to the specific situation, and multiple methods can also be used together.