Bubble sorting
Sorting principle:
- Compare adjacent elements. If the former element is larger than the latter, exchange the positions of the two elements.
- Do the same for each pair of adjacent elements, from the first pair of elements to the last pair of elements at the end. The final position is the maximum.
Bubble sorting API design
| Class name | Bubble | describe |
| Construction method | Bubble() | Create a Bubble object |
| Member method | public static void sort(Comparable[] a) | Sort the elements in the array |
| private static boolean greater(Comparable v, Comparable w) | Judge whether v is greater than w | |
| private static void exch(Comarable[] a, int i, int j) | Swap the values at index i and index j in the array |
Code implementation of bubble sorting:
public class Bubble {
/**
* Sorting method
*/
public static void sort(Comparable[] a){
for (int i = a.length-1; i > 0; i--){
for (int j = 0; j < i; j++){
if (greater(a[j],a[j+1])){
exch(a,j,j+1);
}
}
System.out.println("The first"+(a.length - i)+"Secondary sorting result"+Arrays.toString(a));
}
}
/**
* Compare element sizes
*/
private static boolean greater(Comparable v, Comparable w){
return v.compareTo(w) > 0;
}
/**
* Swap element location
*/
private static void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
}
The test code is as follows
public class Test {
public static void main(String[] args) {
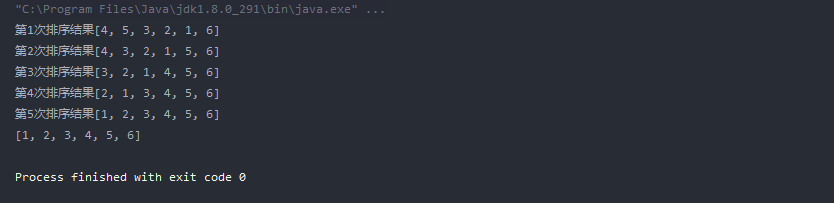
Integer[] a = {4,5,6,3,2,1};
Bubble.sort(a);
System.out.println(Arrays.toString(a));
}
}
Test result printing
Time complexity analysis of bubble sorting
Bubble sorting uses a double-layer for loop, in which the loop body of the inner loop is the real sorting code. Therefore, we analyze the time complexity of bubble sorting, mainly the execution times of the inner loop body.
In the worst case, that is, the sorting elements are in reverse order of {6,5,4,3,2,1}, then:
The number of element comparisons is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2 = N^2/2-N/2
The number of element exchanges is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2 = N^2/2-N/2
The total number of executions is:
N^2/2-N/2 + N^2/2-N/2 = N^2-N
Therefore, the time complexity of bubble sorting is O(N^2)
Select sort
Select sorting principle:
- During each traversal, it is assumed that the element exported from the first index is the minimum value, and it is compared with the values at other indexes in turn. If the value at the current index is greater than the value at some other index, it is assumed that the value at some other index is the minimum value, and finally the index where the minimum value is located can be found.
- Swap the values at the first index and at the index where the minimum value is located.
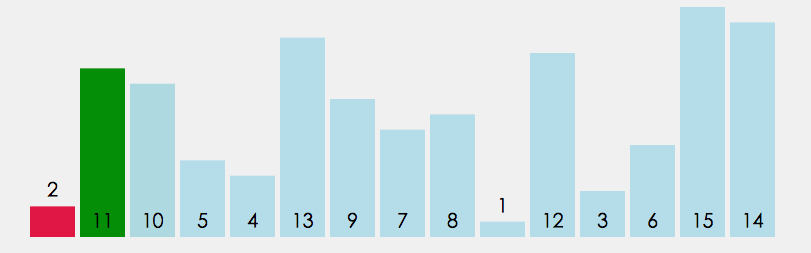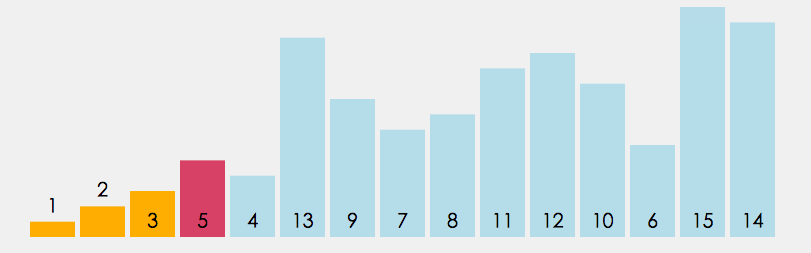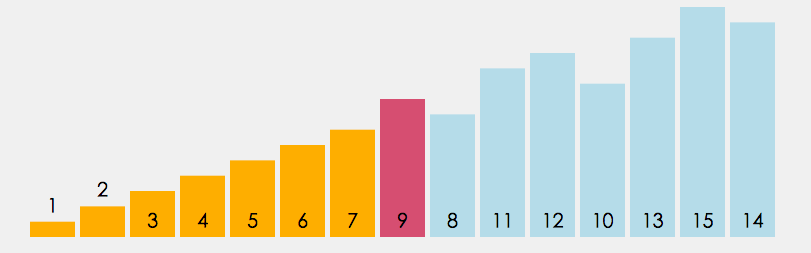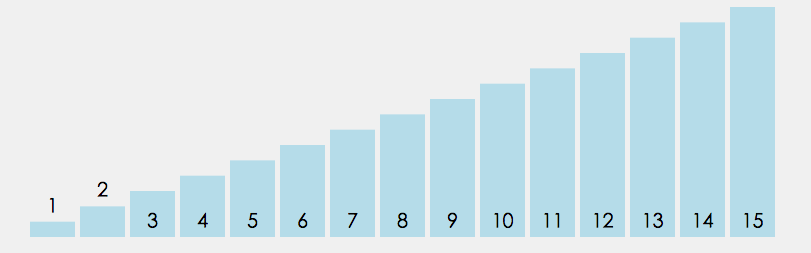
Select Sorting API design
| Class name | Selection | describe |
| Construction method | Selection() | Create a Selection object |
| Member method | public static void sort(Comparable[] a) | Sort the elements in the array |
| private static boolean greater(Comparable v, Comparable w) | Judge whether v is greater than w | |
| private static void exch(Comarable[] a, int i, int j) | Swap the values at index i and index j in the array |
Select the code implementation of sorting
public class Selection {
/**
* Sorting method
*/
public static void sort(Comparable[] a){
for (int i = 0; i < a.length - 1; i++){
//Set the minimum index value to i
int minIndex = i;
for (int j = i+1; j < a.length; j++){
if (greater(a[minIndex],a[j])){
//Exchange minimum index
minIndex = j;
}
}
//Swap values at i index and minIndex index
exch(a,i,minIndex);
System.out.println("The first"+(i+1)+"Secondary sorting result"+ Arrays.toString(a));
}
}
/**
* Compare element sizes
*/
private static boolean greater(Comparable v, Comparable w){
return v.compareTo(w) > 0;
}
/**
* Swap element location
*/
private static void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
}Test code
public class Test {
public static void main(String[] args) {
Integer[] a = {4,5,6,3,2,1,9};
Selection.sort(a);
System.out.println(Arrays.toString(a));
}
}The printing results are as follows:

Select sorting time complexity analysis:
The double-layer for loop is used for selective sorting, in which the outer loop completes data exchange and the inner loop completes data comparison. Therefore, we analyze the time complexity of selective sorting, mainly analyzing the number of exchanges and data comparison.
The number of element comparisons is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2 = N^2/2-N/2
The number of element exchanges is:
N-1
The total number of executions is:
N^2/2-N/2 + N-1 = N^2+N/2 -1
Therefore, the time complexity of sorting is O(N^2).
Insert sort
Insert sort principle:
- Divide all elements into two groups, sorted and unordered.
- Find the first element in the unordered group and insert it into the sorted group.
- Flashback traverses the sorted elements and compares them with the elements to be inserted in turn until an element less than or equal to the element to be inserted is found. After that, put the element to be inserted in this position for a long time, and move other elements one bit backward.
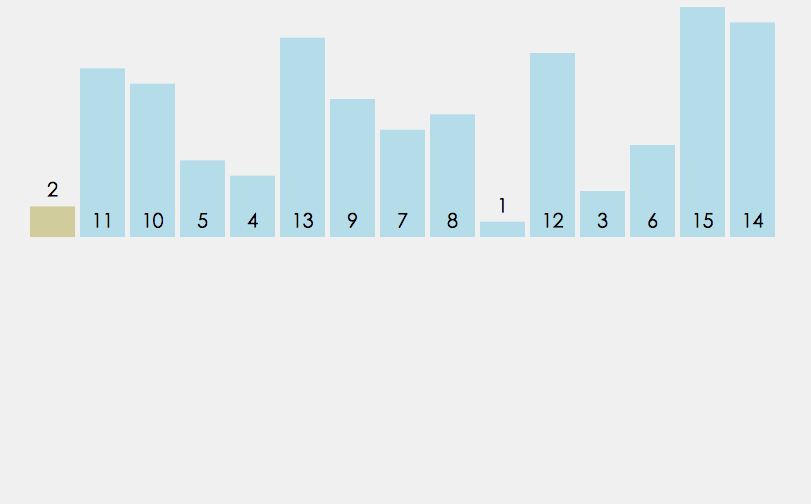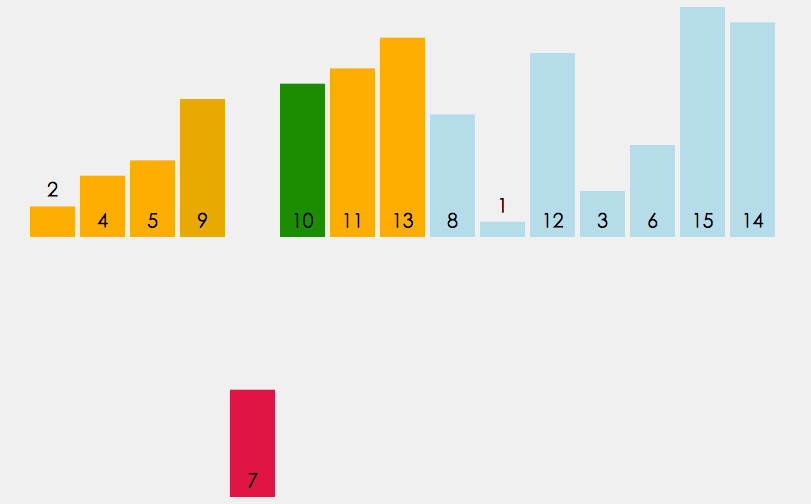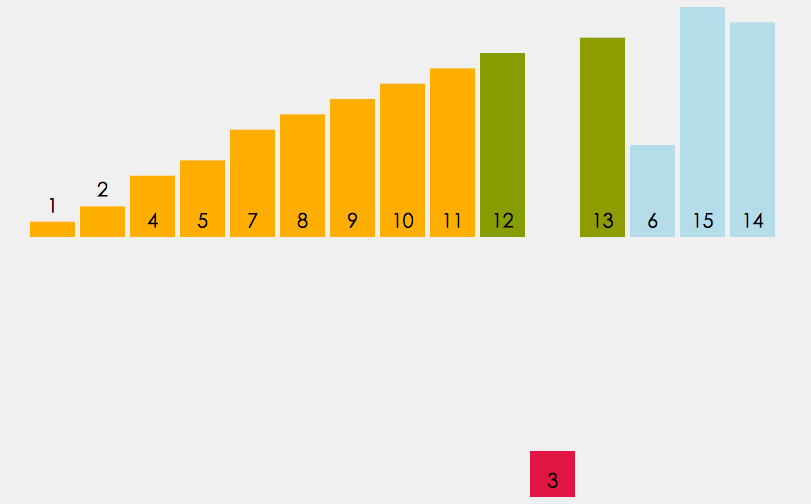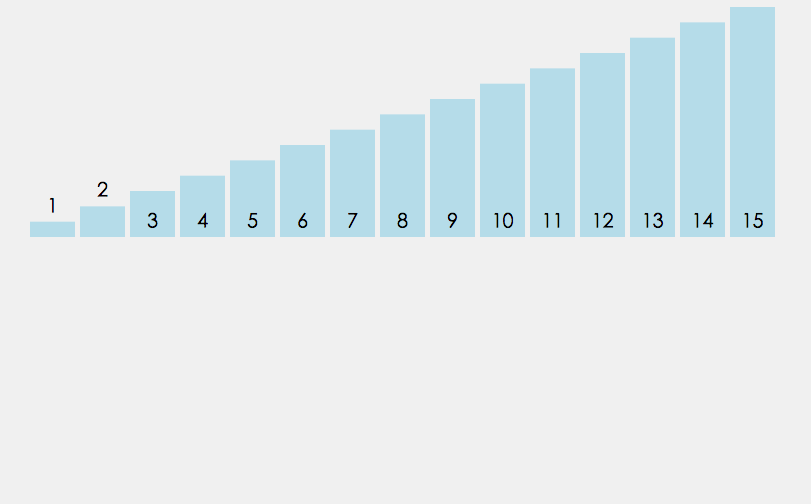
Insert sort API design
| Class name | Insertion | describe |
| Construction method | Insertion() | Creating an Insertion object |
| Member method | public static void sort(Comparable[] a) | Sort the elements in the array |
| private static boolean greater(Comparable v, Comparable w) | Judge whether v is greater than w | |
| private static void exch(Comarable[] a, int i, int j) | Swap the values at index i and index j in the array |
Insert sort code implementation
public class Insertion {
/**
* Sorting method
*/
public static void sort(Comparable[] a){
for (int i = 1; i < a.length; i++){
for (int j = i; j > 0; j--){
if (greater(a[j-1],a[j])){
exch(a,j-1,j);
}else{
break;
}
}
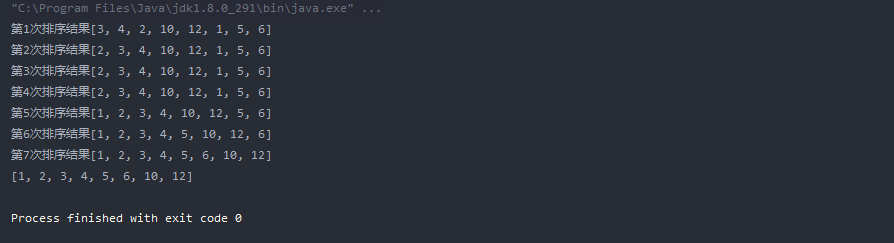
System.out.println("The first"+(i)+"Secondary sorting result"+ Arrays.toString(a));
}
}
/**
* Compare element sizes
*/
private static boolean greater(Comparable v, Comparable w){
return v.compareTo(w) > 0;
}
/**
* Swap element location
*/
private static void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
}Test code
public class Test {
public static void main(String[] args) {
Integer[] a = {4,3,2,10,12,1,5,6};
Insertion.sort(a);
System.out.println(Arrays.toString(a));
}
}Test result printing
Insertion sort time complexity analysis
Insert sorting uses a double-layer for loop, in which the loop body of the inner loop is the code that really completes sorting, so the time complexity mainly analyzes the execution times of the inner loop body.
The number of element comparisons is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2 = N^2/2-N/2
The number of element exchanges is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2 = N^2/2-N/2
The total number of executions is:
N^2/2-N/2 + N^2/2-N/2 = N^2-N
Therefore, the insertion sort time complexity is O(N^2).
Shell Sort
Hill sorting principle:
- Select a growth amount h and group the data according to the growth amount h as the basis for data grouping.
- Insert and sort each group of data divided into groups.
- Reduce the growth to 1 and repeat the second step.

Determination of growth amount H: there is no fixed rule for the value of growth amount h. here we adopt the following rule:
int N = a.length;
//Determine the maximum value of growth h
int h=1;
while(h<N/2){
h=h*2+1;
}
//The reduction rule of h is
h=h/2;API design for Hill sorting:
| Class name | Shell | describe |
| Construction method | Shell() | Create Shell object |
| Member method | public static void sort(Comparable[] a) | Sort the elements in the array |
| private static boolean greater(Comparable v, Comparable w) | Judge whether v is greater than w | |
| private static void exch(Comarable[] a, int i, int j) | Swap the values at index i and index j in the array |
Hill sort code implementation
public class Shell {
/**
* Sorting method
*/
public static void sort(Comparable[] a){
int len = a.length;
int h = 1;
while (h < len/2){
h = h*2+1;
}
while (h>=1){
//Find the element to insert
for (int i=h;i<len;i++){
//Insert a[i] into a[i-h],a[i-2h] In the sequence
for (int j=i;j>=h;j-=h){
//Compare a[j] with a[j-H] and a[j-2h] successively,
// If a[j] is small, the exchange position. If it is not less than, a[j] is large, the insertion is completed
if (greater(a[j-h],a[j])){
exch(a,j,j-h);
}else{
break;
}
}
}
System.out.println("h="+h+",Sorting results:"+ Arrays.toString(a));
h/=2;
}
}
/**
* Compare element sizes
*/
private static boolean greater(Comparable v, Comparable w){
return v.compareTo(w) > 0;
}
/**
* Swap element location
*/
private static void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
}
Test code:
public class Test {
public static void main(String[] args) {
Integer[] a = {4,3,2,10,12,1,5,6};
Shell.sort(a);
System.out.println(Arrays.toString(a));
}
}Test print results:
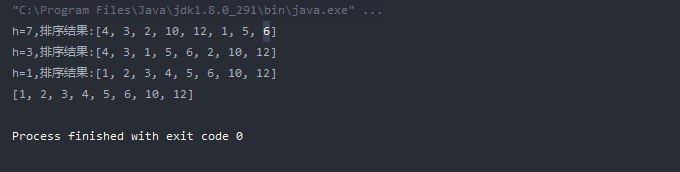
Merge sort
Principle of merging and sorting:
- Split a set of data into two subgroups with equal elements as far as possible, and continue to split each subgroup until the number of elements in each subgroup after splitting is 1.
- Merge two adjacent subgroups into an ordered large group.
- Repeat step 2 until there is only one group.
Merge sort API design
| Class name | Merge | describe |
| Construction method | Merge() | Create a Merge object |
| Member method | public static void sort(Comparable[] a) | Sort the elements in the array |
| private static void sort(Comparable[] a, int lo, int hi) | Sorts the elements of the array from index lo to index hi | |
| private static void merge(Comparable[] a, int lo, int mid, int hi) | From index lo to index mid is a subgroup, and from index mid+1 to index hi is another subgroup. Merge the data of the two subgroups in array a into an ordered large group (from index lo to index HI) | |
| private static boolean less(Comparable v, Comparable w) | Judge whether v is less than w | |
| private static void exch(Comarable[] a, int i, int j) | Swap the values at index i and index j in the array | |
| Member variable | private static Comparable[] assist | Auxiliary array required to complete the merge operation |
The merge sorting algorithm code is as follows:
public class Merge {
private static Comparable[] assist;
/**
* Sorting method
*/
public static void sort(Comparable[] a){
assist = new Comparable[a.length];
int lo = 0;
int hi = a.length -1;
sort(a, lo, hi);
}
/**
* Sorts the elements from lo to hi in the array
*/
private static void sort(Comparable[] a, int lo, int hi){
if (hi <= lo){
return;
}
int mid = lo + (hi - lo)/2;
//Sort the elements from lo to mid
sort(a, lo, mid);
//Sort the elements between mid+1 and hi
sort(a, mid+1, hi);
//Merge the data from lo to mid and the data from mid to hi
merge(a,lo,mid,hi);
}
/**
* In the array, from lo to mid is a group, and from mid+1 to hi is a group. Merge the two groups of data
*/
private static void merge(Comparable[] a, int lo, int mid, int hi){
//Define a pointer to the index in the assist array that starts filling data
int i = lo;
//Defines a pointer to the first element of the first set of data
int p1 = lo;
//Define a pointer to the first element of the second set of data
int p2 = mid + 1;
//Compare the size of the elements in the left group and the right group. Whichever is smaller, fill which data into the assist array
while (p1 <= mid && p2 <= hi){
if (less(a[p1],a[p2])){
assist[i++] = a[p1++];
}else{
assist[i++] = a[p2++];
}
}
//After the above cycle ends, if the condition for exiting the cycle is P1 < = mid, it proves that the data in the left group has been merged,
// If the condition for exiting the cycle is P2 < = Hi, it proves that the data of the right group has been filled;
//Therefore, you need to continue to fill the unfilled data into the assist. / / only one of the following two loops will be executed
while (p1<=mid){
assist[i++] = a[p1++];
}
while (p2<=hi){
assist[i++] = a[p2++];
}
//So far, the elements from lo to hi in the assist array are ordered, and then copy the data to the corresponding index in the a array
for (int index=lo; index <= hi; index++){
a[index] = assist[index];
}
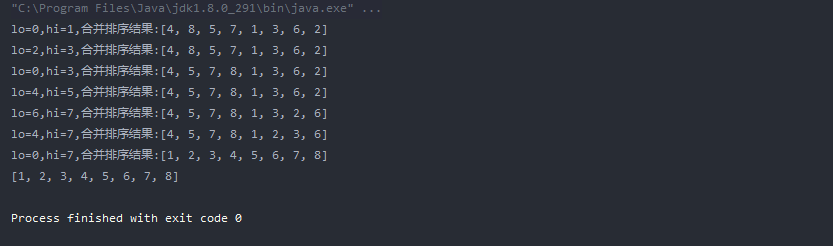
System.out.println("lo="+lo+",hi="+hi+",Merge sort results:"+ Arrays.toString(a));
}
/**
* Compare element sizes
*/
private static boolean less(Comparable v, Comparable w){
return v.compareTo(w) < 0;
}
/**
* Swap element location
*/
private static void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
}
The test code is as follows:
public class Test {
public static void main(String[] args) {
Integer[] a = {8,4,5,7,1,3,6,2};
Merge.sort(a);
System.out.println(Arrays.toString(a));
}
}Test print results:
Quick sort
Quick sort principle:
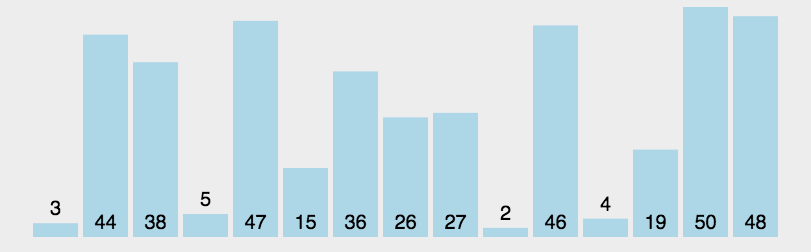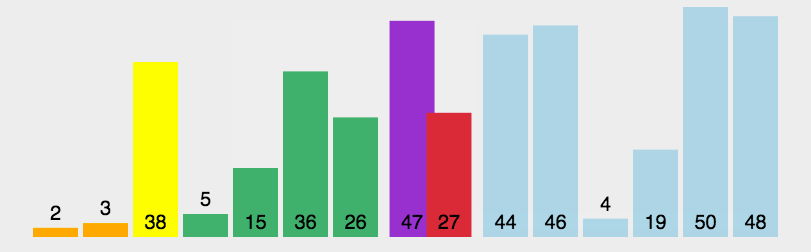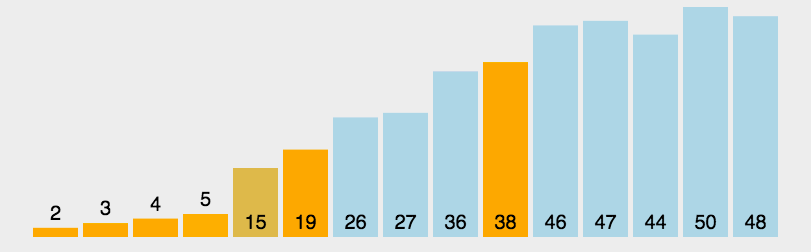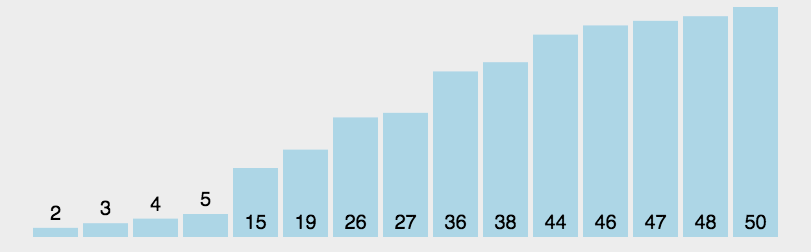
- First, set a boundary value, and divide the array into left and right parts through the boundary value.
- Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value.
- Then, the data on the left and right can be sorted independently. For the array data on the left, you can take a boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.
- By repeating the above process, we can see that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed.
Quick sort API design
| Class name | Quick | describe |
| Construction method | Quick() | Create Quick object |
| Member method | public static void sort(Comparable[] a) | Sort the elements in the array |
| private static void sort(Comparable[] a, int lo, int hi) | Sorts the elements of the array from index lo to index hi | |
| private static int partition(Comparable[] a, int lo, int hi) | Sorts the elements in array a from index lo to index hi | |
| private static boolean less(Comparable v, Comparable w) | Judge whether v is less than w | |
| private static void exch(Comarable[] a, int i, int j) | Swap the values at index i and index j in the array |
Segmentation principle:
The basic idea of dividing an array into two subarrays:
- Find a reference value and point to the head and tail of the array with two pointers respectively;
- First, find the tail to the head and start searching for an element smaller than the reference value. When the element is searched, it will stop, and record the position of the pointer;
- Then start to search for an element larger than the reference value from the head to the tail, stop when the element is searched, and record the position of the pointer;
- Exchange the elements of the current left pointer position and the right pointer position;
- Repeat steps 2, 3 and 4 until the value of the left pointer is greater than that of the right pointer.
Quick sort code implementation:
public class Quick {
/**
* Sorting method
*/
public static void sort(Comparable[] a){
int lo = 0;
int hi = a.length - 1;
sort(a,lo,hi);
}
/**
* Sorts the elements from lo to hi in the array
*/
private static void sort(Comparable[] a, int lo, int hi){
if (hi <= lo){
return;
}
//Slice the elements from lo to hi in the a array
int partition = partition(a, lo, hi);
//Sort the elements in the left group
sort(a,lo,partition-1);
//Sort the elements in the right group
sort(a,partition+1,hi);
}
/**
* Split the array
*/
private static int partition(Comparable[] a, int lo, int hi){
//Take the leftmost value as the reference value
Comparable key = a[lo];
//Defines a left pointer that initially points to the leftmost element position
int left = lo;
//Defines a right pointer that initially points to the next position of the rightmost element
int right = hi + 1;
//Perform segmentation
while (true){
//Scan from right to left to find an element smaller than the reference value
//The loop stops, proving that an element smaller than the reference value is found
while (less(key,a[--right])){
if (right == lo){
break;
}
}
//Then scan from left to right to find an element larger than the reference value
//The loop stops, proving that an element larger than the reference value is found
while(less(a[++left],key)){
if (left==hi){
//It has been scanned to the far right. There is no need to continue scanning
break;
}
}
if (left>=right){
//All elements are scanned and the loop ends
break;
}else{
//Swap elements at left and right indexes
exch(a,left,right);
}
}
//Swap the position at the last right index and the index where the reference value is located
exch(a, lo, right);
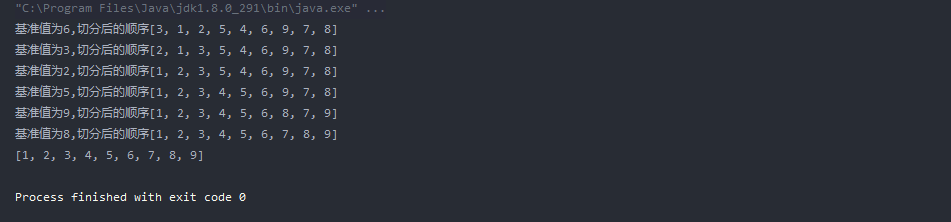
System.out.println("The reference value is"+key+",Order after segmentation"+Arrays.toString(a));
//right is the boundary of segmentation
return right;
}
/**
* Compare element sizes
*/
private static boolean less(Comparable v, Comparable w){
return v.compareTo(w) < 0;
}
/**
* Swap element location
*/
private static void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
}Test code:
public class Test {
public static void main(String[] args) {
Integer[] a = {6, 1, 2, 7, 9, 3, 4, 5, 8};
Quick.sort(a);
System.out.println(Arrays.toString(a));
}
}
Test print results: