Basic learning notes of algorithm toolbox

[excerpt from exercises in the fourth week] close pair of points using divide and conquer algorithm

1. Problem Statement

1.1. Task

In this problem, your goal is to find the closest pair of points in a given point.
This is a basic principle of computational geometry, which is applied in the fields of graphics, computer vision, traffic control system and so on. For example, graphics, computer vision, traffic control system, etc.
Given 𝑛 points on a plane, find the smallest distance between a pair of two (different) points. Recall
that the distance between points ( 𝑥 1 , 𝑦 1 ) (𝑥_1, 𝑦_1) (x1​,y1​) and ( 𝑥 2 , 𝑦 2 ) (𝑥_2, 𝑦_2) (x2​,y2​) is equal to ( 𝑥 1 − 𝑥 2 ) 2 + ( 𝑦 1 − 𝑦 2 ) 2 . \sqrt{(𝑥_1 − 𝑥_2) ^2 + (𝑦_1 − 𝑦_2)^2} . (x1​−x2​)2+(y1​−y2​)2 ​.

1.2. Input Format

The first line contains the number 𝑛 of points. Each of the following 𝑛 lines defines a point ( 𝑥 𝑖 , 𝑦 𝑖 ) (𝑥_𝑖 , 𝑦_𝑖) (xi​,yi​).

1.3. Constraints

2 ≤ 𝑛 ≤ 105 2 ≤ 𝑛 ≤ 105 2≤n≤105; − 109 ≤ 𝑥 𝑖 , 𝑦 𝑖 ≤ 109 −109 ≤ 𝑥_𝑖, 𝑦_𝑖 ≤ 109 −109≤xi​,yi​≤109 are integers.

1.4. Output Format

Output the minimum distance. The absolute value of the difference between the answer
of your program and the optimal value should be at most 1 0 − 3 10^{−3} 10−3. To ensure this, output your answer
with at least four digits after the decimal point (otherwise your answer, while being computed correctly,
can turn out to be wrong because of rounding issues).

2. Brute Force Approach

Checking every possible pair of points; takes quadratic time.
The time complexity of the brute force solution of the nearest coordinate pair problem (i.e. checking each pair of possible coordinates) is O ( n 2 ) O(n^2) O(n2). We need divide and conquer algorithm to solve this problem faster.

#include <algorithm>
#include <iostream>
#include <sstream>
#include <iomanip>
#include <vector>
#include <string>
#include <cmath>

using std::vector;
using std::string;
using std::min;
//define a structure 'coord' to store each pair of point
struct coord {
	int x;
	int y;
}coord_unit;

//the brute force approach
double bruteForce(vector<coord> distance20) {
	double min_dis = 10000000000000.0;
	for (int i = 0; i < distance20.size(); i++) {
		for (int j = i+1; j < distance20.size(); j++) {
			if (find_dist(distance20[i], distance20[j]) < min_dis) {
				min_dis = find_dist(distance20[i], distance20[j]);
			}
		}
		return min_dis;
	}
}
//the main function
int main() {
  size_t n;
  std::cin >> n;
  vector<int> x(n);
  vector<int> y(n);
  for (size_t i = 0; i < n; i++) {
    std::cin >> x[i] >> y[i];
  }
//define a vector distance20 to store the coord pairs
  vector<coord> distance20;
  for (int i = 0; i < x.size(); i++) {
	  coord_unit.x = x[i];
	  coord_unit.y = y[i];
	  distance20.push_back(coord_unit);
  }
  std::cout << std::fixed;
  std::cout << std::setprecision(9) << bruteForce(distance20) << "\n";
}

3. Divide and Conquer Approach

3.1. Closest Pair in the Plane

As shown in the following figure, a point set on a plane is given S S S. We use a vertical line l l l divide it into two subsets S 1 S_1 S1 # and S 2 S_2 S2, so S 1 S_1 The point in S1 ， is l l To the left of l, S 2 S_2 The point in S2 is l l l to the right of the.
Now we solve the problem of these two sets recursively to obtain the minimum distances d1 (for S1) and d2 (for S2). We let d be the minimum.

Now, if the two points with the shortest distance in the whole set are in two subsets respectively, the two points must be in l l l d d Within d. This area is represented as l l l two strips on both sides P 1 P_1 P1 ＾ and P 2 P_2 P2 (as shown).
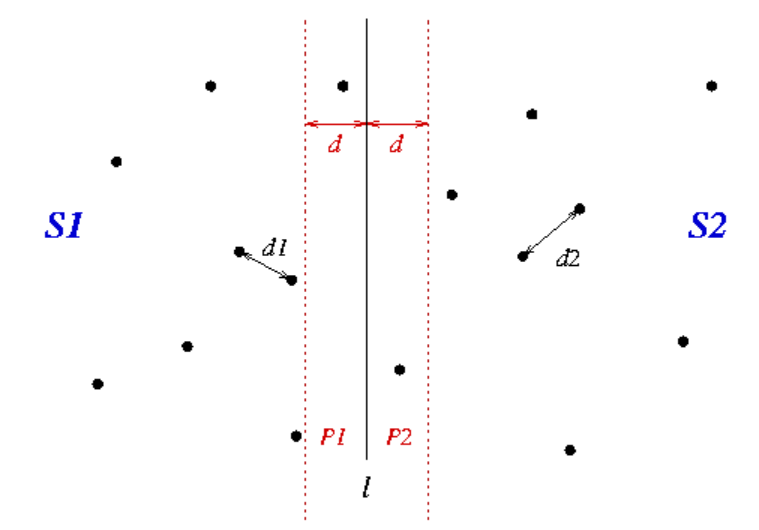Figure 1: schematic diagram of divide and conquer algorithm in two-dimensional plane

We want to make sure P 1 P_1 A point in P1 + P 2 P_2 Is the distance from another point in P2 ？ less than d d d. However, on the plane, all points may be in the strip! This is a disastrous phenomenon because we will have to compare n 2 n^2 n2 to merge this set, so our divide and conquer algorithm will not improve the efficiency!
Fortunately, we observe that for any specific point in a band p p p. Only points in another strip that meet the following constraints need to be checked.

1. In the direction of the other strip, the distance from the point p p p d d Those points within d
2. In the positive and negative y-axis directions, the distance from the point p p p d d Those points within d.

This is because points and points beyond this bounding box p p The distance of p will exceed d d d units (see Figure 3.3). It happens that every point in this box is at least apart d d d. So there can be up to seven points in the box (see the appendix for the proof process). This is good news because we don't need to check all the points now n 2 n^2 n2 points. All we have to do is sort the points in the strip according to the y coordinate, and scan these points in order. Each point is checked with up to 7 adjacent points. This means that up to 7*n comparisons are required to check all candidate pairs.
However, since we sort the points in the strip according to their y coordinates, the process of merging the two subsets is not linear, but actually necessary O ( n l o g n ) O(nlogn) O(nlogn) time.
:
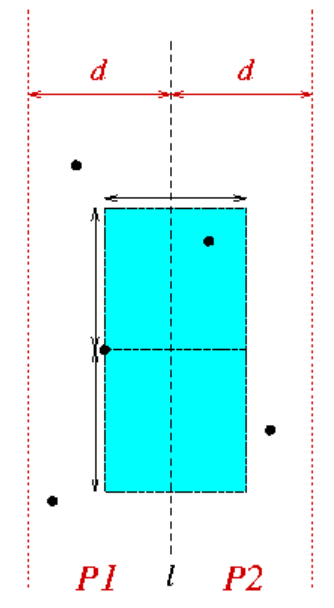Figure 2: the time to find the minimum distance between a point in the strip and other points is constant

3.2. Algorithm and time complexity analysis

1. Through a straight line l l l divide the set into two parts of equal size, and recursively calculate the minimum distance of each part.
2. set up d d d is the minimum of the two minimum distances.
3. Exclude those associated with l l l distance exceeds d d d points.
4. Sort the remaining points according to the Y coordinate
5. Scan the remaining points in the order of y and calculate the distance between each point and its seven neighbors.
6. If any of these distances is less than d, d is updated.

Steps 2-6 define the merging process. Since it is a divide and conquer algorithm, it must be repeated several times.

• Step 2 requires O(1) time
• Step 3 requires O(n) time
• Step 4 is a sort, which requires O(nlogn) time
• Step 5 requires O(n) time (as we saw in the previous section).
• Step 6 requires O(1) time

Therefore, the merging of sub solutions is dominated by the sorting in step 4, so O(nlogn) time is required.
In the divide and conquer algorithm, each level of recursion must be repeated once.

Therefore, the whole ClosestPair algorithm needs O ( l o g n ∗ n l o g n ) = O ( n l o g 2 n ) O(logn*nlogn)=O(nlog2n) O(logn * nlogn) = time of O (nlog2n).
The code is as follows (example):

#include <algorithm>
#include <iostream>
#include <sstream>
#include <iomanip>
#include <vector>
#include <string>
#include <cmath>

using std::vector;
using std::string;
using std::pair;
using std::min;

struct coord {
	int x;
	int y;
}coord_unit;

//coord coord_unit;

bool compare_distance(coord coord1, coord coord2) {
	double d1 =std::sqrt( std::pow(coord1.x, 2) + pow(coord1.y, 2));
	double d2 = std::sqrt(std::pow(coord2.x, 2) + pow(coord2.y, 2));
	return (d1 < d2);
}

bool compare_X(coord coord1, coord coord2) {
	return coord1.x < coord2.x;
}


bool compare_Y(coord coord1, coord coord2) {
	return coord1.y < coord2.y;
}


double find_dist(coord coord1, coord coord2) {
	return (std::sqrt(std::pow((coord1.x - coord2.x), 2) + std::pow((coord1.y - coord2.y), 2)));
}


double bruteForce(vector<coord> distance20) {
	double min_dis = 10000000000000.0;
	for (int i = 0; i < distance20.size(); i++) {
		for (int j = i+1; j < distance20.size(); j++) {
			if (find_dist(distance20[i], distance20[j]) < min_dis) {
				min_dis = find_dist(distance20[i], distance20[j]);
			}
		}
		return min_dis;
	}
}

// A utility function to find the
// distance between the closest points of
// strip of given size. All points in
// strip[] are sorted according to
// y coordinate. They all have an upper
// bound on minimum distance as d.
// Note that this method seems to be
// a O(n^2) method, but it's a O(n)
// method as the inner loop runs at most 6 times
double min_strip(vector<coord> strip, double d) {
	double min = d; // Initialize the minimum distance as d

	std::sort(strip.begin(), strip.end(), compare_Y);
	// Pick all points one by one and try the next points till the difference
	// between y coordinates is smaller than d.
	// This is a proven fact that this loop runs at most 6 times
	for (int i = 0; i < strip.size(); ++i)
		for (int j = i + 1; j < strip.size() && (strip[j].y - strip[i].y) < min; ++j)
			if (find_dist(strip[i], strip[j]) < min)
				min = find_dist(strip[i], strip[j]);

	return min;
}


double minimal_distance(vector<coord> distance20) {

	//base case
	if (distance20.size() < 3) {
		return  bruteForce(distance20);
	}
	//divide
	int mid = distance20.size() / 2; // 7/2 = 3
	vector<coord>::const_iterator first = distance20.begin();
	vector<coord>::const_iterator middle = distance20.begin() + mid;
	vector<coord>::const_iterator last = distance20.end();
	vector<coord> distance_l(first, middle);
	vector<coord> distance_r(middle, last);
	double d1 = minimal_distance(distance_l); // 1, 2, 3
	double dr = minimal_distance(distance_r); // 4, 5, 6, 7

	//conquer
	double d = min(d1, dr);
	vector<coord> mid_strip;
	for (int i = 0; i < distance20.size(); i++) {
		if (abs(distance20[i].x - distance20[mid].x) < d)
			mid_strip.push_back(distance20[i]);
	}
	return min(d, min_strip(mid_strip, d));
}

int main() {
  size_t n;
  std::cin >> n;
  vector<int> x(n);
  vector<int> y(n);
  for (size_t i = 0; i < n; i++) {
    std::cin >> x[i] >> y[i];
  }

  vector<coord> distance20;
  for (int i = 0; i < x.size(); i++) {
	  coord_unit.x = x[i];
	  coord_unit.y = y[i];
	  distance20.push_back(coord_unit);
  }
  std::sort(distance20.begin(), distance20.end(), compare_X);
  std::cout << std::fixed;
  std::cout << std::setprecision(9) << minimal_distance(distance20) << "\n";
}

4. Algorithm improvement

We can slightly improve the algorithm by reducing the time required to implement y-coordinate sorting in step 4. This is done by requiring all points to be pre sorted according to the Y coordinate, so that the sorted array is P y [ ] Py[] Py [], when we make recursive calls, we also need to divide according to the vertical line P y [ ] Py[] Point of Py [].
The recursive solution calculated in step 1 returns points sorted by y coordinates. This will produce two sorted point lists, which can be combined (linear time operation) in step 4 to produce a complete sorted list. Therefore, the revised algorithm involves the following changes:

• Step 0: first, pre sort the set according to the y coordinate to make it a separate array P y [ ] Py[] Py[]
• Step 1: divide the set into two parts of equal size through the straight line l, recursively calculate the distance of each part, pre sort according to the y coordinate, and return the points in each set.
• Step 4: in O ( n ) O( n ) Merge two sort lists into one sort list in O(n) time.

Therefore, the merging process is now dominated by linear time steps, resulting in O ( n l o g n ) O( n log n ) O(nlogn) algorithm is used to find the minimum distance point pair of a group of points in the plane.

4.2. Code (from geeksforgeek)

// A divide and conquer program in C++ to find the smallest distance from a
// given set of points.
  
#include <iostream>
#include <float.h>
#include <stdlib.h>
#include <math.h>
using namespace std;
  
// A structure to represent a Point in 2D plane
struct Point
{
    int x, y;
};
  
  
/* Following two functions are needed for library function qsort().
   Refer: http://www.cplusplus.com/reference/clibrary/cstdlib/qsort/ */
  
// Needed to sort array of points according to X coordinate
int compareX(const void* a, const void* b)
{
    Point *p1 = (Point *)a,  *p2 = (Point *)b;
    return (p1->x - p2->x);
}
// Needed to sort array of points according to Y coordinate
int compareY(const void* a, const void* b)
{
    Point *p1 = (Point *)a,   *p2 = (Point *)b;
    return (p1->y - p2->y);
}
  
// A utility function to find the distance between two points
float dist(Point p1, Point p2)
{
    return sqrt( (p1.x - p2.x)*(p1.x - p2.x) +
                 (p1.y - p2.y)*(p1.y - p2.y)
               );
}
  
// A Brute Force method to return the smallest distance between two points
// in P[] of size n
float bruteForce(Point P[], int n)
{
    float min = FLT_MAX;
    for (int i = 0; i < n; ++i)
        for (int j = i+1; j < n; ++j)
            if (dist(P[i], P[j]) < min)
                min = dist(P[i], P[j]);
    return min;
}
  
// A utility function to find a minimum of two float values
float min(float x, float y)
{
    return (x < y)? x : y;
}
  
  
// A utility function to find the distance between the closest points of
// strip of a given size. All points in strip[] are sorted according to
// y coordinate. They all have an upper bound on minimum distance as d.
// Note that this method seems to be a O(n^2) method, but it's a O(n)
// method as the inner loop runs at most 6 times
float stripClosest(Point strip[], int size, float d)
{
    float min = d;  // Initialize the minimum distance as d
  
    // Pick all points one by one and try the next points till the difference
    // between y coordinates is smaller than d.
    // This is a proven fact that this loop runs at most 6 times
    for (int i = 0; i < size; ++i)
        for (int j = i+1; j < size && (strip[j].y - strip[i].y) < min; ++j)
            if (dist(strip[i],strip[j]) < min)
                min = dist(strip[i], strip[j]);
  
    return min;
}
  
// A recursive function to find the smallest distance. The array Px contains
// all points sorted according to x coordinates and Py contains all points
// sorted according to y coordinates
float closestUtil(Point Px[], Point Py[], int n)
{
    // If there are 2 or 3 points, then use brute force
    if (n <= 3)
        return bruteForce(Px, n);
  
    // Find the middle point
    int mid = n/2;
    Point midPoint = Px[mid];
  
  
    // Divide points in y sorted array around the vertical line.
    // Assumption: All x coordinates are distinct.
    Point Pyl[mid];   // y sorted points on left of vertical line
    Point Pyr[n-mid];  // y sorted points on right of vertical line
    int li = 0, ri = 0;  // indexes of left and right subarrays
    for (int i = 0; i < n; i++)
    {
      if (Py[i].x <= midPoint.x && li<mid)
         Pyl[li++] = Py[i];
      else
         Pyr[ri++] = Py[i];
    }
  
    // Consider the vertical line passing through the middle point
    // calculate the smallest distance dl on left of middle point and
    // dr on right side
    float dl = closestUtil(Px, Pyl, mid);
    float dr = closestUtil(Px + mid, Pyr, n-mid);
  
    // Find the smaller of two distances
    float d = min(dl, dr);
  
    // Build an array strip[] that contains points close (closer than d)
    // to the line passing through the middle point
    Point strip[n];
    int j = 0;
    for (int i = 0; i < n; i++)
        if (abs(Py[i].x - midPoint.x) < d)
            strip[j] = Py[i], j++;
  
    // Find the closest points in strip.  Return the minimum of d and closest
    // distance is strip[]
    return stripClosest(strip, j, d);
}
  
// The main function that finds the smallest distance
// This method mainly uses closestUtil()
float closest(Point P[], int n)
{
    Point Px[n];
    Point Py[n];
    for (int i = 0; i < n; i++)
    {
        Px[i] = P[i];
        Py[i] = P[i];
    }
  
    qsort(Px, n, sizeof(Point), compareX);
    qsort(Py, n, sizeof(Point), compareY);
  
    // Use recursive function closestUtil() to find the smallest distance
    return closestUtil(Px, Py, n);
}
  
// Driver program to test above functions
int main()
{
    Point P[] = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4}};
    int n = sizeof(P) / sizeof(P[0]);
    cout << "The smallest distance is " << closest(P, n);
    return 0;
}

5. Appendix

Certification process:
https://www.cs.mcgill.ca/~cs251/ClosestPair/proofbox.html

Reference link:
3 Closest Pair: A Divide-and-Conquer Approach
geekforgeeks