Chapter 10 greedy algorithm

Greed has no fixed template routine

If we can find out the local optimum and deduce the global optimum, it is greedy; If the local optimum is not found, it is not greedy, but may be a simple simulation.

Greedy algorithm is generally divided into the following four steps:

• The problem is decomposed into several sub problems
• Find the right greedy strategy
• Solve the optimal solution of each subproblem
• Stacking local optimal solutions into global optimal solutions

When you brush questions or interview, you can manually simulate the local optimum and deduce the overall optimum. If you can't think of a counterexample, try greed.

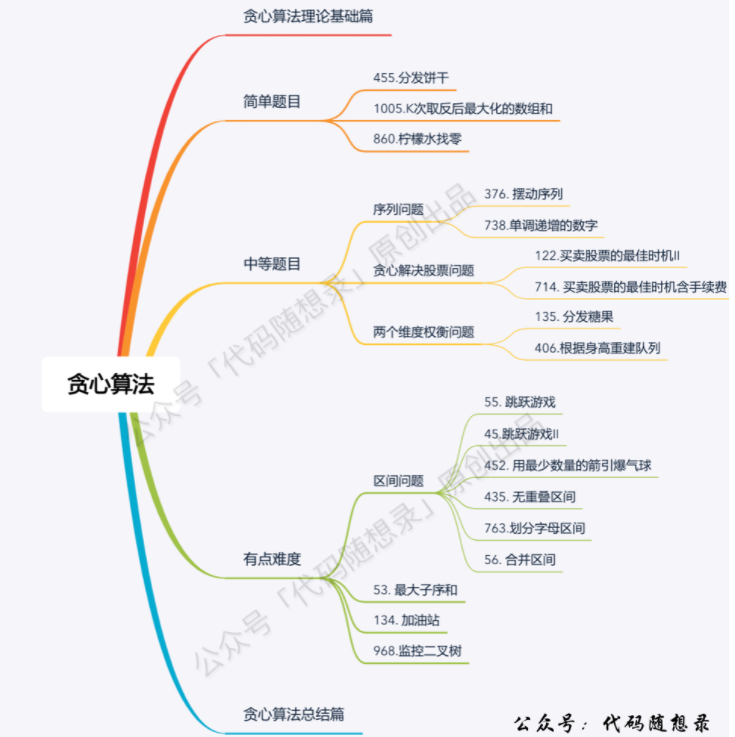
455. Distribution of biscuits [simple]

Idea: small biscuits give small appetite

It can also be reversed. Big biscuits give you a big appetite

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int j = 0;  //Positioning g, i.e. appetite, must be initialized here, or an error will be reported
        for(int i = 0; i < s.size(); i++) {  //Traversal biscuit
            if(j < g.size() && s[i] >= g[j]) {  //The previous judgment condition prevents exceeding the index
                j++;
            }
        }
        return j;   //Index is the number of people
    }
};

376. Swing sequence [medium]

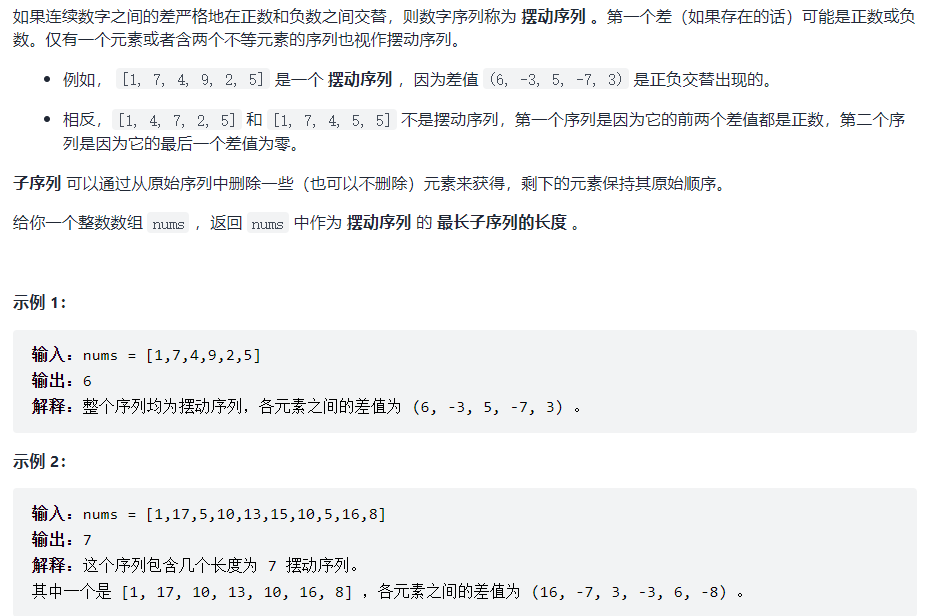
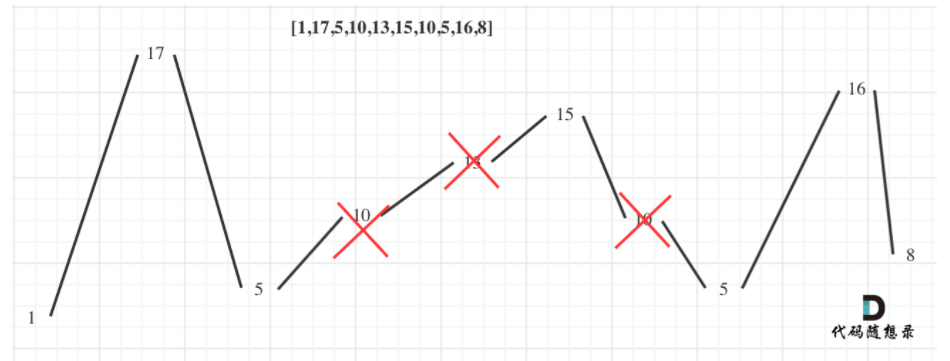
Finding the number of minima

• Idea 1: greed

Time complexity: O(n)

Space complexity: O(1)

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if (nums.size() < 2)   return nums.size();

        int preDiff = nums[1] - nums[0];
        int res = preDiff != 0 ? 2 : 1;
        for(int i = 2; i < nums.size(); ++i){
            int curDiff = nums[i] - nums[i-1];
            //Peak
            if((preDiff<=0 && curDiff>0) || (preDiff>=0 && curDiff<0)){
                res++;
                preDiff = curDiff;
            }
        }
    	return res;
    }
};

Idea 2: dynamic programming

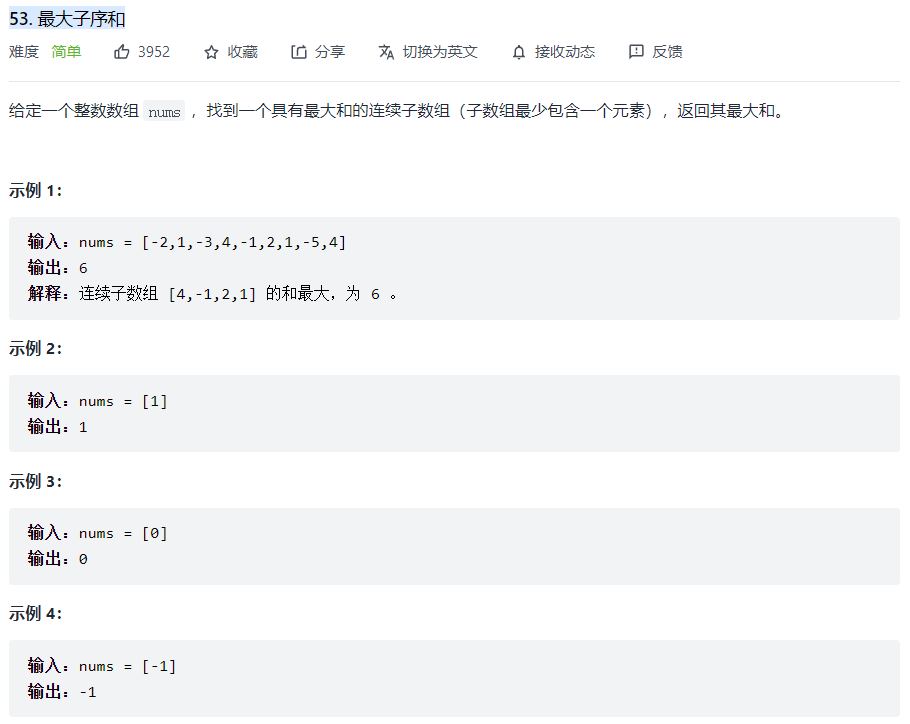
53. Maximum subarray and [simple]

Same title: Sword finger Offer 42 Maximum sum of continuous subarrays

Idea 1: double for loop brute force cracking: calculate the maximum sub order sum from each index

//Two cycle brute for ce cracking
//Calculate the maximum substring starting from index 0, starting from 1, starting from 2
//Time complexity: O(n^2), exceeding the time limit
class Solution
{
public:
    int maxSubArray(vector<int>& nums){
        //Similar to the problem of finding the maximum and minimum value, the initial value must be defined as the theoretical minimum or maximum value
        int sumMax = INT_MIN;
        for (int i = 0; i < nums.size(); i++){
            int sum = 0;
            for (int j = i; j < nums.size(); j++){
                sum += nums[j];
                sumMax = max(sum, sumMax);
            }
        }

        return sumMax;
    }
};

Idea 2: dynamic programming

You can view this person's PPT: https://leetcode-cn.com/problems/maximum-subarray/solution/zui-da-zi-xu-he-cshi-xian-si-chong-jie-fa-bao-li-f/

Time complexity: O(n)

Space complexity: O(n)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {		
		//Update array by replacing elements first
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i - 1] > 0) {          //If the previous element > 0, the latter element is changed to the sum of the two
                nums[i] = nums[i - 1] + nums[i];
            }
        }

		//Then traverse to find the maximum value
        int res = nums[0];
        for (int i : nums) {
            res = max(res, i);
        }

        return res;
    }
};

We can optimize two parallel for loops and solve them with only one for loop

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int res = nums[0];

        for (int i = 1; i < nums.size(); i++) {
            if (nums[i - 1] > 0) {
                nums[i] = nums[i - 1] + nums[i];
            }
            if (nums[i] > res) {
                res = nums[i];
            }
        }

        return res;
    }
};

Then optimize and shorten the code and get close to the official reference answer

• [x]

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int res = nums[0];

        for (int i = 1; i < nums.size(); i++) {
            nums[i] = max(nums[i], nums[i - 1] + nums[i]);  //Mainly this code
            res = max(res, nums[i]);                        //Dynamic recording maximum subsequence sum
        }

        return res;
    }
};

Thoughts on dynamic planning of code Capriccio:

Trilogy:

1. Determine the meaning of dp array (dp table) and subscript
2. Determine recurrence formula
3. How to initialize dp array
4. Determine traversal order
5. Derivation of dp array by example

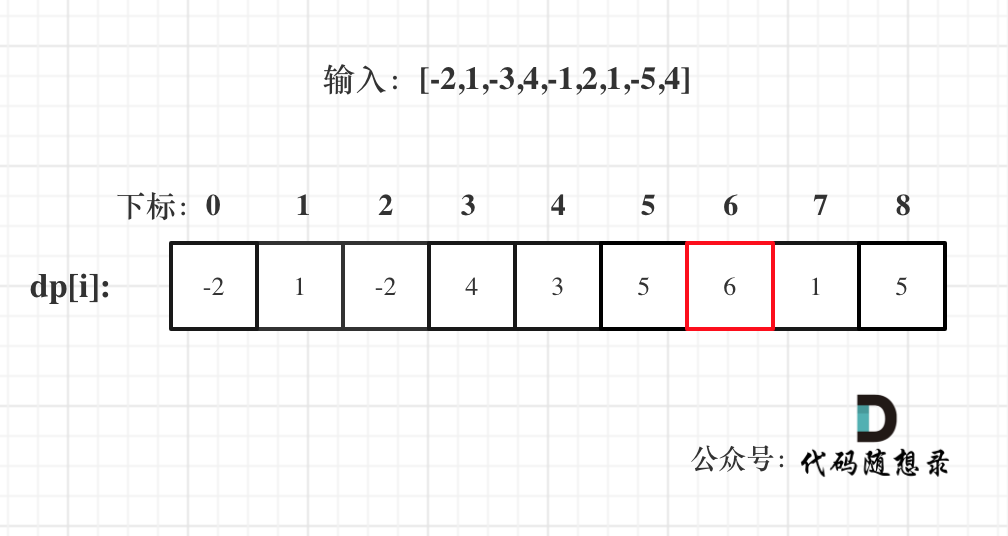
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        int res = dp[0];
        
        for (int i = 1; i < nums.size(); i++) {
            dp[i] = max(dp[i - 1] + nums[i], nums[i]); // State transition formula
            res = max(dp[i], res);                     // Max value of dp[i] saved by res      
        }
        
        return res;
    }
};

• Idea 3: greed

Time complexity: O(n)

Space complexity: O(1)

View ideas: https://leetcode-cn.com/problems/maximum-subarray/solution/dai-ma-sui-xiang-lu-53-zui-da-zi-xu-he-b-8d7l/

Where is greedy?

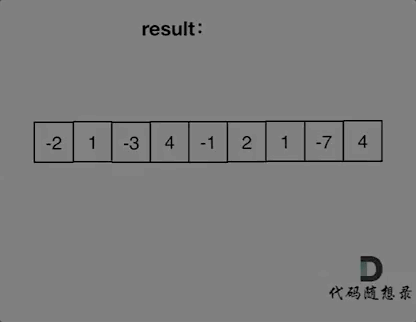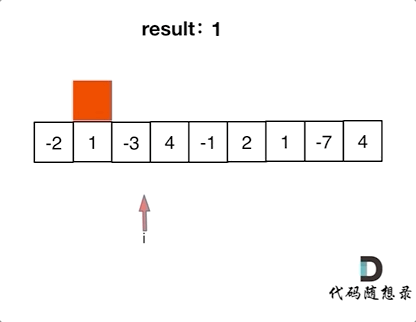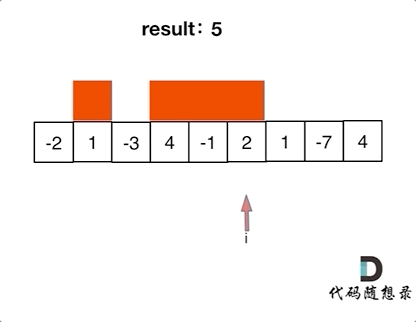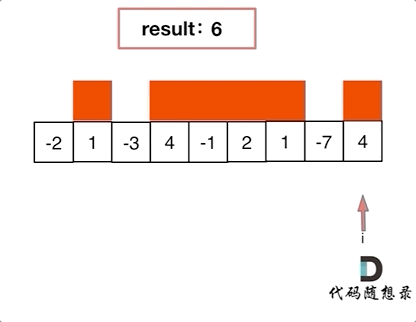
If - 2 and 1 are together, the starting point must be calculated from 1, because negative numbers will only lower the sum, which is the place of greed!

Local optimization: when the current "continuous sum" is negative, give up immediately and recalculate the "continuous sum" from the next element, because the negative number plus the "continuous sum" of the next element will only be smaller and smaller.

Global Optimization: select the maximum "continuous sum"

In the case of local optimization, and record the maximum "continuous sum", the global optimization can be deduced.

class Solution{
public:
    int maxSubArray(vector<int>& nums){
        //Similar to the problem of finding the maximum and minimum value, the initial value must be defined as the theoretical minimum and maximum value
        int res = INT_MIN;
        int sum = 0;
        for (int i = 0; i < nums.size(); i++){
            sum += nums[i];
            res = max(res, sum);
            
            //If sum < 0, start looking for the sub sequence string again
            if (sum < 0){
                sum = 0;
            }
        }

        return res;
    }
};

1005. Maximum array sum after K negations [simple]

class Solution {
public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        int nums_min = INT_MAX;
        int res = 0;
        for(int i = 0; i < nums.size(); i++){
            if(k > 0 && nums[i] < 0){
                nums[i] = -nums[i];
                k--;
            }
            res += nums[i];
            nums_min = min(nums_min, nums[i]);
        }
        
        if(k % 2 == 0) return res;
        else return res - 2*nums_min;
    }
};

• Mainly write absolute value sorting

class Solution {
static bool cmp(int a, int b) {   //Absolute values are sorted from large to small
    return abs(a) > abs(b);
}
    
public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end(), cmp);       // Step 1: sort by absolute value, from large to small
        
        for (int i = 0; i < nums.size(); i++) {    // Step 2: - change+
            if (nums[i] < 0 && k > 0) {
                nums[i] = -nums[i];
                k--;
            }
        }
        
        if (k % 2 == 1)  nums[nums.size() - 1] *= -1; // Step 3: how much is k? See if you need to change the sign of the minimum value
        
        int res = 0;
        for (int num : nums)  res += num;        // Step 4: collect
        return res;
    }
};

134. Gas stations [medium]

Idea 1: violent cracking

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for (int i = 0; i < cost.size(); i++) {
            int rest = gas[i] - cost[i]; // Record the remaining oil
            if (rest < 0)  continue;
            
            int index = (i + 1) % cost.size(); //Index of the next gas station
            while (rest >= 0 && index != i) {  // Simulate driving a circle with i as the starting point
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            
            // If you take i as the starting point and run one lap, the remaining oil quantity > = 0, return to the starting position
            if (rest >= 0 && index == i) return i;
        }
        return -1;
    }
};

Idea 2: greed

• Case 1: if the sum of gas is less than the sum of cost, you can't run a lap no matter where you start
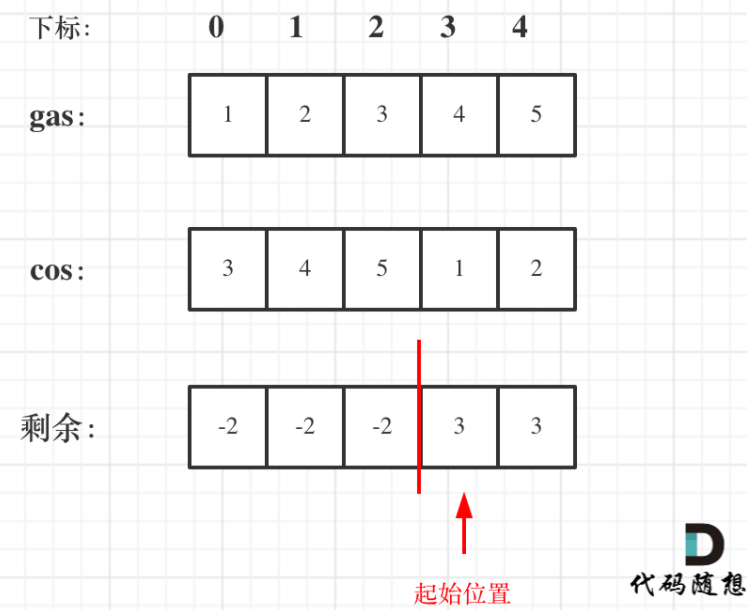
• Case 2: rest[i] = gas[i]-cost[i] is the remaining oil of the day. I is calculated from 0 and accumulated to the last station. If there is no negative number in the accumulation, it means that the oil has not been cut off from 0, so 0 is the starting point.
• Case 3: if the minimum accumulated value is negative, the car should start from the non-0 node. From the back to the front, see which node can fill in the negative number. The node that can fill in the negative number is the starting node.

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int minSum = INT_MAX; // Starting from the starting point, the minimum amount of oil in the tank
        for (int i = 0; i < gas.size(); i++) {
            int rest = gas[i] - cost[i];
            curSum += rest;
            minSum = min(minSum, curSum);
        }
        if (curSum < 0) return -1;  // Case 1
        if (min >= 0) return 0;     // Situation 2
                                    // Situation 3
        for (int i = gas.size() - 1; i >= 0; i--) {
            int rest = gas[i] - cost[i];
            min += rest;
            if (min >= 0) {
                return i;
            }
        }
        return -1;
    }
};

• Idea 3: greedy method 2

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;   //Remaining fuel after full lap
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];   
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // Once the current cumulative rest[i] and curSum are less than 0
                start = i + 1;  // The starting position is updated to i+1
                curSum = 0;     // curSum starts at 0
            }
        }
        
        if (totalSum < 0)    return -1; // It means you can't run a lap
        else return start;
    }
};

860. Lemonade change [simple]

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int money[2] = {0,0};  //Record the number of 5 and 10 yuan notes respectively
        for(auto bill : bills){
            if(bill == 5){
                money[0]++;
            }
            else if(bill == 10){
                money[0]--;
                money[1]++;
                if(money[0] < 0)  return false;
            }
            else if(bill == 20){
                if(money[1] > 0){  //There are 10 yuan bills. One 5 yuan and one 10 yuan change
                    money[1]--;
                    money[0]--;
                }
                else{
                    money[0] -= 3;  //If you don't have 10 yuan, change three pieces of 5 yuan
                }

                if(money[0] < 0)  return false;
            }
        }
        return true;
    }
};

452. Detonate the balloon with a minimum number of arrows [medium]

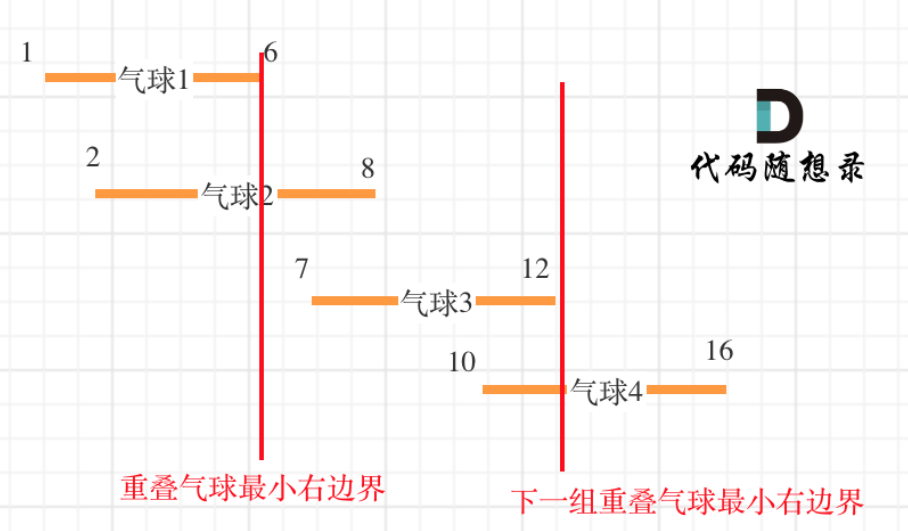
• Sort by left boundary, from small to large

class Solution {
private:
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];
    }
    
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.size() == 0) return 0;
        sort(points.begin(), points.end(), cmp);

        int res = 1; // points is not empty. At least one arrow is required
        for (int i = 1; i < points.size(); i++) { //Two balloons and more running here
            if (points[i][0] > points[i - 1][1]) {  // Balloon i is not next to balloon i-1. Note that this is not >=
                res++; // Need an arrow
            }
            else {  // Balloon i is next to balloon i-1
                points[i][1] = min(points[i - 1][1], points[i][1]); // Update the minimum right boundary key code of overlapping balloon
            }
        }
        
        return res;
    }
};

• Time complexity: O(n\log n), because there is a fast scheduling
• Space complexity: O(1)

435. Non overlapping interval [medium]

Idea: count the number of non overlapping intervals, and then subtract the total number to get the result

Sort by right boundary

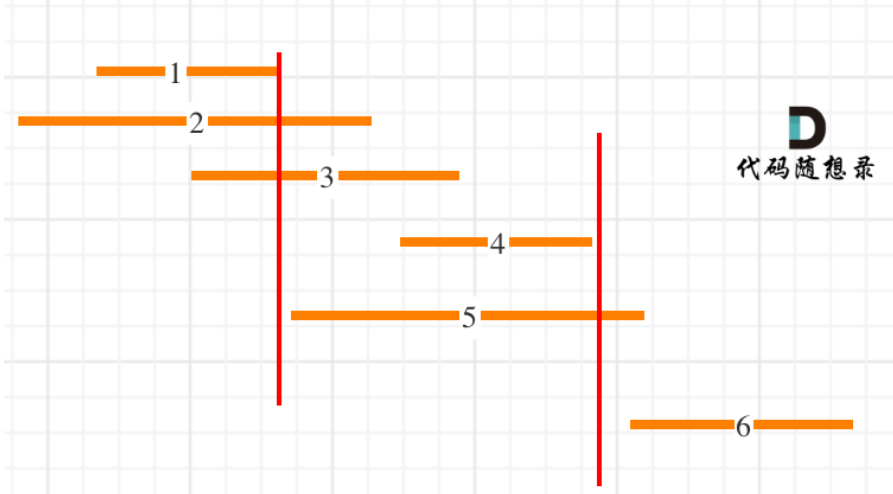
class Solution {
public:
    // Sort according to the right boundary of the interval
    static bool cmp (const vector<int>& a, const vector<int>& b) {
        return a[1] < b[1];
    }
    
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        //if (intervals.size() == 0) return 0;
        sort(intervals.begin(), intervals.end(), cmp);
        
        int count = 1; // Record the number of non intersecting intervals
        int end = intervals[0][1]; // Record interval division point
        for (int i = 1; i < intervals.size(); i++) {  //The calculation has several non overlapping intervals
            if (end <= intervals[i][0]) {
                end = intervals[i][1];
                count++;
            }
        }
        
        return intervals.size() - count;
    }
};

• Time complexity: O(n\log n), with a fast scheduling
• Space complexity: O(1)

763. Division of letter interval [medium]

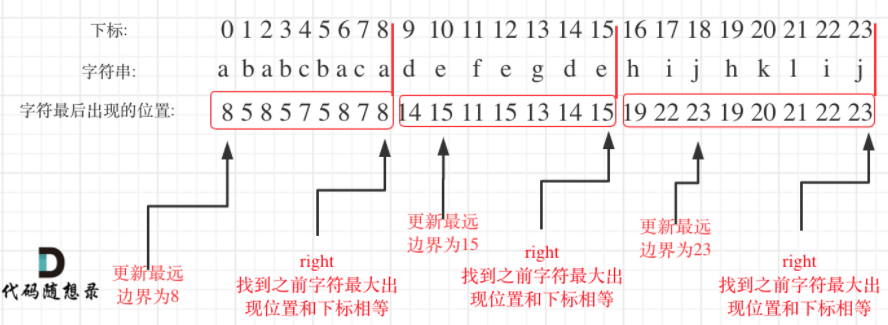
It must be traversed twice: the first traversal updates the index and the second traversal collects the results

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int hash[26] = {0};   //Store the last index corresponding to the character
        for(int i = 0; i < s.size(); i++){  //Count the last position of each character
            hash[s[i] - 'a'] = i;
        }

        int right = 0;   //The start and end indexes of each substring
        int left = 0;
        vector<int> res;
        for(int i = 0; i < s.size(); i++){
            right = max(right, hash[s[right] - 'a']);   // It is important to find the farthest boundary of the character
            if(i == right){
                res.push_back(right - left + 1);
                left = right + 1;
            }
        }

        return res;
    }
};

• Time complexity: O(n)
• Space complexity: O(1). The hash array used is of fixed size

56. Consolidation interval [medium]

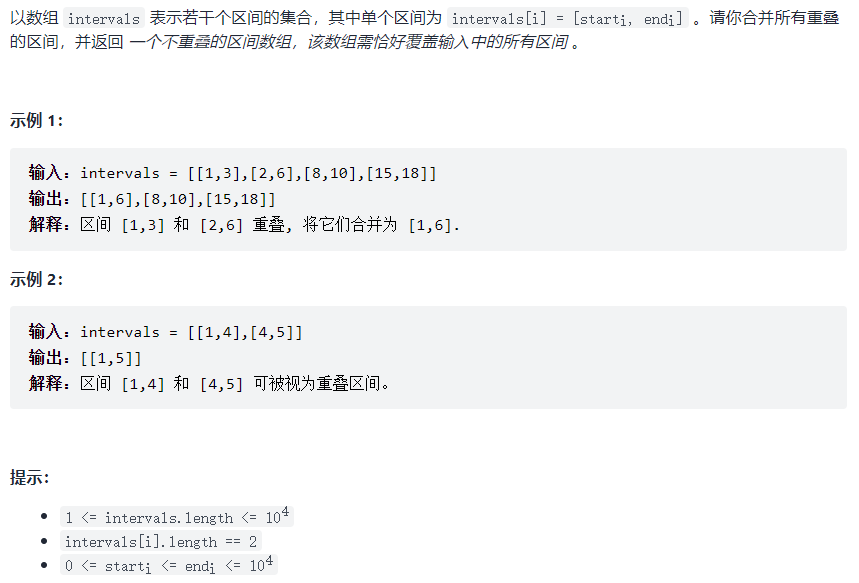
Self written:

class Solution {
public:
    static bool cmp(const vector<int>& a, const vector<int>& b){
        if(a[0] == b[0])  return a[1] < b[1];
        return a[0] < b[0];
    }

    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if(intervals.size() == 1)  return intervals;   //1. Handle the case of size==1
        
        sort(intervals.begin(), intervals.end(), cmp);   //2. Sorting
        
        vector<vector<int>> res;
        for(int i = 1; i < intervals.size(); ++i){
            if(intervals[i][0] <= intervals[i-1][1]){  //Core code
                intervals[i][0] = intervals[i-1][0];
                intervals[i][1] = max(intervals[i-1][1], intervals[i][1]);
                intervals[i-1][1] = -1;
            }
            else{
                res.push_back(intervals[i-1]);
            }
        }
        
        //Process last
        if(intervals[intervals.size()-1][0] > intervals[intervals.size()-2][1]){
            res.push_back(intervals[intervals.size()-1]);
        }

        return res;
    }
};

• Official answer

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if (intervals.size() < 2) return intervals;
        
        // The sorted parameters use lamda expressions
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});
        
        vector<vector<int>> res;
        res.push_back(intervals[0]);
        for (int i = 1; i < intervals.size(); i++) {
            if (res.back()[1] >= intervals[i][0]) { // Merge interval
                res.back()[1] = max(res.back()[1], intervals[i][1]);  //Merge here
            } 
            else {
                res.push_back(intervals[i]);
            }
        }
        
        return res;
    }
};

• Time complexity: O(n\log n), with a fast scheduling
• Space complexity: O(1). I didn't calculate the space occupied by the container of the result array (return value)

738. Monotonically increasing numbers [medium]

Idea 1: violent cracking

Subtract one by one to determine whether the conditions are met

class Solution {
	//brute force   
	//Time complexity: O (nm) m is the digital length of n
	//Space complexity: O(1)
public:
	bool checkNum(int num) {
		int low_pos = 10;  //Record the lowest order

		while (num) {
			int temp_pos = num % 10;  //Take out the lowest position
			if (low_pos >= temp_pos) low_pos = temp_pos;  //The lowest bit is greater than the second lowest bit, and the lowest bit is updated
			else return false;        //If the low bit is smaller than the high bit, false

			num = num / 10;
		}
		return true;
	}

	int monotoneIncreasingDigits(int N) {
		for (int i = N; i > 0; i--) {    //Judge one by one
			if (checkNum(i)) return i;
		}
		return 0;
	}
};

• Idea 2: greed

class Solution {
public:
	int monotoneIncreasingDigits(int N) {
		string strNum = to_string(N);   //Function of converting number to string header file

        //1. Find the mark position and make the previous digit of the mark position - 1
		int flag = strNum.size();
		for (int i = strNum.size() - 1; i > 0; i--) {    //You must traverse from the back to the front, and vice versa
			if (strNum[i - 1] > strNum[i]) {  //Previous > next
				flag = i;                     //The last one is changed to 9
				strNum[i - 1]--;              //Previous digit minus 1 332 - > 322 - > 222
			}
		}

        //2. Mark position change 9
		for (int i = flag; i < strNum.size(); i++) {  //Mark position starts to change 9
			strNum[i] = '9';        //222 -> 299
		}

		return stoi(strNum);  //String to number
	}
};

• Time complexity: O(n), n is the number length
• Spatial complexity: O(n), which requires a string. It is more convenient to convert it into a string

968. Monitoring binary tree [difficult, no]

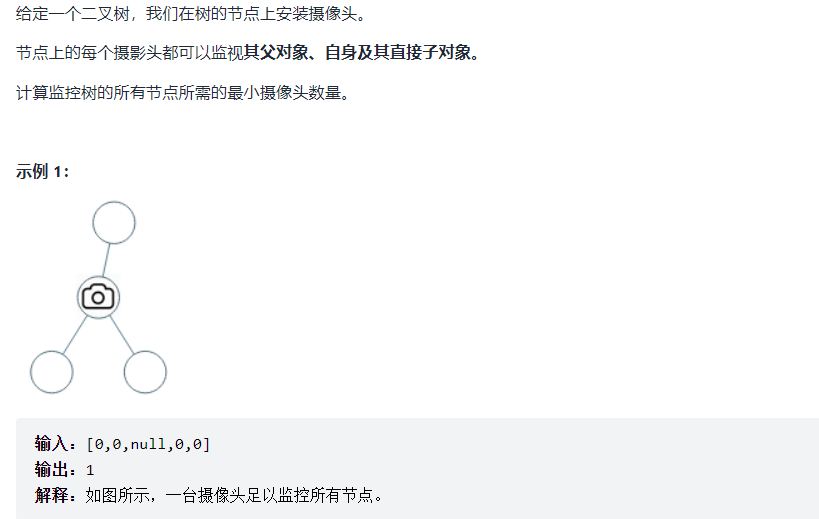
There are three types:

• This node has no coverage
• This node has cameras
• This node has overrides

We have three numbers:

• 0: this node has no overrides
• 1: This node has cameras
• 2: This node has overrides

You can use post order traversal, that is, the order in the left and right, so that you can deduce from bottom to top in the process of backtracking.

Single layer logic processing mainly includes the following four types:

• Case 1: the left and right nodes are covered
  • If the left child has coverage and the right child has coverage, then the intermediate node should be in the state of no coverage.
• Case 2: at least one of the left and right nodes has no coverage
  • In the following cases, the intermediate node (parent node) should place the camera
• Case 3: at least one of the left and right nodes has a camera
  • In the following cases, if one of the left and right child nodes has a camera, its parent node should be 2 (covered state)
• Case 4: the header node is not covered

// Version one
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {

        // Empty node, which has coverage
        if (cur == NULL) return 2;

        int left = traversal(cur->left);    // Left
        int right = traversal(cur->right);  // right

        // Case 1
        // Both left and right nodes are covered
        if (left == 2 && right == 2) return 0;

        // Situation 2
        // Left = = 0 & & right = = no coverage for nodes around 0
        // Left = = 1 & & right = = 0 the left node has a camera and the right node has no coverage
        // Left = = 0 & & right = = 1 whether the left node is covered, and whether the right node is covered
        // Left = = 0 & & right = = 2 left node not covered, right node covered
        // Left = = 2 & & right = = 0 the left node is covered, and the right node is not covered
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }

        // Situation 3
        // Left = = 1 & & right = = 2 the left node has a camera and the right node has coverage
        // Left = = 2 & & right = = 1 left node has coverage and right node has camera
        // Left = = 1 & & right = = 1 there are cameras on the left and right nodes
        // In other cases, the previous code has been overwritten
        if (left == 1 || right == 1) return 2;

        // I didn't use else in the above code, mainly to show the conditions of each branch, so that the code is helpful for readers to understand
        // This return -1 logic will not come here.
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // Situation 4
        if (traversal(root) == 0) { // root no overwrite
            result++;
        }
        return result;
    }
};

Jumping game

55. Jumping game [medium]

class Solution {
public:
    bool canJump(vector<int>& nums) {
        if (nums.size() < 2) return true;  // Only 0,1 elements can be achieved
        
        int cover = 0;
        for (int i = 0; i < nums.size(); i++) { 
            if(i <= cover){                       //i within coverage
                cover = max(i + nums[i], cover);  //Update coverage
                if (cover >= nums.size() - 1) return true; // It indicates that the end point can be covered
            }
            else   return false;
        }
        
        return false;  //This sentence can't go
    }
};

45. Jumping game II [medium]

The least number of times to reach the last position, assuming that you can always reach the last position

It can be seen from the figure that when the moving subscript reaches the longest subscript covered by the current, the number of steps should be increased by one to increase the coverage distance. The final number of steps is the minimum number of steps.

There is a special case to consider here. When the mobile subscript reaches the longest range subscript currently covered

• If the current longest covered subscript is not the end of the set, the number of steps will be increased by one and you need to continue.
• If the current longest covering subscript is the end of the set, you don't need to add one step because you can't go back.

class Solution {
public:
    int jump(vector<int>& nums) {
        if (nums.size() < 2) return 0;
        
        int curDistance = 0;    // Current coverage longest subscript
        int ans = 0;            // Record the maximum number of steps taken
        int nextDistance = 0;   // Next, cover the longest subscript
        
        for (int i = 0; i < nums.size(); i++) {
            nextDistance = max(nums[i] + i, nextDistance);  // Record the longest subscript covered in the next step
            if (i == curDistance) {                        // Encountered the longest subscript of current coverage
                if (curDistance < nums.size() - 1) {       // If the current covering longest distance subscript is not the end point
                    ans++;                                 // Need to take the next step
                    curDistance = nextDistance;            // Update the longest distance subscript of current coverage (equivalent to refueling)
                    if (nextDistance >= nums.size() - 1) break; // The coverage of the next step can reach the end point and end the cycle
                } 
                else break;     // At present, the longest distance subscript covered is the end of the set. There is no need to do ans + + operation, and it will end directly
            }
        }
        return ans;
    }
};

When traversing the array, we do not access the last element, because before accessing the last element, our boundary must be greater than or equal to the last position, otherwise we cannot jump to the last position. If we access the last element, when the boundary is exactly the last position, we will increase the "number of unnecessary jumps", so we don't have to access the last element.

• [x]

class Solution {
public:
    int jump(vector<int>& nums) {
        int curDistance = 0;    // The longest subscript currently covered
        int ans = 0;            // Record the maximum number of steps taken
        int nextDistance = 0;   // The longest subscript covered in the next step
        for (int i = 0; i < nums.size() - 1; i++) { // Note that this is less than num Size () - 1, this is the key
            nextDistance = max(nums[i] + i, nextDistance); // Record the longest subscript covered in the next step
            if (i == curDistance) {                 // Encountered the longest subscript of the current coverage
                curDistance = nextDistance;         // Update the longest subscript of the current overlay
                ans++;
            }
        }
        return ans;
    }
};

Two dimensional trade-off problem

135. Distribution of candy [difficulties]

• Idea 1: greed

Time complexity: O(n)

Space complexity: O(n)

Two traversals, one backward and one forward

class Solution {
public:
    int candy(vector<int>& ratings) {
        //1. Distribute candy
        vector<int> candyVec(ratings.size(), 1);  //1.1 one for each person first
        // Front back
        for (int i = 1; i < ratings.size(); i++) {       
            if (ratings[i] > ratings[i - 1]) {   //1.2 there is one more on the right than on the left
                candyVec[i] = candyVec[i - 1] + 1;
            }
        }
        // From back to front
        for (int i = ratings.size() - 2; i >= 0; i--) {  //Make sure left > right
            if (ratings[i] > ratings[i + 1] ) {
                candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);  //max is selected because you want to keep the above unchanged
            }
        }
        
        // 2. Statistical results
        int res = 0;
        for (int i = 0; i < candyVec.size(); i++) {
            res += candyVec[i];
        }
        return res;
    }
};

Method 2: constant space traversal

Time complexity: O(n)

Space complexity: O(1)

https://leetcode-cn.com/problems/candy/solution/fen-fa-tang-guo-by-leetcode-solution-f01p/

class Solution {
public:
    int candy(vector<int>& ratings) {
        int res = 1;
        int inc = 1;  //Last increment sequence length
        int dec = 0;  //Current decrement sequence length
        int pre = 1;  //The number of apples of the former student
        for (int i = 1; i < ratings.size(); i++) {
            if (ratings[i] >= ratings[i - 1]) {
                dec = 0;
                pre = (ratings[i] == ratings[i - 1]) ? 1 : pre + 1;
                res += pre;
                inc = pre;
            } 
            else {
                dec++;
                if (dec == inc) {
                    dec++;
                }
                res += dec;
                pre = 1;
            }
        }
        
        return res;
    }
};

406. The cohort was reconstructed according to height [medium]

Idea: sort first, then insert

Insertion process:

• Insert [7,0]: [[7,0]]

• Insert [7,1]: [[7,0], [7,1]]

• Insert [6,1]: [[7,0], [6,1], [7,1]]

• Insert [5,0]: [[5,0], [7,0], [6,1], [7,1]]

• Insert [5,2]: [[5,0], [7,0], [5,2], [6,1], [7,1]]

• Insert [4,4]: [[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

• Time complexity: O(n\log n + n^2)

• Space complexity: O(n)

class Solution {
public:
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);   //1. Sort high - > low
        
        vector<vector<int>> que;
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1];
            que.insert(que.begin() + position, people[i]);  //2. Insertion sequence
        }
        
        return que;
    }
};

However, using vector is very time-consuming. In C + +, if the inserted element of vector (which can be understood as a dynamic array and the bottom layer is implemented by an ordinary array) is larger than the size of the ordinary array in advance, there will be an expansion operation at the bottom of vector, that is, apply for twice the size of the original ordinary array, and then copy the data to another larger array.

• [x]

class Solution {
public:
    // Height from big to small row (stand in front of the same k small height)
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        
        list<vector<int>> que; // The bottom layer of list is the implementation of linked list, and the insertion efficiency is much higher than that of vector
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1]; // Insert into position with subscript position
            list<vector<int>>::iterator it = que.begin();
            while (position--) { // Find where to insert
                it++;
            }
            que.insert(it, people[i]);  //The insertion speed of linked list is fast
        }
        
        return vector<vector<int>>(que.begin(), que.end());  //list container - > vector container
    }
};

This method is faster, but it trades space for time

The bottom layer of the dynamic array will be fully copied and expanded, so it takes time

Stock series

121. The best time to buy and sell stocks [simple]

Same title: Sword finger Offer 63 Maximum profit of stock

Can only buy once, sell once, maximum profit

Idea 1: double for brute force cracking; Ideas and The maximal suborder and are very similar

Time complexity: O(n^2)

Space complexity: O(1)

class Solution {
public:
	//Double for loop brute force cracking exceeds the time limit
	int maxProfit(vector<int>& prices) {
		int max_fit = 0;
		for (int i = 0; i < prices.size(); i++) {   
			for (int j = i + 1; j < prices.size(); j++) {
				max_fit = max(max_fit, prices[j] - prices[i]);
			}
		}

		return max_fit;
	}
};

• Idea 2: greed

Stock, go to the minimum value on the left and the maximum value on the right of the array. The difference is the maximum profit

Time complexity: O(n) one for loop traversal

Space complexity: O(1)

Ideas can be viewed from the code Capriccio: https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/solution/dai-ma-sui-xiang-lu-121-mai-mai-gu-piao-odhle/

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int low = INT_MAX;
        int res = 0;
        for (int i = 0; i < prices.size(); i++) {   //Traverse from left to right
            low = min(low, prices[i]);              // Dynamic update minimum price
            res = max(res, prices[i] - low);     // Dynamic update maximum profit
        }
        return res;
    }
};

Idea 3: dynamic programming

It's a little difficult. I'll add it next time

122. The best time to buy and sell stocks II [medium]

Title Meaning:

• Only one stock!
• At present, there are only stock buying or stock buying operations

Idea: draw the stock price of each question into a broken line chart to find the accumulation of all rising segments; Reference 376 questions

• Greed:

Time complexity: O(n)

Space complexity: O(1)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
		for(int i = 1; i < prices.size(); i++){
            res += max(0, prices[i]-prices[i-1]);
        }
        return res;
    }
};

714. The best time to buy and sell stocks includes handling fees [medium, no]

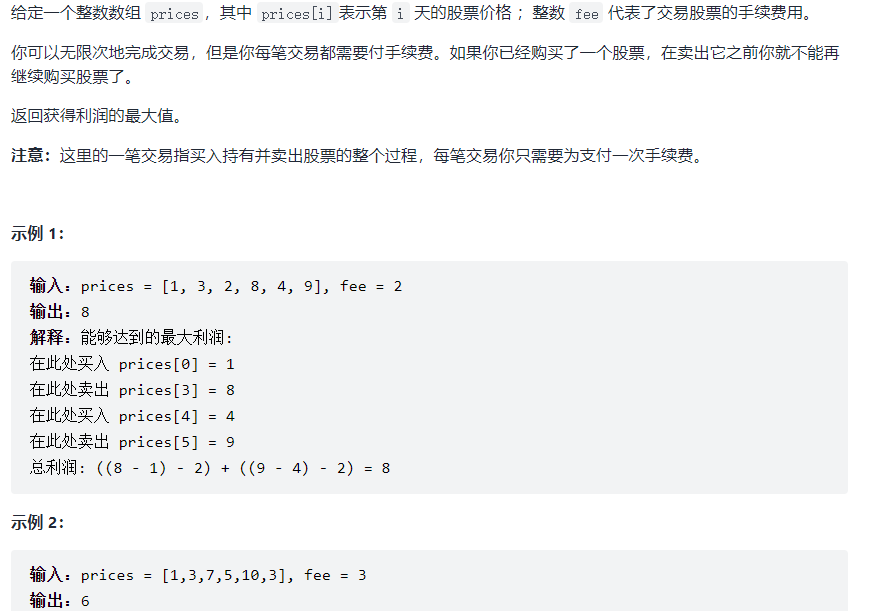
• Idea 1: greed

• Time complexity: O(n)

• Space complexity: O(1)

There are actually three situations when we harvest profits:

• Situation 1: the day of profit harvest is not the last day in the profit range (not really selling, equivalent to holding stocks), so we should continue to harvest profits later.
• Situation 2: the previous day was the last day in the profit range (equivalent to the real sale), and the minimum price should be recorded again today.
• Situation 3: do not operate and keep the original state (buy, sell, do not buy, do not sell)

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int res = 0;
        int minPrice = prices[0]; // Record the lowest price
        for (int i = 1; i < prices.size(); i++) {
            // Case 2: equivalent to buying
            if (prices[i] < minPrice)  minPrice = prices[i];

            // Situation 3: keep the original state (because buying is not cheap at this time, and selling is at a loss)
            //if (prices[i] >= minPrice && prices[i] <= minPrice + fee) {
            //    continue;
            //}

            // To calculate the profit, there may be many times to calculate the profit, and the last time to calculate the profit is the real meaning of selling
            if (prices[i] > minPrice + fee) {
                res += prices[i] - minPrice - fee;
                minPrice = prices[i] - fee; // Situation one, this step is critical
            }
        }
        return res;
    }
};

When we sell a stock, we immediately get the right to buy a stock at the same price without handling charges

• [x]

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int buy = prices[0] + fee;
        int profit = 0;
        for (int i = 1; i < prices.size(); ++i) {
            if (prices[i] + fee < buy) {   //Update purchase price
                buy = prices[i] + fee;
            }
            else if (prices[i] > buy) {    //Collect profits
                profit += prices[i] - buy;
                buy = prices[i];
            }
        }
        return profit;
    }
};

Idea 2: dynamic programming