236. Nearest common ancestor of binary tree
Title Description:

Train of thought analysis:
Anyway, I'm still confused about recursion... More practice can only be. The thought of boss Carl can still be understood. It's really unexpected when he did it himself.
The code is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//We call the current method as a recursive function (post order traversal)
//As soon as the method comes in, we judge whether it is p and q we want, or null
//If it is one of these cases, we will return the current result upward
if(root == p || root == q || root == null) return root;
//Recursively look up the left tree and receive the result with a left pointer
TreeNode left = lowestCommonAncestor(root.left,p,q);
//Recursively look up the right tree and receive the result with a right pointer
TreeNode right = lowestCommonAncestor(root.right,p,q);
//If left and right are not empty, it means that the current node is the nearest common ancestor traced back
if(left != null && right != null) return root;
//If left is empty and right is not empty, it means it is found in the right tree
//vice versa
if(left == null && right != null) return right;
else if(left != null && right == null) return left;
else {//If both are empty, it means that the nearest common ancestor has not been found
return null;
}
}
}
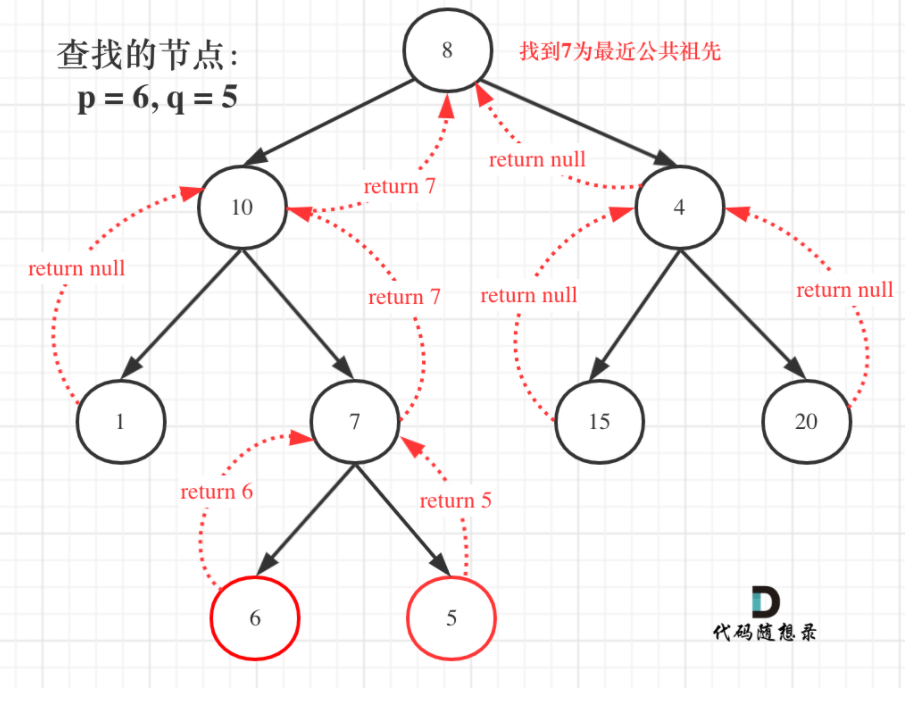
235. Nearest common ancestor of binary search tree
Title Description:
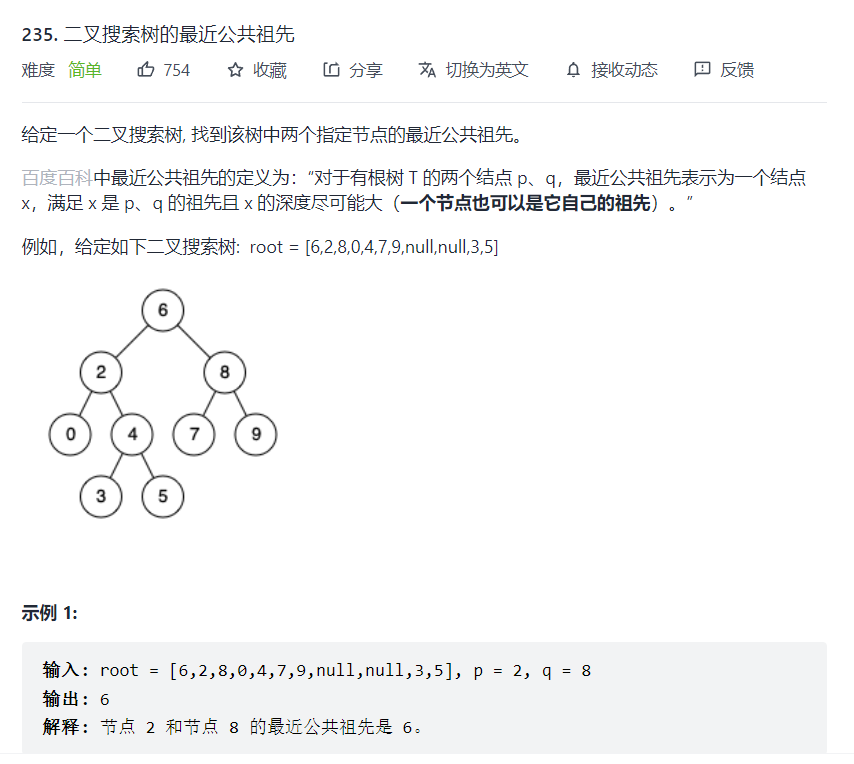
Train of thought analysis:
The binary search tree is also a binary tree, so we can use the backtracking solution of the binary search tree just now. It's the same:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
//This can also be done according to the practice of ordinary binary tree
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == p || root == q || root == null) return root;
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left != null && right != null) return root;
if(left != null && right == null) return left;
else if(left == null && right != null) return right;
else return null;
}
}
However, because it is a binary search tree BST, we can also have another solution, which is to use the characteristic that the left tree is smaller than the root node and the right tree is larger than the root node. When the values of p and q nodes are less than the value of the current root node, we will traverse the left tree to find the nearest public node, otherwise, we can search to the right. If the values of p and q nodes are greater than the value of the current node, it means that they are the nearest public node and directly return the result. The recursive method is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//Directly return the result of recursive function
return fun(root,p,q);
}
//Recursive function
public TreeNode fun(TreeNode root,TreeNode p,TreeNode q){
//If you enter, it will be judged as empty. If root is empty, it will directly return null
if(root == null) return null;
//Because the binary search tree is ordered, we can carry out unilateral recursion according to this feature
//If the current node value is greater than the values of p and q, we will recurse to the left
if(root.val > p.val && root.val > q.val){
TreeNode left = fun(root.left,p,q);
//If left is not empty, you can return the answer directly
if(left != null) return left;
}
//If the current node value is less than the values of p and q, we will recurse to the right
if(root.val < p.val && root.val < q.val){
TreeNode right = fun(root.right,p,q);
//If right is not empty, we can return the answer directly if we find it
if(right != null) return right;
}
//If neither of the above conditions is satisfied
//This indicates that the value of the pq node and the value of the current node root are larger or smaller
//In this case, pq one is in the left subtree and the other is in the right subtree
//Then the current node must be the nearest public ancestor
//Directly return to the current node root
return root;
}
}
The iterative method is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//Because the topic says that pq nodes must exist, so there must be public ancestors recently
//Therefore, we do not need to judge whether the left and right nodes are empty
//Because we can find the answer before we meet the empty node
while(true){
//The values of p and q are less than the value of the current node root
if(root.val > p.val && root.val > q.val){
//So let's iterate to the left
root = root.left;
}else if(root.val < p.val && root.val < q.val){
root = root.right;
}else {//If there is only one large and one small case left, the current node is the nearest common ancestor
//Terminate cycle
break;
}
}
//Returns the current node as the answer
return root;
}
}
701. Insert operation in binary search tree
Title Description:
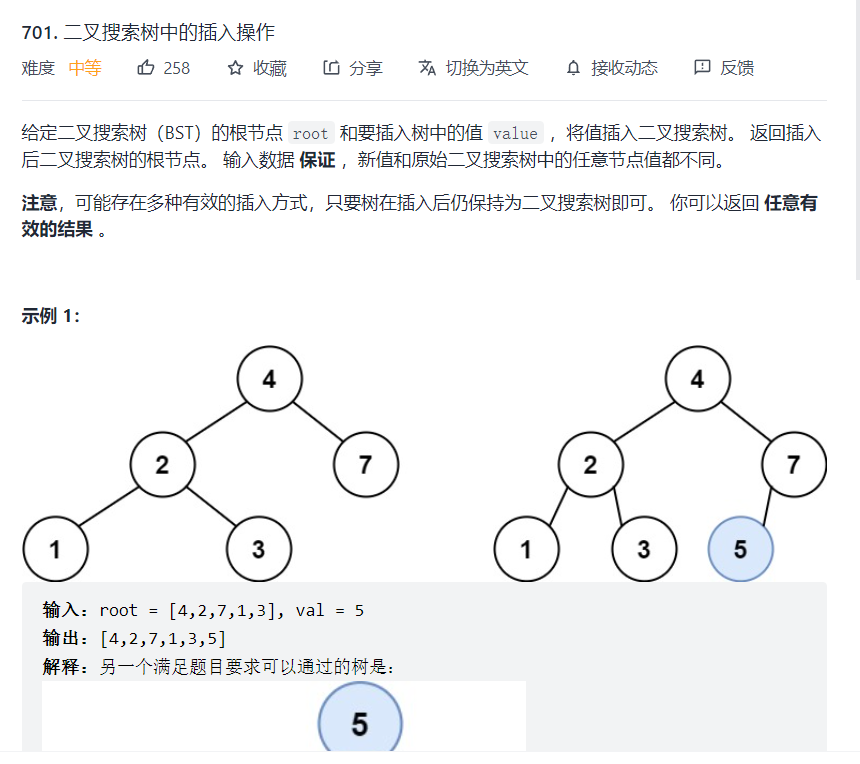
Train of thought analysis:
We can redraw (construct) the binary tree, and then insert the value we want to insert when we encounter an empty node (hanging at the end is the most convenient method). It will be easier to understand the specific code.
The code is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
//According to the characteristics of binary search tree
//It's kind of like reconstructing this binary tree once
//If a null value is encountered during construction, the upward return will be inserted into the
//Hanging in the newly reconstructed binary tree
if(root == null){
TreeNode node = new TreeNode(val);
return node;
}
//If the current node value is greater than the inserted value, recurse to the left
if(root.val > val) root.left = insertIntoBST(root.left,val);
//If the current node value is less than the inserted value, recurse to the right
if(root.val < val) root.right = insertIntoBST(root.right,val);
//Returns the current node
return root;
}
}
450. Delete nodes in binary search tree
Title Description:
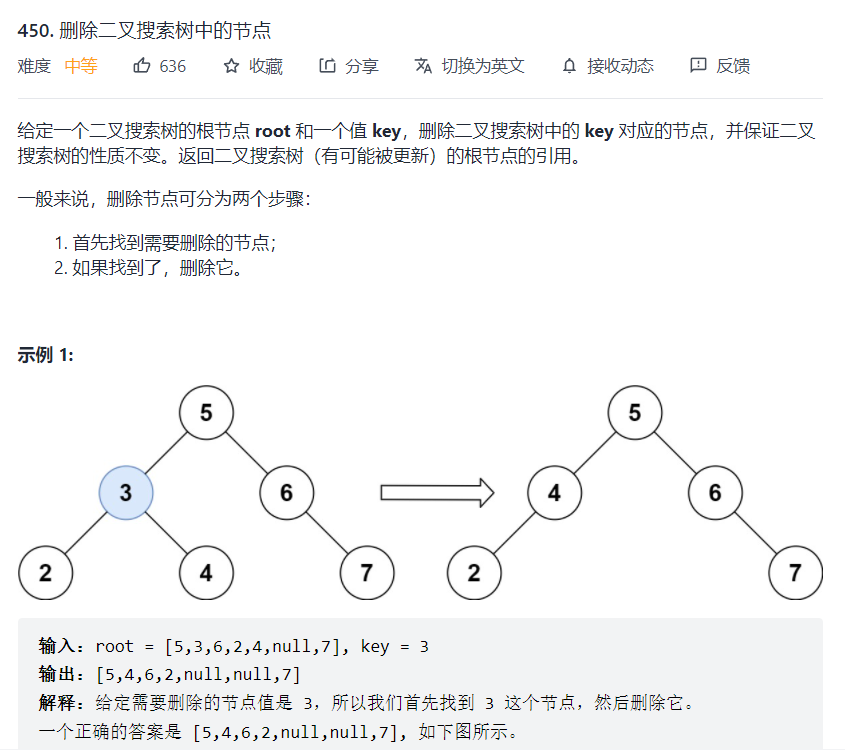
Train of thought analysis:
Boss Carl said it in detail. Just look at it. The comments in my code are also very clear.
The code is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
//Air judgment
if(root == null) return null;
//If the value of the current node is equal to the value of the node to be deleted
if(root.val == key){
//If the left subtree of the current node is empty, we return the right subtree to the upper layer
//In this way, when the upper function reconstructs the binary tree, it will directly hang a tree
if(root.left == null) return root.right;
//If the right subtree of the current node is empty, we return the left subtree to the upper layer
else if(root.right == null) return root.left;
//Otherwise, the left and right subtrees are not empty
else{
//Record the right subtree of the current node with cur pointer
TreeNode cur = root.right;
//Loop through the leftmost leaf node of the right subtree of the current node
//Because you have to hang a subtree up when you go back
while(cur.left != null){
cur = cur.left;
}
//Then we hang the left tree of the current node to the right tree of the current node
//At the bottom of the left (combined with the moving picture of boss Carl)
cur.left = root.left;
//Finally, let the current node point to its right tree
root = root.right;
//Return the current node, and then the upper function will hang it in the
//We are on the regenerated tree
return root;
}
}
//The following is the case of not equal to, so you can continue recursive processing
//If the value of the current node is greater than the target deletion value, the left recursive deletion is performed
if(root.val > key) root.left = deleteNode(root.left,key);
//If the value of the current node is less than the target deletion value, right recursive deletion is performed
if(root.val < key) root.right = deleteNode(root.right,key);
//Return the current node, and the upper function is also used to hang on the tree
//The last returned node is the root node of the new tree we reconstructed
return root;
}
}
669. Pruning binary search tree
Title Description:

Train of thought analysis:
You can understand it by reading the code.
The code is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
//Air judgment
if(root == null) return null;
//The following two IFS are equivalent to deleting nodes that do not meet the requirements
//If the value of the current node is less than low, it will recursively search the right tree with large value
if(root.val < low){
//Because there may be qualified values in the right subtree of the current node, we have to get them in
return trimBST(root.right,low,high);
}
//If the value of the current node is greater than high, the left tree with smaller value will be searched recursively
if(root.val > high){
//Because the left subtree of the current node may have values that meet the conditions, we have to get them in
return trimBST(root.left,low,high);
}
//Processing normal nodes
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
//Return the current node to the previous function call and hang it on the new tree
return root;
}
}
108. Convert an ordered array into a binary search tree
Title Description:
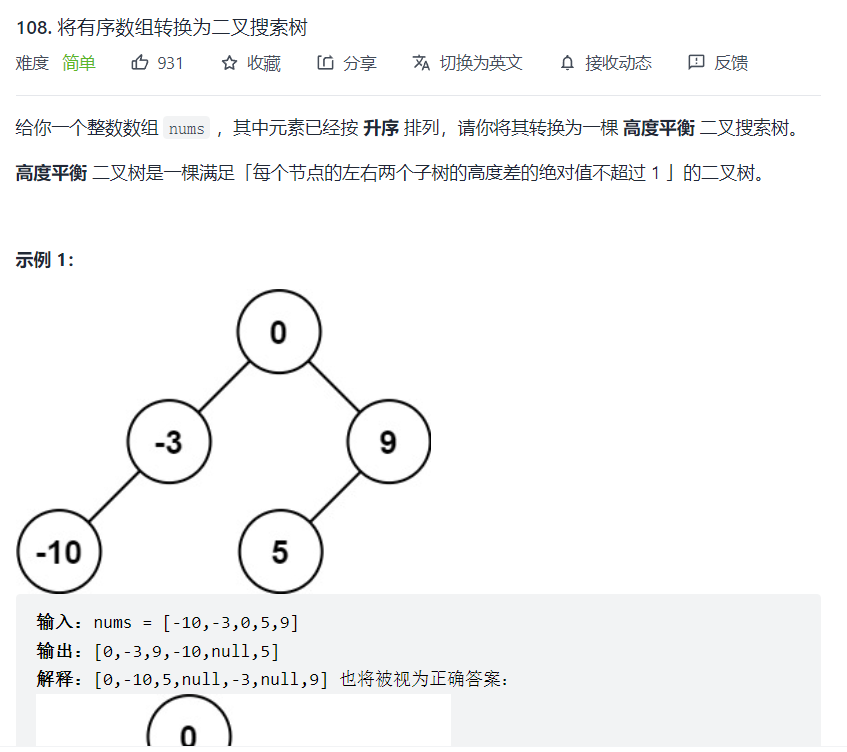
Train of thought analysis:
You can understand it by reading the code. In fact, it is very similar to the previous topic and the implementation method is very similar.
The code is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
//Do it recursively according to the rules of middle order traversal
return fun(nums,0,nums.length-1);//Generally, the array length is - 1, and the same is true for bisection
}
//Recursive function
public TreeNode fun(int[] nums,int left,int right){
//If the array has no value, terminate and return null directly
if(left > right) return null;
//Take the intermediate value
//The following mid writing method can avoid array out of bounds
int mid = left + ((right - left) / 2);
//Create root node
TreeNode root = new TreeNode(nums[mid]);
//Then recurse to the left
root.left = fun(nums,left,mid-1);
//Recursion to the right
root.right = fun(nums,mid+1,right);
//Return the created node to the upper function for mounting
return root;
}
}
538. Convert binary search tree into cumulative tree
Title Description:
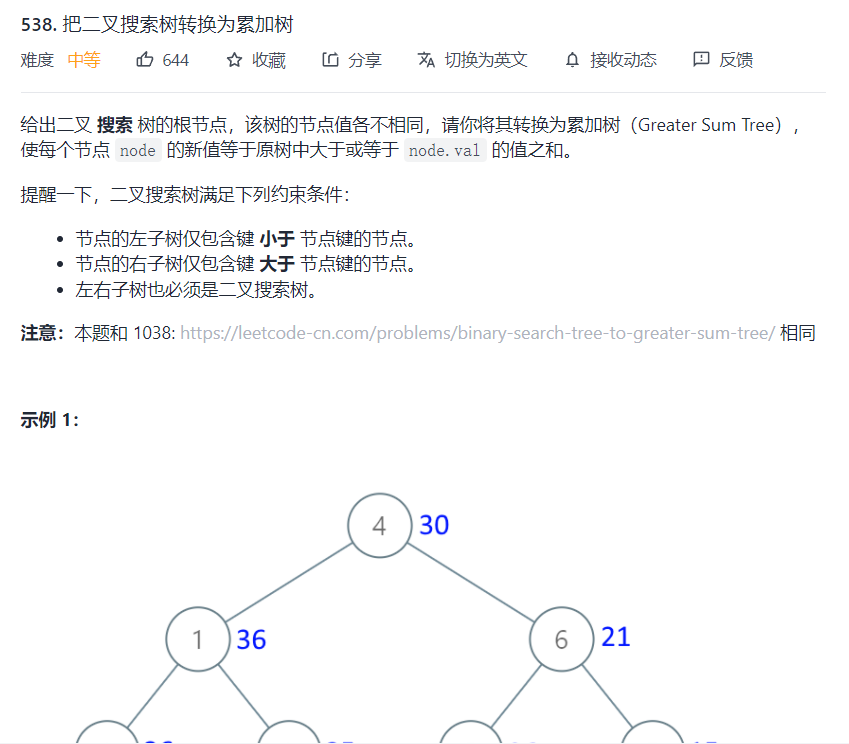
Train of thought analysis:
The meaning of the question is a little confused to tell the truth. In fact, it can be understood from another point of view. It is to get the order after the middle order traversal, and then accumulate the node value in reverse and assign it to the original node.
The idea is summarized as follows: traverse the BST in reverse middle order, then accumulate the values of each node with a global variable, and then re assign the value to the node.
The code is as follows:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
//To tell you the truth, I'm a little confused
//It is to get the order after the middle order traversal, and then accumulate the node value in reverse and assign it to the original node
//Idea: traverse the BST in reverse order, and then use a global variable to accumulate the values of each node, and then assign a new value to the node
int sum;
public TreeNode convertBST(TreeNode root) {
//The reverse middle order is traversed in the order of right, middle and left
//Initialize sum
sum = 0;
//Call recursive function
fun(root);
//Returns the root of the tree
return root;
}
//Recursive function
public void fun(TreeNode root){
//If it is blank, because there is no return value, the function can be terminated directly if it is blank
if(root == null) return;
//Right recursion
fun(root.right);
//Intermediate processing accumulation link
sum = sum + root.val;
root.val = sum;
//Left recursion
fun(root.left);
}
}
summary
So that's the end of the binary tree. Shit, recursion is too difficult. Shit.