Better reading experience: http://www.abmcar.top/archives/codeforceshello2022
Complete source code: https://github.com/abmcar/ACM/tree/master/OpenjudgeNow/Codeforces/Hello%202022
Tip from the front row: the questions in this field are very disgusting and are not recommended

A. Stable Arrangement of Rooks

Main idea of the topic: give you a board of size n * n so that you can put k pieces. There are no other pieces in the same row of any piece, and it is also satisfied to move it up, down, left and right. Judge whether there is a scheme. If it exists, output it; otherwise, output - 1
Idea: it's easy to think of Queen n, but it has nothing to do with queen n. We can easily construct it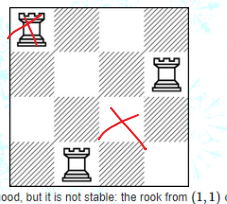In this case, it is not difficult to prove that this method puts the most pieces one by one along the diagonal distribution. In this way, an n*n board can put (n+1)/2 pieces. We only need to simply judge + output
code:

void work()
{
    cin >> n >> k;
    if ((n + 1) / 2 < k)
    {
        cout << -1 << endl;
        return;
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            if (i == j && i % 2 == 1 && ((i+1)/2 <= k))
                cout << "R";
            else
                cout << ".";
        }
        cout << endl;
    }
}

B. Integers Shop

(this is a very disgusting classified discussion)
Give you n intervals for you to choose, and each interval has its price. If you choose a number l,r, the number between l-r can be given to you for free. Ask the first 1, 2, 3,..., n intervals for the minimum cost of selecting the largest number
Idea: at first, when you see this problem, you can confidently write a record and replace the left and right endpoint positions and the greedy cost. We know that it needs the maximum selection length, so we should choose the cheapest on the left and the cheapest on the right, but at this time, we don't consider a large range to cover all cases
So you wrote an additional judgment. If a large interval is desirable, abandon the left and right endpoint interval, take a large interval, and hand it in wa2
Let's consider such a situation
Red and blue are the previous minimum left and right end points, purple is a cheaper large range, and the dark blue below is the new area
When we discard red and blue for purple and then judge the dark blue range, we need to take dark blue and purple, but in fact, dark blue and blue are the best, so we can't abandon the left and right endpoint ranges
We need to record the left and right end intervals and record the large interval at the same time. If the large interval is all and better, we can choose the large interval
code:

void work()
{
    cin >> n;
    ll lCost, rCost;
    lCost = rCost = 1e12;
    ll cntLen = 0;
    ll lenCost = 1e12;
    cntL = 1e12;
    cntR = 0;
    for (int i = 1; i <= n; i++)
    {
        cin >> l[i] >> r[i] >> c[i];
        // cout << cntL << " " << cntR << endl;
        // cout << l[i] << " " << r[i] << endl;
        if (cntL > l[i])
        {
            cntL = l[i];
            lCost = c[i];
        }
        if (cntR < r[i])
        {
            cntR = r[i];
            rCost = c[i];
        }
        if (cntL == l[i])
            lCost = min(lCost, c[i]);
        if (cntR == r[i])
            rCost = min(rCost, c[i]);
        cntC = lCost + rCost;
        if (r[i] - l[i] + 1 > cntLen)
            cntLen = r[i] - l[i] + 1,lenCost = c[i];
        if (cntLen == r[i] - l[i] + 1)
            lenCost = min(lenCost,c[i]);
        
        // cout << cntL << " " << cntR << " " << cntLen << endl;
        if (cntLen == cntR - cntL + 1)
            cntC = min(lenCost, cntC);

        cout << cntC << endl;
    }
}

C. Hidden Permutations

I'll give you an array p and an array q. I don't know the content of p. the initial value of q is qi = i, that is, 1,2,3,4... n. you can ask for the value of qi, but after each query
Q[i] will be replaced by Q[Pi]
You need to ask again 2n times to give you the original array p
Idea: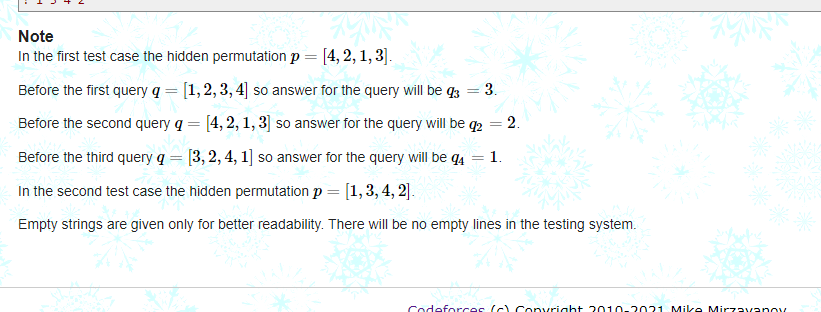
Observing the example, it is not difficult to find the change of Q[1]: 1-4-3-1. Since q is initially known, we find that p[1] = 4,p[4] = 3,p[3] = 1. It is not difficult to prove that P[Q[X]] = Q[Q[X]]. We count whether it has been selected in the way of joint query. If we solve each one in this way, we can find p in 2n times. (because the worst case is to find one in two queries, and it can not be all the worst)
code:

int find(int x)
{
    if (x == father[x])
        return x;
    father[x] = find(father[x]);
    return father[x];
}

int query(int pos)
{
    cout << "? " << pos << endl;
    int targetVal;
    cin >> targetVal;
    return targetVal;
}

void work()
{
    cin >> n;
    M.clear();
    cnt = 0;
    for (int i = 1; i <= n; i++)
        father[i] = i;
    for (int k = 1; k <= n; k++)
    {
        if (cnt == n)
            break;
        if (M[find(k)] != 0)
            continue;
        int nowNum = query(k);
        while (M[nowNum] == 0)
        {
            int newNum = query(k);
            M[nowNum] = newNum;
            father[find(nowNum)] = find(newNum);
            nowNum = newNum;
            cnt++;
            if (cnt == n)
                break;
        }
    }
    // ll tot = 0;
    // for (int i = 1; i <= n; i++)
    //     tot += M[i];
    cout << "! ";
    for (int i = 1; i <= n; i++)
        cout << M[i] << " ";
    cout << endl;
}