Game link
Dashboard - Codeforces Round #731 (Div. 3) - Codeforces
A. Shortest Path with Obstacle
meaning of the title
Give the two-dimensional coordinates of three points A, B and F, and ask you the minimum distance between points A and B without passing through F.
thinking
First, calculate the example between two points AB to judge whether F is in the middle. If it is + 2, it will not move if it is not.
As soon as there are more variables, I feel a little dizzy. I won't come back until a few minutes later
code
#include<stack>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<deque>
#include<vector>
#include<iostream>
#include<map>
#include<set>
#include<iomanip>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define ll long long
using namespace std;
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
const int inf=0x3f3f3f3f;
int T,a1,a2,b1,b2,f1,f2,d;
signed main()
{
#ifndef ONLINE_JUDGE
freopen("IO\\in.txt","r",stdin);
freopen("IO\\out.txt","w",stdout);
#endif
IOS
cin>>T;
while (T--)
{
cin>>a1>>a2>>b1>>b2>>f1>>f2;
d=abs(a1-b1)+abs(a2-b2);
//cout<<d<<" "<<f2<<" "<<min(a2,b2)<<" "<<max(a2,b2)<<endl;
if (a1==b1&&f1==a1&&(f2<=max(a2,b2)&&f2>=min(a2,b2))) d+=2;
if (a2==b2&&f2==a2&&(f1<=max(a1,b1)&&f1>=min(a1,b1))) d+=2;
cout<<d<<endl;
}
return 0;
}B.Alphabetical Strings
meaning of the title
Give a string to judge whether it is legal or not. There is always an increment on both sides starting from a
thinking
First determine the position of a, and then go to the double pointers on both sides to find the next one. If not, it is illegal. Finally, if all lengths are legal, it is legal.
code
#include<stack>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<deque>
#include<vector>
#include<iostream>
#include<map>
#include<set>
#include<iomanip>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define ll long long
using namespace std;
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
const int inf=0x3f3f3f3f;
string st;
int T,len,pos,l,r;
signed main()
{
#ifndef ONLINE_JUDGE
freopen("IO\\in.txt","r",stdin);
freopen("IO\\out.txt","w",stdout);
#endif
IOS
cin>>T;
while (T--)
{
cin>>st;
len=st.length();
pos=-1;
for (int i=0;i<len;i++)
if (st[i]=='a') {pos=i;break;}
//Find the location of a
l=pos,r=pos;
//Double pointer
bool boo=true;
if (len==1&&st[0]!='a'||pos==-1) boo=false;
for (int i=2;i<=len;i++)
{
if (l>0&&st[l-1]==char(i+'a'-1)) {l--;continue;}
if (r<len-1&&st[r+1]==char(i+'a'-1)) {r++;continue;}
//Neither pointer is found. continue indicates that it is not found
boo=false;
break;
}
if (boo) cout<<"YES\n";
else cout<<"NO\n";
}
return 0;
}C. Pair Programming
meaning of the title
The two sequences are merged without disturbing their respective sequences, so that all numbers not equal to 0 in the sequence are currently less than or equal to k. k has an initial value. If 0, k+1
thinking
It is also a greedy double pointer. If you encounter 0, you will add it. Anyway, it will not have any impact. The more k, the better; If you encounter something that is not 0, judge whether the current k can be satisfied, and if so, point to the next one; If not, then the sequence cannot be satisfied
code
#include<stack>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<deque>
#include<vector>
#include<iostream>
#include<map>
#include<set>
#include<iomanip>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define ll long long
using namespace std;
const int N = 500;
int a[N],b[N],t1,t2,k,n,m,cnt,ans[N],T;
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
const int inf=0x3f3f3f3f;
signed main()
{
#ifndef ONLINE_JUDGE
freopen("IO\\in.txt","r",stdin);
freopen("IO\\out.txt","w",stdout);
#endif
IOS
cin>>T;
while (T--)
{
cin>>k>>n>>m;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=m;i++) cin>>b[i];
t1=1;t2=1;cnt=0;
bool boo=true;
while (1)
{
if (cnt==n+m) break;
if (a[t1]==0&&t1<=n)
{
ans[++cnt]=a[t1++];
k++;
continue;
}
if (b[t2]==0&&t2<=m)
{
ans[++cnt]=b[t2++];
k++;
continue;
}
//0
if (a[t1]<=k&&t1<=n)
{
ans[++cnt]=a[t1++];
continue;
}
if (b[t2]<=k&&t2<=m)
{
ans[++cnt]=b[t2++];
continue;
}
//Not 0
boo=false;
break;
//There is no continue, indicating that there is no way to make it continue
}
if (!boo) cout<<-1;
else for (int i=1;i<=cnt;i++) cout<<ans[i]<<" ";
cout<<endl;
}
return 0;
}D. Co-growing Sequence
meaning of the title
Give a sequence and ask how much you want to add at present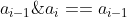
thinking
We can go first or get a tmp=a[i-1] | a[i]; This is the number we need to reach, and then use XOR to get the difference between a[i], output a[i]^tmp, and then assign this tmp to a[i], which can be used next time i+1
code
#include<stack>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<deque>
#include<vector>
#include<iostream>
#include<map>
#include<set>
#include<iomanip>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define ll long long
using namespace std;
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
const int inf=0x3f3f3f3f;
const int N = 2e5+7;
ll t[40],b,a[N],x;
int T,n,tmp;
signed main()
{
#ifndef ONLINE_JUDGE
freopen("IO\\in.txt","r",stdin);
freopen("IO\\out.txt","w",stdout);
#endif
IOS
b=1;
for (int i=1;i<=31;i++)
{
b<<=1;
t[i]=b-1;
}
cin>>T;
while (T--)
{
cin>>n;
for (int i=1;i<=n;i++)
cin>>a[i];
cout<<0<<" ";
for (int i=2;i<=n;i++)
{
tmp=(a[i]|a[i-1]);
cout<<(tmp^a[i])<<" ";
a[i]=tmp;
}
cout<<endl;
}
return 0;
}E. Air Conditioners
meaning of the title
There are air conditioners at k positions, and the temperature is t. every other position, the temperature + 1, find the minimum temperature at each place in this interval
thinking
I don't know how to deal with a place when I do it, because there are many things affecting this place, including those from the left and those from the right. I don't know until I make up the question. We only need to sweep it twice, one on the left and one on the right.
First assign an inf to each place, and then copy the air conditioning temperature of each place to the array. Scanning on the left is to deal with the impact of all air conditioners on the right, so it doesn't matter what I said before. The same is true when sweeping back on the right. Look at the code
code
#include<stack>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<deque>
#include<vector>
#include<iostream>
#include<map>
#include<set>
#include<iomanip>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define ll long long
using namespace std;
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
const int inf=0x3f3f3f3f;
const int N = 3e5+7;
ll a[N],n,k,T,pos[N];
signed main()
{
#ifndef ONLINE_JUDGE
freopen("IO\\in.txt","r",stdin);
freopen("IO\\out.txt","w",stdout);
#endif
IOS
cin>>T;
while (T--)
{
cin>>n>>k;
memset(a,0x3f/2,sizeof(a));
for (int i=1;i<=k;i++) cin>>pos[i];
for (int i=1;i<=k;i++) cin>>a[ pos[i] ];
for (int i=2;i<=n;i++) a[i]=min(a[i],a[i-1]+1);
for (int i=n-1;i>=1;i--) a[i]=min(a[i],a[i+1]+1);
for (int i=1;i<=n;i++) cout<<a[i]<<" ";
cout<<endl;
}
return 0;
}F. Array Stabilization (GCD version)
meaning of the title
Given a sequence, each operation makes a[i] and a[i+1] take gcd, and then give a[i]. When it goes beyond the boundary, that is, when i=n, a[n] and a[1] take gcd. After asking how many times, the whole sequence is equal
thinking
Let's think about the violence algorithm first, and then optimize it.
First enumerate the number of times, starting from 1-n, then enumerate each interval, and then query the gcd. The time complexity is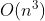
GCD: ST table for optimizing enumeration interval length
Optimize enumeration interval length (Times): two point answer
ST table used to be used to go to min or max, but you just need to change it to gcd. I've learned. The binary answer is because it is monotonous, "illegal", "illegal" "Illegal", "legal" "Legal"
But my code I don't know what's wrong. Ask the great God for an answer
code
#include<stack>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<cstring>
#include<deque>
#include<vector>
#include<iostream>
#include<map>
#include<set>
#include<iomanip>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define ll long long
using namespace std;
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
const int inf=0x3f3f3f3f;
const int N = 4e5+7;
int lg2[N],f[N][30],n,T,l,r,mid;
inline int query(int l,int r)
{
int w=lg2[r-l+1];
//cout<<"!"<<l<<" "<<r<<" "<<f[l][w]<<" "<<f[r-(1<<w)+1][w]<<endl;
return GCD(f[l][w],f[r-(1<<w)+1][w]);
}
inline void ST()
{
for (int i=n;i>=1;i--)
for (int j=1;i+(1<<j)-1<=n;j++)
f[i][j]=GCD(f[i][j-1],f[i+(1<<j-1)][j-1]);
}
inline void init()
{
for (int i=2;i<=n;i++)
lg2[i]=lg2[i>>1]+1;
}
inline bool check(int k)
{
int tmp=-1;
if (k==0) return true;
for (int i=1;i<=n;i++)
{
int t=query(i,i+k-1);
//cout<<t<<endl;
if (tmp==-1) tmp=t;
else if (tmp!=t) return false;
}
return true;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("IO\\in.txt","r",stdin);
freopen("IO\\out.txt","w",stdout);
#endif
IOS
cin>>T;
init();
while (T--)
{
cin>>n;
for (int i=1;i<=n;i++) cin>>f[i][0];
for (int i=n+1;i<=2*n;i++) f[i][0]=f[i-n][0];
n<<=1;
ST();
n>>=1;
//cout<<"T="<<T<<endl;
int l=0,r=n,mid;
while(l<r){
//out<<l<<" "<<r<<endl;
mid=(l+r)/2;
if(check(mid)){
r=mid;
}
else{
l=mid+1;
}
}
if(r)r--;
cout<<r<<endl;
}
return 0;
}
/*
INPUT
1
5
5 13 2 10 11
OUTPUT
4
ANSWER
2
*/
G. How Many Paths?
To be supplemented
Links
Codeforces Round #731 (Div. 3) +382_ Blog of the sunspot - CSDN blog
summary
ST(Sparse Table) table, Chinese name sparse table, is a data structure.
ST table is often used to solve the problem of repeatable contribution.
What is a repeatable contribution problem?
For example: if you want to find the maximum number of 10 numbers, you can find the GCD of the first 6 numbers first. Although several numbers in the middle are calculated repeatedly, it does not affect the final answer.
Common repeatable contribution problems include interval maximum, interval bitwise sum, interval bitwise OR, interval GCD, etc. Problems such as interval sum are not repeatable contribution problems.