Content:
Receive a string of message characters from the keyboard and output the corresponding Huffman code. At the same time, it can translate the code string generated by Huffman code and output the corresponding message string.
Design requirements:
(1). Construct a Huffman tree;
(2). Implement Huffman coding and decode the code string generated by Huffman coding;
(3). The characters and weights in the program are variable to realize the flexibility of the program.
Steps:
algorithm analysis
This design uses structure array to store Huffman tree.
Two functions are designed in the program:
The function HuffmanTree() is used to construct a Huffman tree;
The function HuffmanCode() is used to generate Huffman code and output it.
In telegraph communication, messages are transmitted in binary code. When sending, it is necessary to convert the characters in the message into binary code string, that is, encoding; When accepting, it is necessary to convert the received binary code string into the corresponding character sequence, that is, decoding. Because the frequency of characters in the character set is non-uniform, the total length of the message should be as short as possible when transmitting the message. Therefore, if a character set is designed for unequal length coding, it is required that the coding of any character is not the prefix of other character codes. This coding is called prefix coding. The code obtained from Huffman tree is the optimal prefix code, also known as Huffman code. The character set and the probability distribution of each character are given, and the Huffman tree is constructed. The left branch of each branch node in the Huffman tree is marked as 0 and the right branch is marked as 1. Connecting the labels on the path from the root to each leaf is the code of the character represented by the leaf.
In the program, the main function inputs some characters and character weights according to the prompt, and the program outputs Huffman code; If a message is input, Huffman decoding can be output.
1. Algorithm of constructing Huffman tree
Input different characters in the main program, count the times of different characters as the weight of the character, and store it in the data [] array. Assuming that there are n characters, there are n leaf nodes, and the constructed Huffman tree has 2n-1 nodes. The specific steps are as follows:
Store n characters (leaf nodes) and their weights in the first n array elements of HuffNode array, and set the parents and left and right children of 2n-1 nodes to - 1
Among all nodes, select the nodes m1 and M2 with the minimum and sub small weights, and indicate the positions of the two nodes in the array with x1 and x2. Merge the two trees with roots HuffNode[x1] and HuffNode[x2] to become the left and right children of the new node HuffNode[n+i], with the weight of m1+m2
Repeat the above process and merge n-1 times to construct a Huffman tree. The generated n-1 nodes are placed in n~2n-2 cells of the array HuffNode [].
2.Huffman coding and decoding algorithm
Starting from the leaf node huffnode [i] (0 < = I < n) of Huffman tree, through HuffNode[c] Parents find their parents. Through lchild and rchild fields, we can know whether HuffNode[c] is a left branch or a right branch. If it is a left branch, bit[n-1-i]=0; Otherwise, bit[n-1-i]=1
Taking HuffNode[c] as the starting point, repeat the above process until the root of the tree is found, that is, Huffman coding is carried out.
When decoding, first input the binary code string, put it in the array code, and end the input with carriage return.
Compare the code with the code table. If it is 0, turn to the left subtree; If it is 1, turn to the right subtree until the leaf node ends. The data field of the output leaf node, that is, the corresponding character.
Outline design:
| HuffmanTree() | Construct a Huffman tree |
| HuffmanCode() | Generate huffman encoding and output |
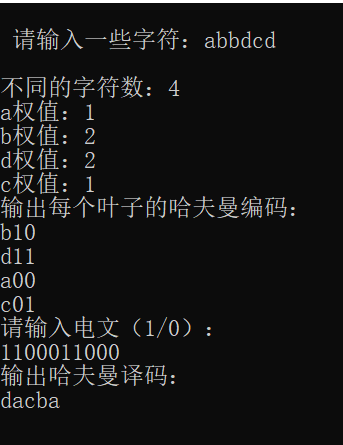
Operation results:
Source code:
#include<stdio.h>
#include<conio.h>
#define MAXVALUE 10000
#define MAXLEAF 30
#define MAXNODE MAXLEAF*2-1
#define MAXBIT 50
#define NULL 0
typedef struct node {
char letter;
int weight;
int parent;
int lchild;
int rchild;
} HNodeType;
typedef struct {
char letter;
int bit[MAXBIT];
int start;
} HCodeType;
typedef struct {
char s;
int num;
} Message;
//Construction algorithm of Huffman tree
void HuffmanTree(HNodeType HuffNode[],int n,Message a[]) {
int i,j,m1,m2,x1,x2,temp1;
char temp2;
for(i=0; i<2*n-1; i++) { //HuffNode [] initialization
HuffNode[i].letter=NULL;
HuffNode[i].weight=0;
HuffNode[i].parent=-1;
HuffNode[i].lchild=-1;
HuffNode[i].rchild=-1;
}
for(i=0; i<n-1; i++)
for(j=i+1; j<n-1; j++)
if(a[j].num>a[i].num) {
temp1=a[i].num;
a[i].num=a[j].num;
a[j].num=temp1;
temp2=a[i].s;
a[i].s=a[j].s;
a[j].s=temp2;
}
for(i=0; i<n; i++) {
HuffNode[i].weight=a[i].num;
HuffNode[i].letter=a[i].s;
}
for(i=0; i<n-1; i++) { //Constructing Huffman tree
m1=m2=MAXVALUE;
x1=x2=0;
for(j=0; j<n+i; j++) { //Find the two subtrees with the smallest weight
if(HuffNode[j].parent==-1&&HuffNode[j].weight<m1) {
m2=m1;
x2=x1;
m1=HuffNode[j].weight;
x1=j;
} else if(HuffNode[j].parent==-1&&HuffNode[j].weight<m2) {
m2=HuffNode[j].weight;
x2=j;
}
}
//Merge the two subtrees found into one subtree
HuffNode[x1].parent=n+i;
HuffNode[x2].parent=n+i;
HuffNode[n+i].weight=HuffNode[x1].weight+HuffNode[x2].weight;
HuffNode[n+i].lchild=x1;
HuffNode[n+i].rchild=x2;
}
}
//Generate Huffman code
void HuffmanCode(int n,Message a[]) {
HNodeType HuffNode[MAXNODE];
HCodeType HuffCode[MAXLEAF],cd;
int i,j,c,p;
char code[30],*m;
HuffmanTree(HuffNode,n,a);//Building Huffman tree
for(i=0; i<n; i++) { //Find the Huffman code of each leaf node
cd.start=n-1;
c=i;
p=HuffNode[c].parent;
while(p!=-1) { //From leaf node up to tree root
if(HuffNode[p].lchild==c)
cd.bit[cd.start]=0;
else
cd.bit[cd.start]=1;
cd.start--;
c=p;
p=HuffNode[c].parent;
}
for(j=cd.start+1; j<n; j++) //The Huffman code of each leaf node and the start bit of the code are saved
HuffCode[i].bit[j]=cd.bit[j] ;
HuffCode[i].start=cd.start;
}
printf("Output Huffman code of each leaf:\n");
for(i=0; i<n; i++) { //Output Huffman code of each leaf node
HuffCode[i].letter=HuffNode[i].letter;
printf("%c",HuffCode[i].letter);
for(j=HuffCode[i].start+1; j<n; j++)
printf("%d",HuffCode[i].bit[j]);
printf("\n");
}
printf("Please enter the message (1)/0): \n");
for(i=0; i<30; i++)code[i]=NULL;
scanf("%s",&code);
m=code;
c=2*n-2;
printf("Output Huffman decoding:\n");
while(*m!=NULL) {
if(*m=='0') {
c=i=HuffNode[c].lchild;
if(HuffNode[c].lchild==-1&&HuffNode[c].rchild==-1) {
printf("%c",HuffNode[i].letter);
c=2*n-2;
}
}
if(*m=='1') {
c=i=HuffNode[c].rchild;
if(HuffNode[c].lchild==-1&&HuffNode[c].rchild==-1) {
printf("%c",HuffNode[i].letter);
c=2*n-2;
}
}
m++;
}
printf("\n");
}
int main() {
Message data[30];
char s[100],*p;
int i,count=0;
printf("\n Please enter some characters:");
scanf("%s",&s);
for(i=0; i<30; i++) {
data[i].s=NULL;
data[i].num=0;
}
p=s;
while(*p) {
for(i=0; i<=count+1; i++) {
if(data[i].s==NULL) {
data[i].s=*p;
data[i].num++;
count++;
break;
} else if(data[i].s==*p) {
data[i].num++;
break;
}
}
p++;
}
printf("\n");
printf("Different number of characters:%d\n",count);
for(i=0; i<count; i++) {
printf("%c",data[i].s);
printf("Weight:%d",data[i].num);
printf("\n");
}
HuffmanCode(count,data);
getch();
}