1. Summary
In the first chapter of the collection series, we learned that the implementation classes of Map are HashMap, LinkedHashMap, TreeMap, IdentityHashMap, WeakHashMap, Hashtable, Properties, and so on.
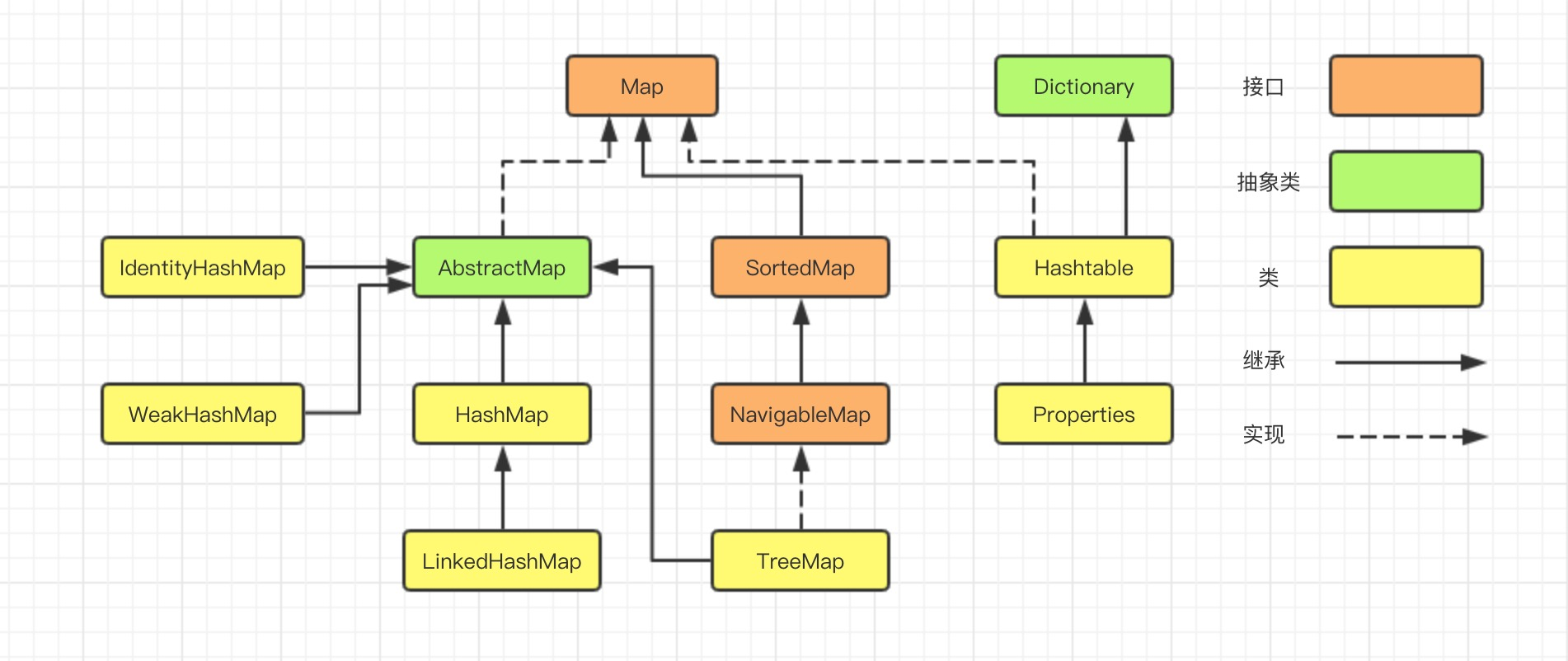
HashMap has always been a hot topic, and I promise you'll need it if you go out for an interview!
This article mainly combines the differences between JDK1.7 and JDK1.8 to discuss the data structure and implementation function of HashMap in depth. Let's not talk too much about it. Go straight to the topic!
2. Introduction
In programming, HashMap is a very frequently used container class that allows key values to be placed in null elements.Except for methods that do not synchronize, the rest are roughly the same as Hashtable, but unlike TreeMap, the container does not guarantee the order of elements. The container may re-hash elements as needed, and the order of elements may be re-scattered, so the order of iterating over the same HashMap at different times may be different.
The HashMap container is essentially a hash array structure, but there is the possibility of hash conflicts when elements are inserted;
In the case of Hash conflict, there are two implementations of conflict, one is open address (when a hash conflict occurs, continue to look for hash values that do not conflict) and the other is zipper (where conflicting elements are put in the list).Java HashMap uses the second method, zipper.
In jdk1.7, HashMap is mainly composed of an array + a list of chains. When a hash conflict occurs, the conflicting elements are put into the list.
Starting with jdk1.8, HashMap is mainly implemented by Array + Chain List + Red-Black Tree, which is one more implementation than jdk1.7.When the chain length exceeds 8, it becomes a red-black tree, as shown in the figure.
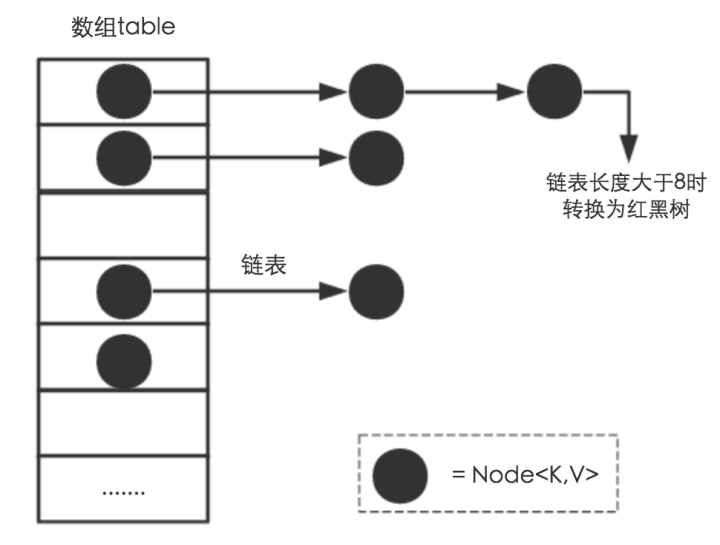
About the implementation of red and black trees, because it is too long, the design of red and black trees is also introduced in the Collection Series article, which is not detailed here.
3. Source Code Analysis
Opening the source analysis of HashMap directly shows that there are five key parameters:
- threshold: Indicates the limit of key-value pairs that a container can hold.
- loadFactor: Load factor.
- modCount: Records the number of modifications.
- size: Represents the actual number of key-value pairs.
- table: An array of hash buckets in which key-value pairs are stored.
public class HashMap<K,V> extends AbstractMap<K,V>
implements Map<K,V>, Cloneable, Serializable {
//Limits of key-value pairs that can be accommodated
int threshold;
//Load factor
final float loadFactor;
//Record number of modifications
int modCount;
//Actual number of key-value pairs
int size;
//Hash bucket array
transient Node<K,V>[] table;
}Next, look at the class Node, an internal class of HashMap that implements the Map.Entry interface, essentially a mapping (key-value pair)
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;//hash value
final K key;//k-key
V value;//Value value
Node<K,V> next;//Next element in the list
}In the data structure of HashMap, there are two parameters that can affect the performance of HashMap: initial capacity and load factor.
Initial capacity is the initial length of the table (default is 16);
load factor refers to the threshold value for automatic expansion (default value is 0.75);
Threshold is the number of Nodes (key-value pairs) for the maximum amount of data that HashMap can hold. The formula threshold = capacity * Load factor is calculated.When the number of entries exceeds capacity*load_factor, the container automatically expands and re-hashes, double the capacity of the expanded HashMap, so the length of the array is always the n-th power of 2.
The initial capacity and load factor can also be modified by specifying parameters when the object is initialized, such as:
Map map = new HashMap(int initialCapacity, float loadFactor);
However, the default load factor of 0.75 is a balanced choice between space and time efficiency, and we recommend that you do not modify it unless you have a lot of memory space and a high requirement for time efficiency under special circumstances of time and space, you can reduce the value of the load factor Load factor; conversely, you can increase the negative value if memory space is tight and time efficiency is not high.The value of the load factor loadFactor, which can be greater than 1.At the same time, for scenarios with more elements inserted, you can set the initial capacity to be larger and reduce the number of re-hashes.
There are many implementations of HashMap's internal functions. This paper will make a step-by-step analysis from the following points.
- Gets the array subscript through K;
- Detailed execution of put method;
- resize expansion process;
- get method gets parameter value;
- remove deletes elements;
3.1. Obtain array subscripts through K
Whether you add, delete, or find key-value pairs, positioning the array is a critical first step. Opening any of the add, delete, and find methods of hashMap shows from the source code that getting array subscripts by key mainly takes three steps, where length refers to the size of the container array.
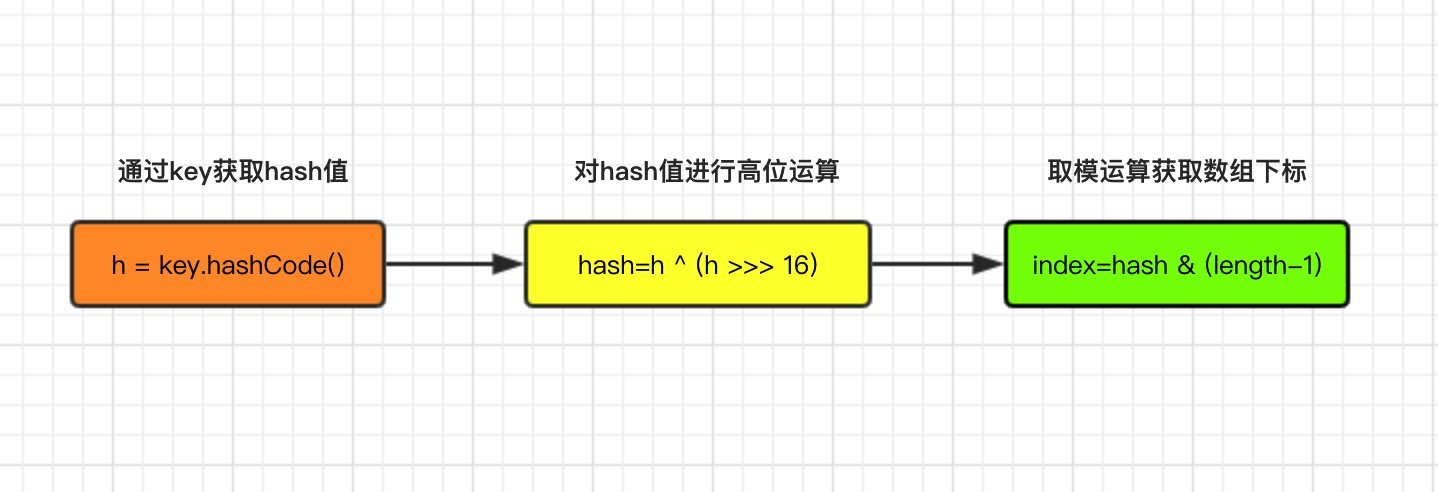
Source Part:
/**Get hash value method*/
static final int hash(Object key) {
int h;
// h = key.hashCode() takes the hashCode value for the first step (jdk1.7)
// H ^ (h >>>> 16) is the second high-bit participation operation (jdk1.7)
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);//jdk1.8
}
/**Get Array Subscript Method*/
static int indexFor(int h, int length) {
//Source for jdk1.7, jdk1.8 does not have this method, but the implementation works the same way
return h & (length-1); //Step 3 Modular Operation
}3.2. Detailed execution of put method
The put(K key, V value) method adds the specified key, value pair to the map.The method first looks for the map to see if it contains the K, returns it directly if it already contains it, and inserts the element into the container if it is not found.The insertion process is as follows:
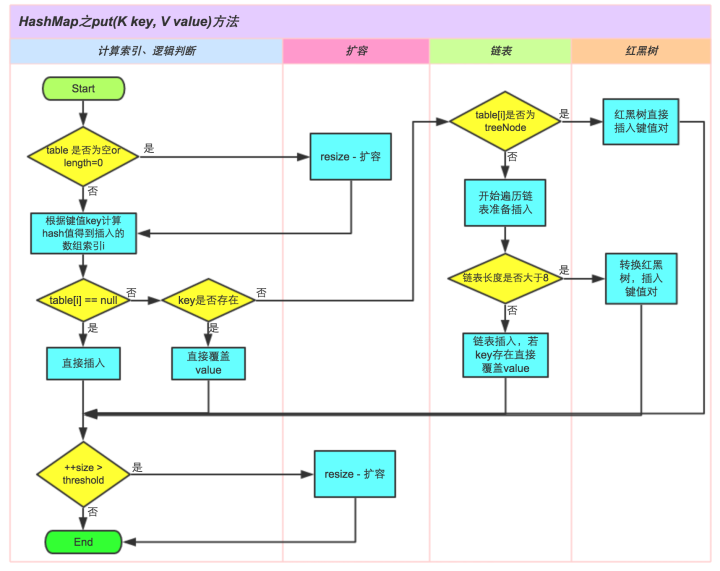
Specific implementation steps
- 1. Determine if the key value is empty or null for the array table[i], otherwise resize() is performed to expand;
- 2. Calculate the array index I that hash is worth inserting based on the key value. If table[i]==null, add a new node directly.
- 3. When table[i] is not empty, determine whether the first element of table[i] is the same as the key passed in, if the same directly overrides value;
- 4. Determine whether table[i] is treeNode, that is, whether table[i] is a red-black tree or if it is a red-black tree, insert key-value pairs directly into the tree;
- 5. Traverse the table[i], to determine if the length of the chain table is greater than 8, if it is greater than 8, convert the chain table to a red-black tree, and perform the insertion operation in the red-black tree, otherwise insert the chain table; in the traversal process, if the key already exists, it can directly overwrite the value;
- 6. After successful insertion, determine whether the actual key value exceeds the maximum threshold for the number size, and if it exceeds, expand the capacity;
put Method Source Part
/**
* put Method
*/
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}Insert Element Method
/**
* Insert Element Method
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//1. Determine if the array table is empty or null
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//2. Judgement array subscript table[i]==null
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
//3. Determine if the first element of table[i] is the same as the key passed in
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
//4. Determine whether table[i] is treeNode
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
//5. Traverse the table[i] to determine if the chain length is greater than 8
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
//Length greater than 8, transition to red-black tree structure
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
//The incoming K element already exists, overwriting value directly
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
//6. Determine if size exceeds maximum capacity
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}Among them, there is a difference from jdk1.7, step 4 added the red-black tree insertion method, source part:
/**
* Insertion of red and black trees
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
//dir: Traversal direction, hash value of ph:p node
int dir, ph; K pk;
//Red-black trees are size based on hash values
// -1:Left Child Direction 1:Right Child Direction
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
//Return directly to the current node if the key exists
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
//If the Key of the type currently inserted and the node being compared is Comparable, then compare directly through this interface
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
//Try to find the target element in the left or right subtree of p
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
//Get the direction of traversal
dir = tieBreakOrder(k, pk);
}
//All of the above if-else judgments are directed toward the next traversal, which is dir
TreeNode<K,V> xp = p;
//When the following if judgment is entered, the target action element, xp, is found
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
//Insert a new element
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
//Since TreeNode may degenerate into a linked list in the future, the next attribute of the linked list needs to be maintained here
xp.next = x;
//Complete node insertion
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
//Some adjustments will be made after the insertion is completed
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}3.3. resize Expansion Process
Before we talk about the dynamic expansion of HashMap for jdk1.8, let's take a look at the implementation of HashMap for jdk1.7, because the implementation of JDK1.8 code is more than twice as complex as Java 1.7, mainly because Java 1.8 introduced the redtree design, but the implementation ideas are very different!
Expansion Implementation of 3.3.1 and jdk1.7
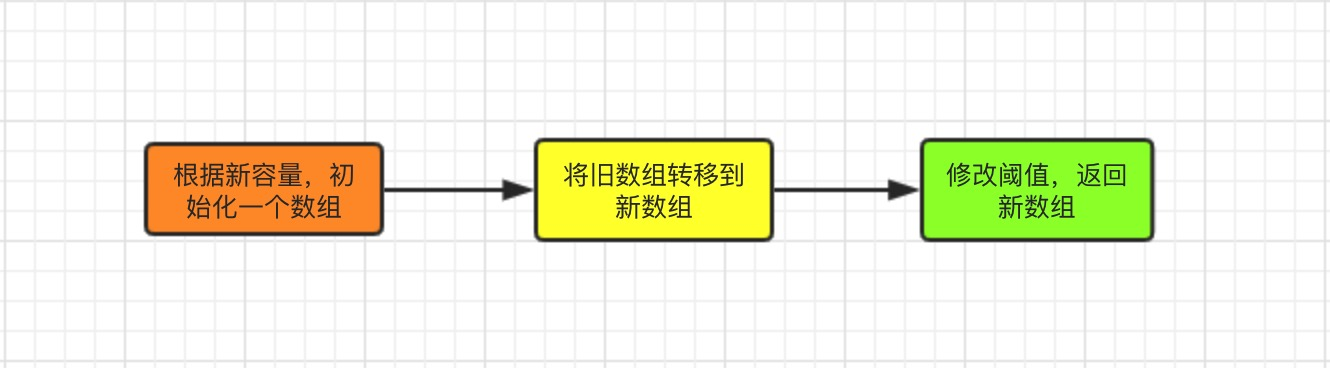
Source Part
/**
* JDK1.7 Expansion Method
* Incoming new capacity
*/
void resize(int newCapacity) {
//Reference to Entry array before expansion
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
//If the size of the array before expansion has reached its maximum (2^30)
if (oldCapacity == MAXIMUM_CAPACITY) {
//Modify the threshold to the maximum value of int (2^31-1) so that it will not expand in the future
threshold = Integer.MAX_VALUE;
return;
}
//Initialize a new Entry array
Entry[] newTable = new Entry[newCapacity];
//Transfer data to a new Entry array, which contains the most important repositioning
transfer(newTable);
//HashMap's table property references a new Entry array
table = newTable;
threshold = (int) (newCapacity * loadFactor);//Modify Threshold
}transfer Copy Array Method, Source Part:
//Traverse through each element, rehash at a new capacity, and place on a new array
void transfer(Entry[] newTable) {
//src references an old Entry array
Entry[] src = table;
int newCapacity = newTable.length;
for (int j = 0; j < src.length; j++) {
//Traversing through an old Entry array
Entry<K, V> e = src[j];
//Get each element of the old Entry array
if (e != null) {
//Release object references from old Entry arrays (after a for loop, the old Entry arrays no longer reference any objects)
src[j] = null;
do {
Entry<K, V> next = e.next;
//Recalculate the position of each element in the array
//Implementing logic is the same modulo operation as above
int i = indexFor(e.hash, newCapacity);
//Tag Array
e.next = newTable[i];
//Place elements on an array
newTable[i] = e;
//Access the elements on the next Entry chain and iterate through them
e = next;
} while (e != null);
}
}
}jdk1.7 Extension Summary: References to newTable[i] are assigned to e.next, that is, the head insertion of single-chain lists is used, where new elements are always placed at the head of the chain; elements placed first on an index are eventually placed at the end of the Entry chain if a hash conflict occurs, which is different from Jdk1.8.Elements on the same Entry chain in the old array may be placed in different positions in the new array by recalculating the index position.
Expansion implementation of 3.3.2 and jdk1.8
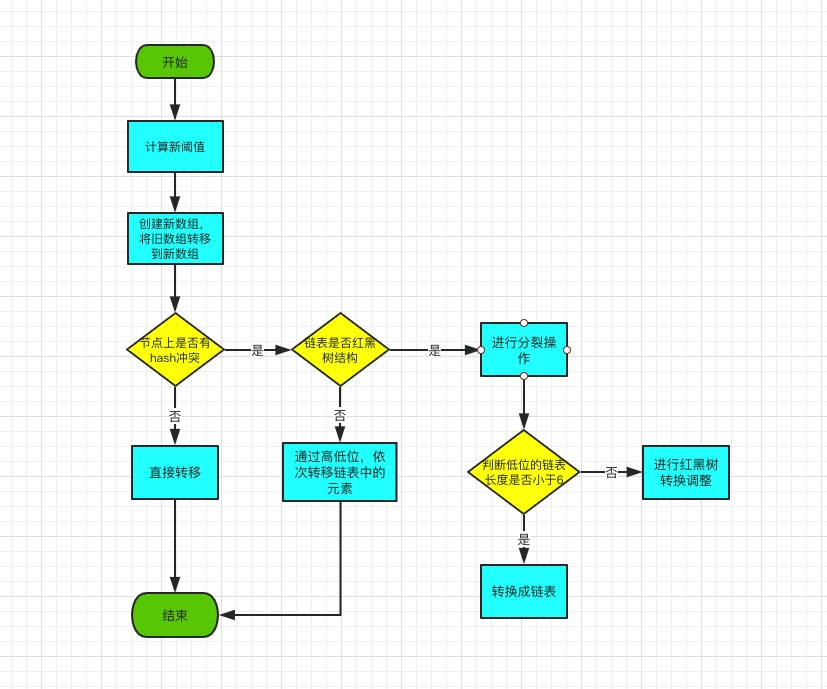
The source code is as follows
final Node<K,V>[] resize() {
//Reference to node array before expansion
Node<K,V>[] oldTab = table;
//Old capacity
int oldCap = (oldTab == null) ? 0 : oldTab.length;
//Old threshold
int oldThr = threshold;
//New capacity, threshold initialization is 0
int newCap, newThr = 0;
if (oldCap > 0) {
//If the old capacity has exceeded the maximum capacity, let the threshold equal the maximum capacity, and do not expand in the future
threshold = Integer.MAX_VALUE;
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// Without exceeding the maximum, expand to twice the original
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
//If the old capacity is not doubled beyond the maximum value and the old capacity is not less than the initialization capacity of 16, the doubling will occur
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
//Initialization capacity set to threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
//0 is initialized with default values
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
//Calculate a new threshold value, if the new capacity or threshold is greater than or equal to the maximum capacity, then use the maximum value directly as the threshold value and no longer expand
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
//Set a new threshold
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
//Create a new array and reference
table = newTab;
//If the old array has data, that is, expansion rather than initialization, execute the following code, otherwise initialization will end here
if (oldTab != null) {
//Poll Old Array for All Data
for (int j = 0; j < oldCap; ++j) {
//Reference the current node with a new node, then release the reference of the original node
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
//If E has no next node, proving that there is no hash conflict on this node, direct the reference to e to the new array location
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
//!!!Split if it is a red-black tree
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else {
// Chain list optimization heavy hash block
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
//Start polling from the first element in the list. If the current element adds a bit of 0, it will be placed on the current list. If it is 1, it will be placed at the "j+oldcap" position to generate the "low" and "high" lists.
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
//Elements are constantly added to the tail, not in reverse order as in 1.7
loTail.next = e;
//New elements are always tail elements
loTail = e;
}
else {
//A high-order list, like a low-order list, continually adds elements to the end of the list
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
//The low-bit list is placed at the location of the j index
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
//Place the high-bit list at the location of the index (j+oldCap)
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}The logic of 1.7 and 1.8 is similar, but the main difference is in the method of tree node splitting ((TreeNode<K, V>)e).split().
/**
* Red-Black Tree Splitting Method
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
//The current reference to this node, the root node of the tree on this index
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
//The number of initial tree nodes at both high and low positions is set to 0
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
//bit=oldcap, where you can tell if the new bit is 0 or 1, if 0 it is on the low tree, if 1 it is on the high tree, where is a two-way chain table first
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
//!!!If the low-bit list length is less than the threshold of 6, turn the tree into a list and place it in the j-index position of the new array
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
//High not empty, red-black tree conversion
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab);
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}untreeify method that converts a tree into a one-way chain table
/**
* Convert a tree into a one-way chain table
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}The treeify method, which converts a list of chains to a red-black tree, performs color conversion, left-handed, right-handed, etc. based on the characteristics of the red-black tree
/**
* The chain list is converted to a red-black tree, which is color converted, left-handed, right-handed, etc. according to the characteristics of the red-black tree
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
//Make left-handed and right-handed adjustments
root = balanceInsertion(root, x);
break;
}
}
}
}
moveRootToFront(tab, root);
}jdk1.8 will recalculate hash value after re-expanding, because n is doubled. Assuming initial tableSize = 4 expands to 8, it means 0100 to 1000 change (one to the left is twice). In expanding, only one bit of original hash value and one bit to the left (the value of newtable) will be used to judge whether the original hash value and the operation are 0 or 1, then the index of 0 will not change, and the voice of 1 will not change.Quote to original index + oldCap;
Its implementation is shown in the following flowchart:
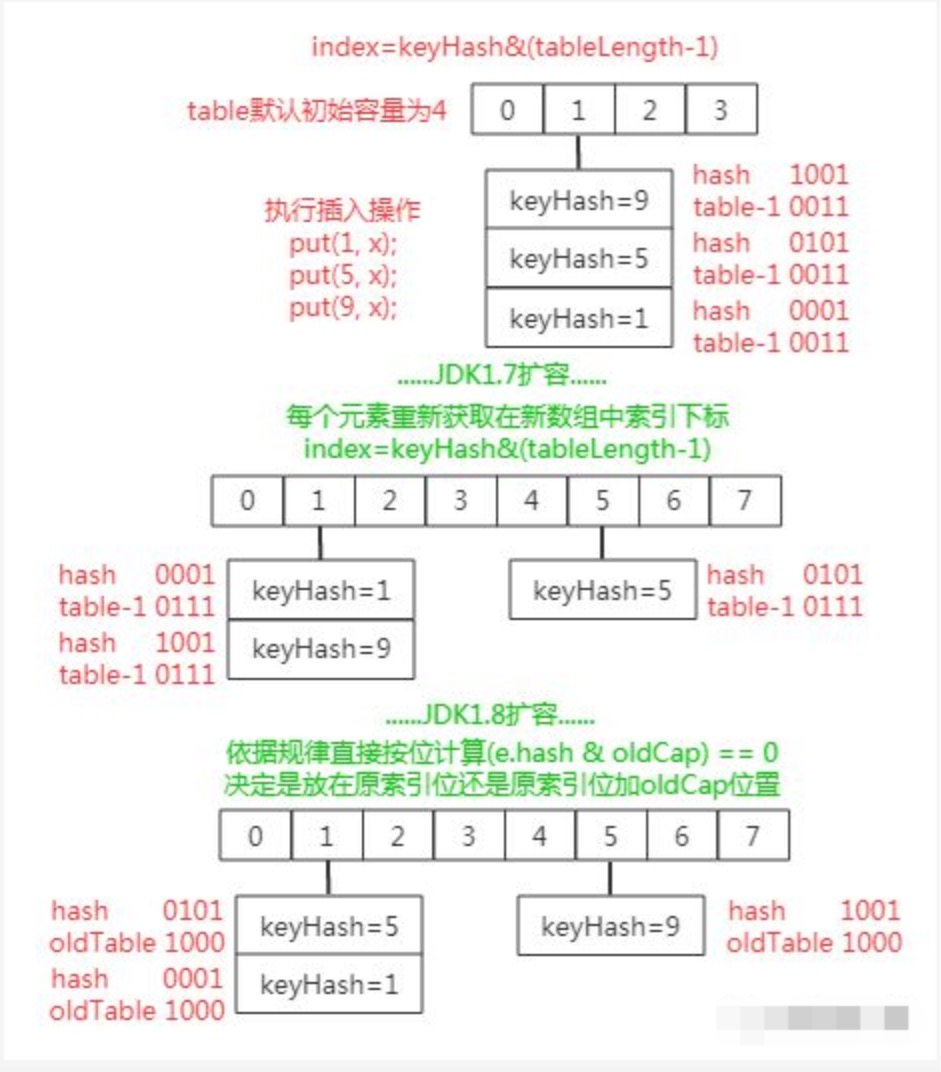
You can see that because hash values are random, hash bitwise is random with 0 (index position before expansion) and 1 (index position before expansion plus array length before expansion) obtained by newTable above, so the expansion process can randomly distribute elements of previous hash conflicts to different indexes, which is one of JDK1.8 Optimization points.
In addition, when rehash is in JDK1.7, when the old list migrates the new list, the list elements are inverted if the array index positions of the new table are the same, but as can be seen from the above figure, JDK1.8 is not inverted.
At the same time, since the hash conflict in JDK1.7 only uses a chain table structure to store conflict elements, scaling up is only to recalculate their storage locations.In JDK1.8, the chain table structure is converted to a red-black number structure to store conflicting elements in order to achieve a certain degree of hash conflict at the same index. Therefore, when the current index is expanded, if the element structure is a red-black tree and the number of elements is less than the chain table restore threshold, the tree structure will be reduced or restored directly to the chain table structure (its implementation is spli in the code snippet above).T() method).
3.4. get method to get parameter value
The get(Object key) method returns the corresponding value based on the specified key value, getNode (hash (key), key) gets the corresponding Node object e, and then returns e.value.So getNode() is the core of the algorithm.
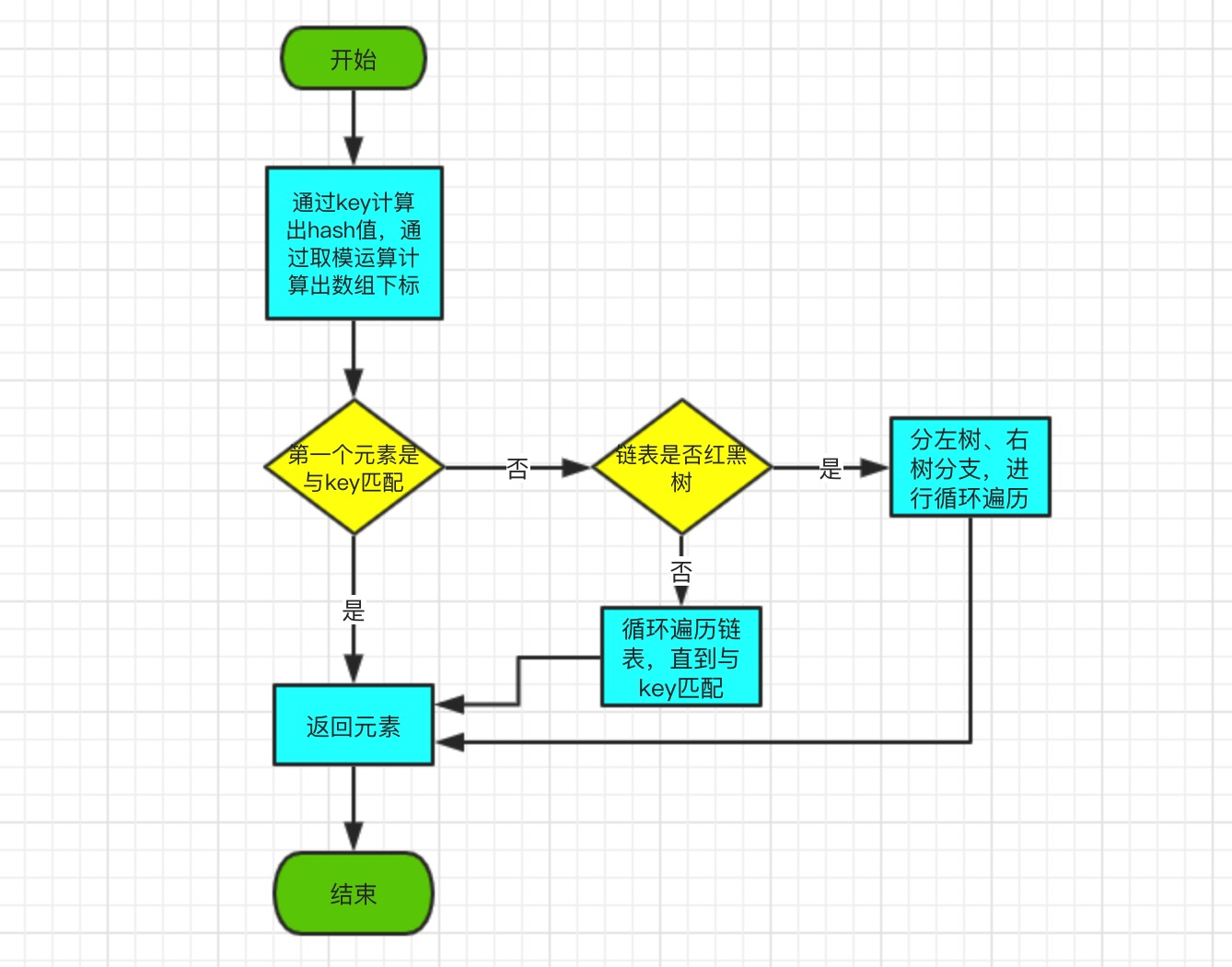
get method source part:
/**
* JDK1.8 get Method
* Getting parameter values by key
*/
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}Node Node method obtained by hash value and key, source part:
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
//1. Determine if the first element matches the key
if (first.hash == hash &&
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
//2. Determine whether the chain table is red-black tree structure
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
//3. Direct circular judgment if it is not a red-black tree structure
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}TreeNode for the specified k is found in the red-black tree, source part:
/**
* There are many different scenarios, mainly because the hash is the same but the key value is different. The core of the lookup still falls on the key value.
*/
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
//Determines whether the hash of the element to query is on the left side of the tree
if ((ph = p.hash) > h)
p = pl;
//Determines whether the hash of the element to query is on the right side of the tree
else if (ph < h)
p = pr;
//Query element hash is the same as current tree node hash
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
//All three steps above are normal ways to find objects in a binary search tree
//If hash is equal, but the content is not equal
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
//If you can compare against compareTo, compare against compareTo
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
//Continue querying on the right child based on compareTo results
else if ((q = pr.find(h, k, kc)) != null)
return q;
//Continue querying on the left child based on compareTo results
else
p = pl;
} while (p != null);
return null;
}Get method, first get the corresponding array subscript through hash() function, and then judge in turn.
- 1. Determine if the first element matches the key, and return the parameter value if it matches.
- 2. Determine whether the chain table is a red-black tree or not, if it is a red-black tree, enter the red-black tree method to get the parameter values;
- 3. If it is not a red-black tree structure, loop directly until the parameters are obtained.
3.5, remove delete element
The purpose of remove(Object key) is to delete the Node corresponding to the key value. The logic of this method is implemented in removeNode(hash(key), key, null, false, true).
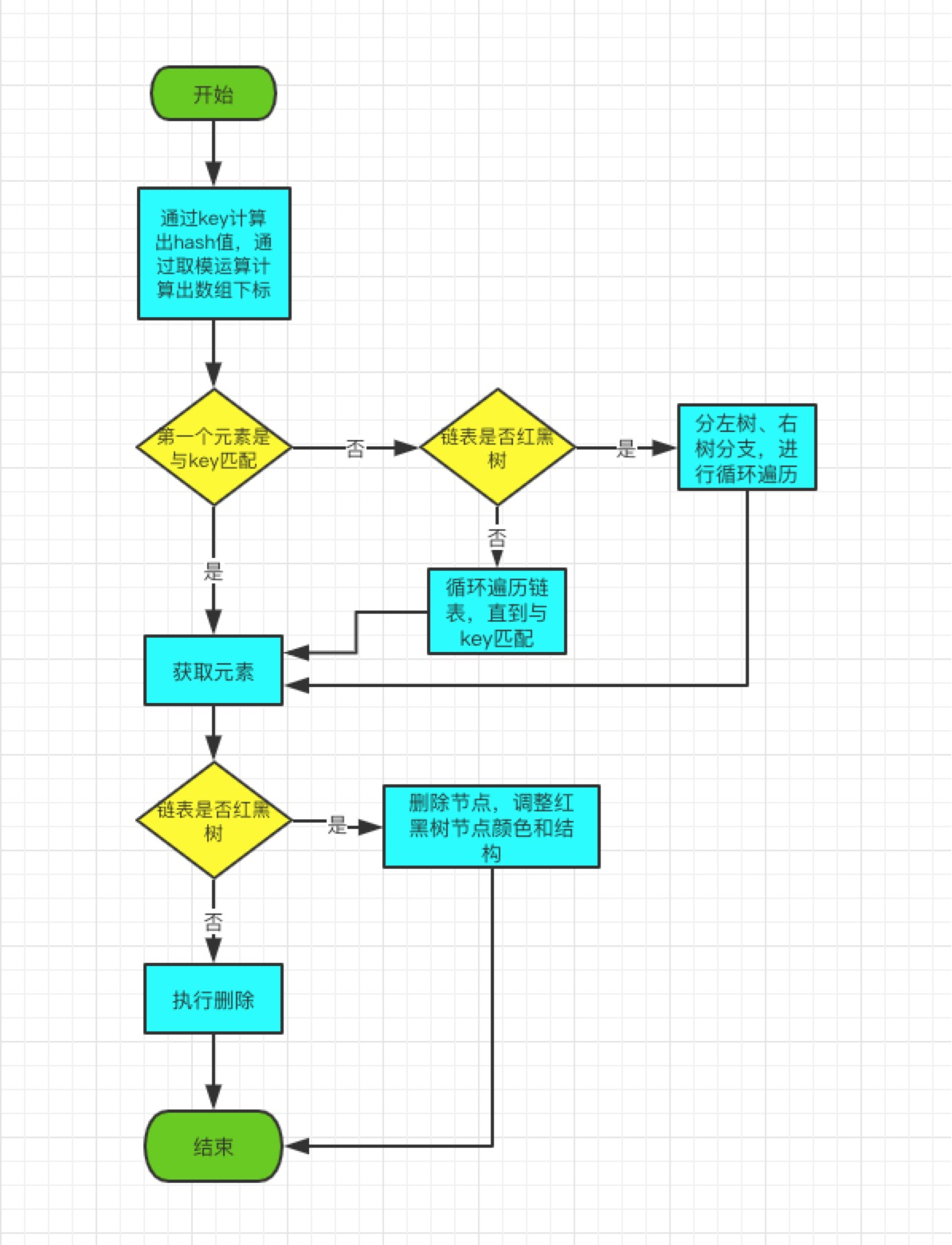
remove method, source part:
/**
* JDK1.8 remove Method
* Remove objects by key
*/
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}Remove Node Node Method via key, Source Part:
/**
* Remove Node Node by key
*/
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
//1. Determine if the element to be deleted exists
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
//2. Determine if the first element is what we're looking for
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
//3. Determine whether the current conflict chain table has a red-black tree structure
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
//4. Loop finds elements in the list that need to be deleted
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
//The logic above is basically to find the node to delete the element
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
//5. If the current conflict chain table structure is a red-black tree, execute the red-black tree deletion method
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)
tab[index] = node.next;
else
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}removeTreeNode Remove Red-Black Tree Node Method, Source Part:
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null)
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
if (first == null)
return;
if (root.parent != null)
root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // too small
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
if (replacement != p) {
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
//Determine if red-black tree structure adjustment is required
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { // detach
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}The deletion logic implementation of jdk1.8 is more complex, and there are more red-black tree nodes to delete and adjust than jdk1.7:
- 1. Default judgment on whether the first element of the chain list is to be deleted;
- 2. If the first one is not, continue to determine if the current conflict chain list is a red-black tree, and if so, go into the red-black tree to find it.
- 3. If the current conflict chain table is not a red-black tree, it will be judged directly in the chain table until it is found.
- 4. Delete the nodes found. If it is a red-black tree structure, color conversion, left-hand and right-hand adjustments will be made until the red-black tree characteristics are satisfied.
4. Summary
1. If the key is an object, remember to override the equals and hashCode methods within the object entity class, otherwise the parameter values cannot be obtained by the object key when querying!
2. Compared with JDK1.7, JDK1.8 introduces the red-black tree design. When the chain length is longer than 8, the chain table will be converted into the red-black tree structure. If the chain table in conflict is long, the implementation of red-black tree greatly optimizes the performance of HashMap, making the query efficiency twice as fast as JDK1.7!
3. In the case of large arrays, you can initialize a capacity for the Map ahead of time, avoiding frequent expansion when inserting, because expansion itself consumes performance!
5. Reference
1. JDK1.7&JDK1.8 Source
2,Meituan Technical Team - Recognition of HashMap in the Java 8 Series
3,Short Book - JDK1.8 Red and Black Tree Implementation Analysis - This fish is waterproof
4,Short Book - HashMap Expansion in JJDK 1.8
5,Java HashMap Basic Interview FAQ
Author: Fried Chicken Coke
Source: www.pzblog.cn