Collision detection is generally used in game design, such as the now more popular game "King Glory". We can see in the game that heroes generally go to the attack area of the local defense tower and will be attacked. But when programmers are downloading the code, they can not see it. They can only use a piece of code to express it. This is to use collision detection, and also to determine whether two objects intersect.
Here I will mainly talk about three main intersecting judgments, the other collisions are evolved under these conditions:
First, write the class code of rectangle, circle and straight line.

//Rectangle class
class rect{
private:
 double xl;
 double yl;
 double xr;
 double yr;
public:
 rect(double _xl, double _yl, double _xr, double _yr)
  :xl(_xl), yl(_yl), xr(_xr), yr(_yr)
 {}
 bool collideRL(linear& l);
 bool collideRC(Circle& c);
 bool collideRR(rect& r, rect& r1);
};
//Circle class
class Circle{
private:
 double x;
 double y;
 double r;
public:
 Circle(double _x, double _y, double _r)
  :x(_x), y(_y), r(_r)
 {}
 double getCx(){ return x; }
 double getCy(){ return y; }
 double getCr(){ return r; }
};
//Straight line class
class linear{
private:
 double k;
 double b;
 double x1;
 double x2;
public:
 linear(double _k, double _b, double _x1, double _x2)
  :k(_k), b(_b), x1(_x1), x2(_x2)
 {}
 double getlk(){ return k; }
 double getlb(){ return b; }
 double getlx1(){ return x1; }
 double getlx2(){ return x2; }
};

1. Collision Detection of Lines and Rectangles
   The main method I use here is to judge whether the diagonal line of a rectangle and the intersection point of a straight line are in the rectangle. The figure is as follows:

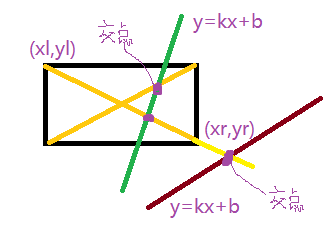
As shown in the figure above, we only need to determine whether the intersection point of the straight line and the rectangular diagonal intersects in the rectangle. The function code is as follows:

bool rect::collideRL(linear& l)
{
//Four constants are defined to represent the slope of two diagonals of a rectangle and the intersection point with the y axis.
 double k1, k2;
 double b1, b2;
 k1 = (yl - yr) / (xl - xr);
 b1 = yl - xl*k1;
 k2 = -k1;
 b2 = yl - xr*k2;
 double k = l.getlk();
 double b = l.getlb();
 double x1 = l.getlx1();
 double x2 = l.getlx1();
 double x, y;
 //Calculate the desired X and Y values of the intersection point of a straight line and a rectangular diagonal.
 x = (b - b1) / (k1 - k);
 y = (b - b1) / (k1 - k)*k + b;
 //Judging whether the intersection point is in the rectangle
 if ((xl < x && x < xr)|| (xr < x && x < xl))
 {
  if ((y>yl&&y<yr) || (y>yr&&y < yl))
  {
   cout << "A straight line intersects a rectangle." << endl;
   return true;
  }
 }
 x = (b - b2) / (k2 - k);
 y = (b - b2) / (k2 - k)*k + b;
 if ((xl < x && x < xr) || (xr < x && x < xl))
 {
  if ((y>yl&&y<yr) || (y>yr&&y < yl))
  {
   cout << "A straight line intersects a rectangle." << endl;
   return true;
  }
 }
 cout << "The line is separated from the rectangle" << endl;
 return false;
}

1. Collision Detection of Circle and Rectangle
   The first method is:
   In judging the intersection of a circle and a rectangle, I mainly divide it into the following situations: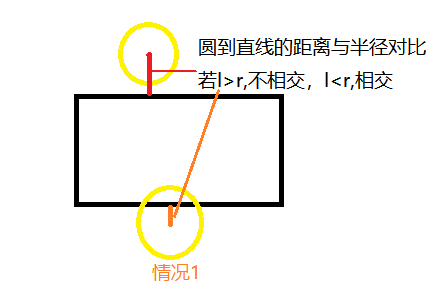
   
   
   
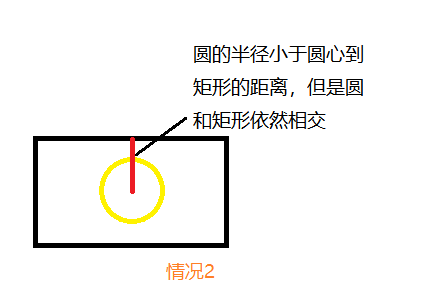
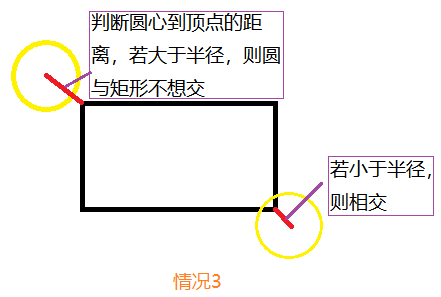
   The function code is expressed as:

bool rect::collideRC(Circle& c)
{
double x = c.getCx();
 double y = c.getCy();
 double r = c.getCr();
 double s = sqrt(pow(x - xl, 2) + pow(y - yl, 2));
 double s1 = sqrt(pow(x - xl, 2) + pow(y - yr, 2));
 double s2 = sqrt(pow(x - xr, 2) + pow(y - yr, 2));
 double s3 = sqrt(pow(x - xr, 2) + pow(y - yl, 2));
 if ((r > xl&&r < xr) || (r<xl&&r>xr))
 {
  if ((r<yl&&r>yr) || (r>yl&&r < yr))
  {
   cout << "A circle intersects a rectangle." << endl;
   return true;
  }
 }
 if ((fabs(y - yl) < r) || (fabs(y - yr) < r) || (fabs(x - xl) < r) || (fabs(x - xr) < r))
 {
  if ((r > xl&&r < xr) || (r<xl&&r>xr) || (r<yl&&r>yr) || (r>yl&&r < yr))
  {
   cout << "A circle intersects a rectangle." << endl;
   return true;
  }
 }
 if (s > r&&s1 > r&&s2 > r&&s3 > r)
 {
  cout << "The circle is separated from the rectangle" << endl;
  return false;
 }
 cout << "A circle intersects a rectangle." << endl;
 return true;
 }

(2) The second method:
To be simpler than the second method in the first method, but the logic is somewhat circumscribed, use the following figure to simply express the following: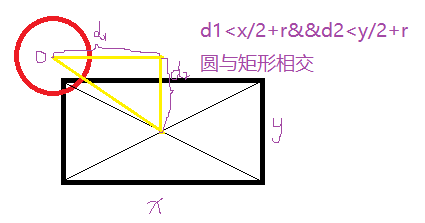

The function code is expressed as:

bool rect::collideRC(Circle& c)
{
 double x = c.getCx();
 double y = c.getCy();
 double r = c.getCr();
 if (fabs((r.xl + r.xr) / 2 - x) < (fabs(r.xl - r.xr) / 2 + r)
 {
  if (fabs((r.yl + r.yr) / 2 - y) < (fabs(r.yl - r.yr)/ 2 + r)
  {
   cout << "A circle intersects a rectangle." << endl;
   return true;
  }
 }
 cout << "The circle is separated from the rectangle" << endl;
 return false;
}

1. Collision Detection of Rectangles and Rectangles
   The second method used for collision detection of rectangle and rectangle is similar to that used for collision detection of circle and rectangle. ** The following figures are shown as follows: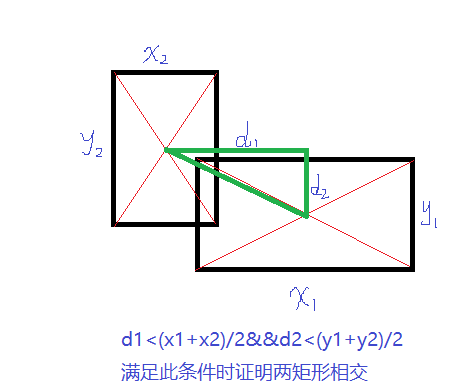
   
   Represented in code as follows:

bool rect::collideRR(rect& r,rect& r1)
{
 //Judgment principle: the projection of two rectangular midpoints connected on the x-axis is less than half of the sum of the edges parallel to the x-axis; the y-axis is the same;
 if (fabs((r.xl + r.xr) / 2 - (r1.xl + r1.xr) / 2) < (fabs(r.xl - r.xr) + fabs(r1.xl - r1.xr)) / 2)
 {
  if (fabs((r.yl + r.yr) / 2 - (r1.yl + r1.yr) / 2) < (fabs(r.yl - r.yr) + fabs(r1.yl - r1.yr)) / 2)
  {
   cout << "Two rectangles intersect" << endl;
   return true;
  }
 }
 cout << "Separation of two rectangles" << endl;
 return false;
}

The above is the understanding of collision detection, one of the problems is that this method can not be used to judge whether two objects are tangent, only to prove that they are separated and intersected, because the type of definition is double, and can not be used to directly judge equal; so the above method can only judge whether or not to collide, not when to meet.