Groups and numbers are as follows according to the parameter data range:

Contains n groups of data, each group of data input two numbers a and b;

The first case: the data range of a and b is relatively small

Range: 1 ≤ n ≤ 100001 ≤ n ≤ 10000,1 ≤ b ≤ a ≤ 2000;

In this simplest case, use the formula directly: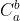  = 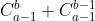Preprocessing, and then directly access the subscript of the answer;

#include<iostream>

using namespace std;

const int N = 2010;
int c[N][N];
const int mod = 1e9 + 7;

int main()
{
    for(int i = 0;i <= 2000;i ++)
    for(int j = 0;j <= i;j ++)
    if(!j)c[i][j]=1;
    else c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
    int n;
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
    return 0;
}

The second case: the data range of a and b is relatively large

Range: 1 ≤ n ≤ 100001 ≤ n ≤ 10000,1 ≤ b ≤ a ≤ 1e5;

Practice: in this case, use the formula: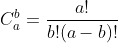It is also to preprocess first and finally subscript the answer, in which Fermat's small theorem is used to find the inverse element;

Proof of Fermat's small theorem:

First, the definition of Fermat's small theorem: if a and p are coprime, then there is；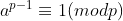

The code is as follows:

#include<iostream>

using namespace std;

const int N = 100010;
int fact[N],infact[N];
int mod = 1e9 + 7;

int qmi(int a,int p,int mod)
{
    int sum = 1;
    while(p)
    {
        if(p&1)sum = (long long)sum * a%mod;
        p = p >> 1;
        a = (long long)a*a%mod;
    }
    return sum%mod;
}
int main()
{
    fact[0] = 1;infact[0]=1;
    for(int i = 1;i < N;i ++)
    {
        fact[i] = (long long)fact[i-1]*i % mod;
        infact[i] = (long long)infact[i-1]*qmi(i,mod-2,mod)%mod;
    }
    int n;
    cin >> n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<(long long)fact[a]*infact[b]%mod*infact[a-b]%mod<<endl;
    }
}

Supplement some formulas of congruence equation:

1. If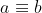(mod p)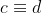，(mod p)，

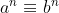Then a+cB + D (mod p) (except addition, subtraction and multiplication, all have the same formula, except Division),(mod p)；

2. If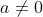, p cannot divide a, i.e. gcd(a,p)=1, then there is b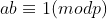

Prove that:

Lemma: if a and p are coprime, then there is x, y is an integer so that ax+by=1;

First proof lemma:

Consider that all {ax + by | x, y belong to integer}

Assume a minimum integer n;

So exist；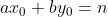

Where n must be divided by a;

Otherwise, a = n*q + r < 0 < R < n;

r = 

The third case: there are very few test samples, but the values of a and b are very large;

Range: 1 < = n < = 20; 1<=b<=a<=1e18; 1<=p<=1e5;

Practice: use Lucas theorem

Lucas theorem: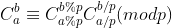

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;


int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b, int p)
{
    if (b > a) return 0;

    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2, p) % p;
    }
    return res;
}


int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}


int main()
{
    int n;
    cin >> n;

    while (n -- )
    {
        LL a, b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }

    return 0;
}

The fourth case: without mod, the result may be very large

Practice: high precision is required

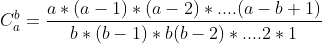
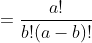
Decomposition quality factor =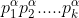

First, preprocess all the quality factors and find out the number of times of quality factors;

Example:

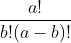
For example, the number of times p is required. First find out how many numerators and denominators there are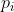How do I subtract the denominator from the p in the numerator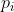, the difference is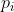Number of;

So a! How many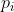And?

We can get it this way:

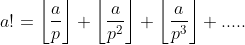
Take out all p first, take out all p squares, then take out the third power of p, and so on, all p will be taken out;

So the first step came: sun out all the primes within one to five thousand;

Step 2: find the number of times of each prime number;

Step 3: multiply all quality factors with high-precision multiplication;

The code is as follows:

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;


const int N = 5010;

int primes[N], cnt;
int sum[N];
bool st[N];


void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}


int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }

    vector<int> res;
    res.push_back(1);

    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);

    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

Author: yxc
 Link: https://www.acwing.com/activity/content/code/content/53401/
Source: AcWing
 The copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.