Collection common interfaces and classes
Collection in java is very important. It is both a container and a reference data type. There are many interfaces and classes related to collection. Regardless of concurrent, the most common are as follows:
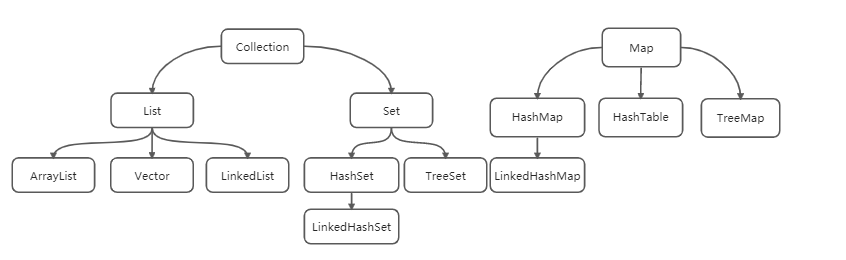
As can be seen from the above figure, it is mainly divided into two camps, one is Collection, the other is Map, and the Collection is divided into List and Set.
List is ordered. This order actually refers to the order in which elements are put and taken out, not the size of elements.
Set is out of order, which means that the order in which elements are put and taken out cannot be guaranteed. However, it can be seen from the above that HashSet and TreeSet are listed under set. In fact, because the underlying storage of TreeSet is a tree structure, this storage must be compared in size. Therefore, although the storage and retrieval of elements in TreeSet are disordered, the sizes of elements themselves are sequential.
In addition, HashSet has a subclass LinkedHashSet. A linked list is added to the original storage structure to record the storage order, so it can be said to be orderly.
Map is a Key value pair. HashMap is similar to HashSet, and TreeMap is similar to TreeSet, but they are all aimed at keys. In fact, the bottom layer of HashSet is HashMap, and the bottom layer of TreeSet is TreeMap.
In addition to the above, there are two things that are not commonly used in work, but may often appear in interviews. One is vector and the other is HashTable. The reason why we often ask questions in interviews is mainly because vector is compared with ArrayList. Vector is thread safe because the methods are decorated with synchronized. HashTable is often compared with HashMap, because HashTable is thread safe and its methods are decorated with synchronized.
In addition, many of their implementations are similar, even in jdk1 It was basically the same before 8. In addition, judging from the comments of the JDK source code, both HashTable and Vector are jdk1 0, while ArrayList and HashMap are 1.2.
Although Vector and HashTable are thread safe, they are not commonly used. When thread safe collections are needed, jdk1.0 is a better choice 5. Related classes in the added concurrent package, such as ConcurrentHashMap, CopyOnWriteArrayList and CopyOnWriteArraySet.
In addition to the above overview, there are many important technical points in these specific collection classes, such as:
ArrayList capacity expansion principle
The bottom layer of ArrayList is array, which is defined as Object [], in jdk1 In the source code of 8, there is also a default length of 10, a default empty array and a record array. The length variable size is used. The relevant definitions are as follows:
transient Object[] elementData;
private static final int DEFAULT_CAPACITY = 10;
private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
private int size;
When "new ArrayList < > ()" is used to create an ArrayList object, the default empty array will be assigned to elementData first. When the add method is called, it will judge whether elementData is the same as the default empty array object. If it is different, the array will be expanded.
public ArrayList() {
this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA;
}
public boolean add(E e) {
ensureCapacityInternal(size + 1); // Increments modCount!!
elementData[size++] = e;
return true;
}
private void ensureCapacityInternal(int minCapacity) {
if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
ensureExplicitCapacity(minCapacity);
}
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// overflow-conscious code
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
private void grow(int minCapacity) {
// overflow-conscious code
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1);
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
elementData = Arrays.copyOf(elementData, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
if (minCapacity < 0) // overflow
throw new OutOfMemoryError();
return (minCapacity > MAX_ARRAY_SIZE) ?
Integer.MAX_VALUE :
MAX_ARRAY_SIZE;
}
As can be seen from the above source code, when adding data to the ArrayList for the first time, the actual length of the array after capacity expansion is 10.5
When the array length exceeds 10, the new array length is "oldcapacity + (oldcapacity > > 1)". The important part here is the section "oldcapacity > > 1". In the bit operation, moving right represents dividing by 2, and moving left represents multiplying by 2. It is obvious that the expansion is 1.5 times of the original array.
At that time, it should be noted that there is judgment behind, that is, when the value of 1.5 times exceeds MAX_ARRAY_SIZE, the maximum value is integer MAX_ VALUE.
LinkedList structure and feature analysis
The array structure at the bottom of ArrayList determines that its random access speed is very fast, but if you want to insert and delete, you need to move all the elements behind the position, which will be inefficient. Therefore, for the operation of inserting and deleting more, you need to use LinkedList to improve efficiency.
The underlying layer of the LinkedList is a linked list structure. The so-called linked list actually means that each node not only stores the data itself, but also records the information of adjacent nodes. Only through adjacent nodes can another node be found. Logically, the nodes are connected like a chain.
In jdk1 8 in the source code, LinkedList has several important attributes, as follows:
transient int size = 0; transient Node<E> first; transient Node<E> last;
These three attributes are actually the use length of the List, the first Node and the tail Node, and the Node node is an internal class of LinkedList, which is defined as follows:
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
You can see that this Node not only records the data itself, but also records the information of the previous Node and the next Node. This structure can actually be called a two-way linked list. There is also a one-way linked list, that is, only record the next Node without recording the information of the previous Node.
There is also a special linked list called circular linked list, that is, the next node of the last node will point to the first node, forming a ring.
Of course, the linked list in the LinkedList here is not a circular linked list. This can be seen from the source code of adding elements to it:
public boolean add(E e) {
linkLast(e);
return true;
}
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
It can be seen that the so-called tail interpolation method is adopted here, that is, the new element will be placed behind the last node, the previous node of the new node will be set as the last node before, and then the next node of the previous last node will be set as a new node.
As mentioned earlier, the underlying structure in ArrayList is array. Therefore, when randomly accessing elements, that is, using subscripts to remove elements, you can actually directly remove elements in the array with array subscripts. However, the linked list structure in LinkedList cannot be taken in this way. You can only traverse until you find the element you need to find.
Obviously, if the search is traversed from front to back, if it happens to be the first node, it only needs to cycle once, but if it happens to be the last one, it needs to traverse the length of the set.
Therefore, an optimization is carried out when randomly accessing elements in the LinkedList. The binary search algorithm is used, that is, the set element is divided into two. When the index of the accessed element is located in the first half of the set, it will traverse from front to back. If the index of the accessed element is located in the second half of the set, it will traverse from back to front. The relevant source code is as follows:
public E get(int index) {
checkElementIndex(index);
return node(index).item;
}
Node<E> node(int index) {
// assert isElementIndex(index);
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
HashSet
The bottom layer of a HashSet is actually a HashMap. When a HashSet object is created, the bottom layer will actually create a HashMap object. This key is the data to be put into the HashSet, and Value is a fixed object. Putting data into the HashSet is actually putting data into the underlying HashMap, which can be seen from the source code:
public HashSet() {
map = new HashMap<>();
}
public boolean add(E e) {
return map.put(e, PRESENT)==null;
}
In view of the characteristics of HashSet, some principled contents actually need to be combined with HashMap.
LinkedHashSet
The underlying layer of the LinkedHashSet is LinkedHashMap, so the principle content also needs to be combined with LinkedHashMap.
TreeSet
The bottom layer of TreeSet is TreeMap.
Combined with the source code to see HashMap
The data in the Map is stored in the form of key value pairs in jdk1 In 8, the bottom layer of HashMap uses the structure of array + linked list + red black tree to store data.
First, the so-called key value pairs in HashMap are in jdk1 8 is actually an internal class of Node, which inherits from another internal class Entry (this was directly used before JDK1.8). It is roughly defined as follows:
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
...
}
When you save data to the HashMap, you actually generate the Node object and store it in the Node array.
In the process of saving, an array length is involved first. It can be seen from the source code that the underlying array will not be created when creating HashMap, but the variables of loading factor are assigned, for example:
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
The underlying array is actually created when putting data. The source code of the put method is as follows:
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
This method looks complex, and it also involves most of the key knowledge points in HashMap.
First, judge the table variable of the underlying array here. If it is null, a table variable will be created.
Secondly, when creating an array, it is not only the first time to create it. Since it is an array, the length is fixed. When it is full, it is necessary to expand the array, and the expansion of the array means to generate a new array.
Of course, the HashMap does not wait until it is full.
The length of this array needs to be specified whether it is created for the first time or expanded. The calculation of this length involves many technical points.
In the HashMap usage specification, it is actually recommended to specify an initial length, so that the latter does not need to be calculated. Especially when determining the collection size, specifying the length during creation can reduce the expansion operation.
When creating the underlying array, there are two important properties, one is the default length, the other is the default loading factor. The default length is defined in the source code as follows:
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
As mentioned earlier, shifting one bit to the right means multiplying by 2, so shifting four bits to the right actually means multiplying by 2 four times, that is, 12222 = 16, so the default length is 16
The default load factor is defined in the source code as follows:
static final float DEFAULT_LOAD_FACTOR = 0.75f;
This loading factor is used to judge the capacity expansion of the underlying array. For example, it is 0.75 here, which means that when the actual amount of data exceeds 0.75 times the capacity of the array, the capacity of the underlying array will be expanded to twice the original capacity.
When creating the initial array and expanding the capacity of the array, one detail is that the length of the array will eventually be the n-power of 2. Even if the n-power of 2 is specified when creating the HashMap, the result will be a number of the n-power of 2 that is a little larger than the specified number. The method for calculating the length of the array is actually the following source code:
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
The code above uses a lot of bit operations. No matter what it is, if you call this method, you will verify the statement that the upper 2 is n-power. In addition, the subtraction of one in the first line of the above method is actually to avoid generating a number greater than the n-power of 2 when the incoming number is just the n-power of 2.
Why does this length have to be the n-th power of 2? The conclusion is to reduce hash collision, because in the above putVal method, we can see that the value of the underlying array index is actually the following code:
if ((p = tab[i = (n - 1) & hash]) == null)
In other words, the index is calculated by an expression such as "(n - 1) & hash", which is equivalent to "hash% n".
To put it simply, the index of the underlying array of HashMap is determined through the hash value of key and the remainder operation of array length. In this operation, n is the array length. When the value of n is the power of 2, the same probability can be reduced (note that n here is a variable in HashMap and cannot be confused with the n power of 2).
The so-called hash collision in HashMap actually means that the values of this array index are equal.
When the values are really equal, that is, to store data in the same position of the array, it's the linked list's turn to play a role. This part of the code is in putVal above.
First, judge whether the hash values of the two keys are the same and whether the key values are the same. If the two keys are the same, it is determined that they are the same. If they are different, it is determined whether they are red black tree structure. If so, create a new tree node. If not, follow the logic of linked list.
Here, whether the hash value is the same as the judgment value involves the hashCode method and equals method of the object. Therefore, for the object that needs to be the key of the HashMap, you need to rewrite the hashCode and equals methods.
In the logic of the linked list, there is also the logic that the linked list is transformed into a red black tree structure, that is:
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
...
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
Combing the logic above, we can see that there is a key judgment, "bincount > = tree_threshold - 1" and "(n = tab. Length) < min_tree_capability", where tree_ Threshold is 8, min_ TREEIFY_ The capability is 64. By analyzing this part of the code, we can know that the linked list will be converted to a red black tree structure only when the length of the linked list is greater than 8 and the length of the array is greater than 64. It is said that the jdk R & D team has tested and found that the performance is better after conversion in such cases.
The specific content of red black tree is complex. What we need to remember here is that it is a relatively balanced binary search tree. In fact, it is also to improve query performance.
LinkedHashMap
Because HashMap determines the array subscript according to the hash value hash algorithm, the storage order of the stored elements cannot be guaranteed, and HashMap has a subclass LinkedHashMap. On this basis, LinkedHashMap adds a linked list to store the storage order of the elements. Other contents are basically similar to HashMap.
TreeMap
TreeMap stores key value pairs directly based on the red black tree. When saving data, you need to compare the size of keys. This comparison can be made with the help of object comparators, either external comparators or internal comparators. When creating TreeMap objects, you can choose to pass in external comparators.
In the process of storing data, the root node of the red black tree will change to try to maintain a so-called balance. The reason for balancing is to find faster, because the search will be based on the comparator and the key of the node. If it is small, look to the left of the root node; if it is large, look to the right of the root node. Try to balance both sides, It may reduce the number of queries and improve the efficiency. The relevant source code is as follows:
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
In fact, when saving data, it is the same way to judge the size of the key, so as to judge whether to put it forward to the left or to the right, but it is not just judged with the root node, and finally the balance and color of the red black tree should be adjusted. The relevant source code is as follows:
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
```