Portal

Official explanation (Very well spoken)

Solution: We put all the land in a row, which can be well converted into an interval problem, asking each interval [L,R] for the value of the land and the conditions. For a land to be eligible, the land it can reach must be outside the questioning interval or not exist. This means that the nearest land x to its left (satisfying condition x < L, there is no reachable land x=0) and the nearest land y to its right (satisfying condition Y > R, there is no reachable land y=n+1).
The above conditions can be transformed into a three-dimensional numerical point problem.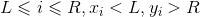The vegetable value of the land under these conditions.

We write it down as _____________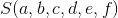 To satisfyThe sum of the vegetable value of the land.
The answer we see as _____________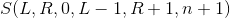

Using tolerance exclusion principle (similar to two dimensional prefix and rectangle area)

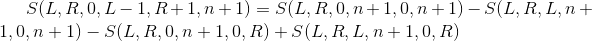
Formula 1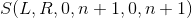It is an interval and (prefix and fix).

Formula 2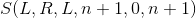All you need to do is satisfy .

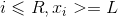Formula 3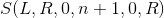All you need to do is satisfy .

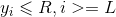Formula 4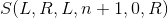All you need to do is satisfy .

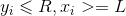It can be found that the three-dimensional point problem can be transformed into three two-dimensional point problems. All queries are offline, ordered according to the first dimension. The second dimension is the subscript and scanned sequentially. When a point encounters a point, it adds its position corresponding to the second dimension with its weight. When it encounters a query, it inquires the corresponding interval sum corresponding to the second dimension. Only one number supports single point addition and interval summation. According to the structure, the tree array can be competent.

Code:

#include<bits/stdc++.h>
#define lowbit(x)   (x&(-x))
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 5;
int read() {
    int x = 0, w = 1;
    char ch = 0;
    while (ch < '0' || ch > '9') {
        if (ch == '-') w = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') { x = x * 10 + (ch - '0'), ch = getchar(); }
    return x * w;
}
int n, m, q;
int x[maxn], y[maxn], a[maxn], pre[maxn];
int ans[maxn];
ll low[maxn];
struct node {
    int l, r, id, add;
} Q[maxn], temp[maxn << 1];
bool cmp(node a, node b) { return a.l == b.l ? a.id < b.id : a.l > b.l; }
void add(int i, int add) {
    if (i == 0) return;
    while (i <= n) { low[i] += add, i += lowbit(i); }
}
ll sum(int i) {
    ll all = 0;
    while (i > 0) { all += low[i], i -= lowbit(i); }
    return all;
}
/// L<=x[i],i<=R
void solve_1() {
    for (int i = 0; i <= n + 1; i++)low[i] = 0;
    for (int i = 1; i <= q; i++)temp[i] = Q[i];
    for (int i = 1; i <= n; i++)temp[i + q] = node{x[i], i, 0, a[i]};
    sort(temp + 1, temp + 1 + n + q, cmp);
    for (int i = 1; i <= n + q; i++) {
        if (temp[i].id)ans[temp[i].id] -= sum(temp[i].r);
        else add(temp[i].r, temp[i].add);
    }
}
/// L<=i y[i]<=R
void solve_2() {
    for (int i = 0; i <= n + 1; i++)low[i] = 0;
    for (int i = 1; i <= q; i++)temp[i] = Q[i];
    for (int i = 1; i <= n; i++)temp[i + q] = node{i, y[i], 0, a[i]};
    sort(temp + 1, temp + 1 + n + q, cmp);
    for (int i = 1; i <= n + q; i++) {
        if (temp[i].id)ans[temp[i].id] -= sum(temp[i].r);
        else add(temp[i].r, temp[i].add);
    }
}
///L<=x[i] y[i]<=R
void solve_3() {
    for (int i = 0; i <= n + 1; i++)low[i] = 0;
    for (int i = 1; i <= q; i++)temp[i] = Q[i];
    for (int i = 1; i <= n; i++)temp[i + q] = node{x[i], y[i], 0, a[i]};
    sort(temp + 1, temp + 1 + n + q, cmp);
    for (int i = 1; i <= n + q; i++) {
        if (temp[i].id)ans[temp[i].id] += sum(temp[i].r);
        else add(temp[i].r, temp[i].add);
    }
}
int main() {
    n = read(), m = read(), q = read();
    for (int i = 1; i <= n; i++) {
        a[i] = read();
        pre[i] = pre[i - 1] + a[i];
        x[i] = 0, y[i] = n + 1;
    }
    int u, v;
    for (int i = 1; i <= m; i++) {
        u = read(), v = read();
        if (u > v)x[u] = max(x[u], v);
        else y[u] = min(y[u], v);
    }
    for (int i = 1; i <= q; i++) {
        Q[i].l = read();
        Q[i].r = read();
        ans[i] = pre[Q[i].r] - pre[Q[i].l - 1];
        Q[i].id = i;
    }
    solve_1(), solve_2(), solve_3();
    ll all = 0;
    for (int i = 1; i <= q; i++) all = all ^ (1LL * ans[i] * i);
    printf("%lld\n", all);
    return 0;
}