✨ preface ✨
📘 Blog home page: to Keep blog home page
🙆 Welcome to pay attention, 👍 give the thumbs-up, 📝 Message comments
⏳ Starting time: March 1, 2022
📨 Blogger code cloud address: Blogger code cloud address
📕 Reference book: java core technology Volume 1
📢 Programming exercises: Niuke network+Force buckle net
As the blogger is also in a state of learning, if there is something wrong, please contact me to correct it!!!
🚄 1 quick sort
🚅 1.1 fast exhaust principle
1 select a number from the range to be sorted as the benchmark value
2. Traverse the whole range to be sorted, put the smaller (can contain equal) than the benchmark value to the left of the benchmark value, and put the larger (can contain equal) than the benchmark value to the right of the benchmark value;
3. Divide and conquer the left and right cells and the left and right cells in the same way until the length of the cells = = 1, then the surface is orderly. If the length is zero, it means there is no data!
🚈 1.2 recursive implementation
By understanding the principle of fast scheduling, we can write the following code (at the beginning, we take the first number in the sequence as the benchmark value to find the position of the benchmark in the sequence):
public class TestDemo1 {
public static void main(String[] args) {
int[] array = {67,7,32,98,1,0,45,23,234,6746,123};
Quack(array);
System.out.println(Arrays.toString(array));
}
/**
* Fast row recursive writing
* Time complexity: best O(N*logN) worst (ordered) O(N*N)
* Space complexity: O(logN)
* Stability: unstable
* @param array Sequence to be sorted
*/
public static void Quack(int[] array){
QuackSort(array,0,array.length-1);
}
public static void QuackSort(int[] array,int left,int right){
//The termination condition of recursion. When the left is equal to or greater than the right, it indicates that the sequence is orderly at this time
if(left>=right){
return;
}
//Find benchmark
int privot = getprivot(array,left,right);
//Recursive left
QuackSort(array,left,privot-1);
//Recursive right
QuackSort(array,privot+1,right);
}
public static int getprivot(int[] array,int start,int end){
int tmp = array[start];
while (start<end){
while (start<end&&array[end]>=tmp){
end--;
}
array[start]=array[end];
while (start<end&&array[start]<=tmp){
start++;
}
array[end]=array[start];
}
array[start]=tmp;
return start;
}
}
🚝 1.3 optimize the fast platoon (three digit centering method)
The optimization of fast exhaust is actually the optimization benchmark:
public class TestDemo1 {
public static void main(String[] args) {
int[] array = {67,7,32,98,1,0,45,23,234,6746,123};
Quack(array);
System.out.println(Arrays.toString(array));
}
/**
* Fast row recursive writing
* Time complexity: best O(N*logN) worst (ordered) O(N*N)
* Space complexity: O(logN)
* Stability: unstable
* @param array
*/
public static void Quack(int[] array){
QuackSort(array,0,array.length-1);
}
public static void Swap(int[] array,int i,int j){
int tmp = array[i];
array[i]=array[j];
array[j]=tmp;
}
public static int getMid(int[] array,int a,int b){
int mid = a+((b-a)>>>1);
if(array[a]>array[b]){
if(array[mid]>array[a]){
return a;
}else if(array[mid]<array[b]){
return b;
}else{
return mid;
}
}else{//array[a]<array[b]
if(array[mid]<array[a]){
return a;
}else if(array[mid]>array[b]){
return b;
}else{
return mid;
}
}
}
public static void QuackSort(int[] array,int left,int right){
//The termination condition of recursion. When the left is equal to or greater than the right, it indicates that the sequence is orderly at this time
if(left>=right){
return;
}
//Gets the subscript of the middle value of three values
int mid = getMid(array,left,right);
//Put the middle value at the beginning
Swap(array,left,mid);
//Find benchmark
int privot = getprivot(array,left,right);
//Recursive left
QuackSort(array,left,privot-1);
//Recursive right
QuackSort(array,privot+1,right);
}
public static int getprivot(int[] array,int start,int end){
int tmp = array[start];
while (start<end){
while (start<end&&array[end]>=tmp){
end--;
}
array[start]=array[end];
while (start<end&&array[start]<=tmp){
start++;
}
array[end]=array[start];
}
array[start]=tmp;
return start;
}
}
Optimization summary:
1. The optimization of fast scheduling is essentially the optimization of the benchmark, so the three digit centring method is used for optimization
2. It can be optimized in combination with the direct insertion sort we learned before. For the insertion sort, we have learned that the more ordered the sequence is, the faster it is. Then, when the adjusted length is less than a certain number, we can directly use the direct insertion sort
🚃 1.4 non recursive implementation
For non recursive implementation, we still need to find the benchmark value according to the principle, and then use the stack in the data structure to solve it (the core idea is to use benchmark to solve it):
The code is as follows:
//Non recursive implementation
public static void nonQuackSort(int[] array){
int start = 0;
int end = array.length-1;
Stack<Integer> stack = new Stack<>();
//Find benchmark
int privot = getprivot(array,start,end);
//Make sure there are at least two sortable numbers on the right, otherwise there is only one number, which is ordered
if(privot-1>start){
stack.push(start);
stack.push(privot-1);
}
//Make sure there are at least two sortable numbers on the left, otherwise there is only one number, which is ordered
if(privot+1<end){
stack.push(privot+1);
stack.push(end);
}
while (!stack.isEmpty()){
end=stack.pop();
start=stack.pop();
privot = getprivot(array,start,end);
if(privot-1>start){
stack.push(start);
stack.push(privot-1);
}
if(privot+1<end){
stack.push(privot+1);
stack.push(end);
}
}
}
🚋 Binary merge sort
🚌 2.1 core idea of merger
Given two ordered arrays, how do you combine them into an ordered array? In fact, in the process of merger, it reflects the preliminary thought and principle of merging and sorting, which is based on such an idea.
The code is as follows:
public static int[] conbine(int[] array1,int[] array2){
//Create a new array to store the merged data
int[] array = new int[array1.length+array2.length];
//Subscript of record merge array
int i = 0;
//First subscript of the first array
int s1 = 0;
//The last subscript of the first array
int e1 = array1.length-1;
//The first subscript of the second array
int s2 = 0;
//The last subscript of the second array
int e2 = array2.length-1;
//Put the data in the two arrays into the new array from small to large
while (s1<=e1&&s2<=e2){
if(array1[s1]<array2[s2]){
array[i++]=array1[s1++];
}else{
array[i++]=array2[s2++];
}
}
//The first array may not be finished or the data of the second array may not be finished
while (s1<=e1){
array[i++]=array1[s1++];
}
while (s2<=e2){
array[i++]=array2[s2++];
}
return array;
}
🚎 2.2 recursive implementation of merge sort
public static void mergeSort(int[] array){
merge(array,0,array.length-1);
}
public static void merge(int[] array,int low,int high){
int mid = low+((high-low)>>>1);
//Termination condition of recursion
if(low>=high){
return;
}
//Recursive decomposition on the left
merge(array,low,mid);
//Recursive decomposition on the right
merge(array,mid+1,high);
//Start merging
Conbine(array,low,mid,high);
}
//The core idea of merging
public static void Conbine(int[] array,int low,int mid,int high){
int[] tmp = new int[high-low+1];
int i = 0;
int s1 = low;
int e1 = mid;
int s2 = mid+1;
int e2 = high;
while (s1<=e1&&s2<=e2){
while (s1<=e1&&s2<=e2){
if(array[s1]<array[s2]){
tmp[i++]=array[s1++];
}else{
tmp[i++]=array[s2++];
}
}
//The first array may not be finished or the data of the second array may not be finished
while (s1<=e1){
tmp[i++]=array[s1++];
}
while (s2<=e2){
tmp[i++]=array[s2++];
}
}
for (int j = 0; j < i; j++) {
//Pay attention to the array subscript. When the right array is merged, its first subscript is no longer zero
array[j+low]=tmp[j];
}
}
🚍 2.3 non recursive implementation of merge sort
The idea of non recursive sorting is to group first, one by one. When it becomes a group of two, and finally the whole array is a group, it is an ordered array at this time.
public static void nonmergeSort(int[] array){
//Number of groups (one group at the beginning)
int gap = 1;
//Only when the number of groups is greater than or equal to the length of the array, it indicates that the array has been ordered
while (gap<array.length){
//After each regrouping, traverse the array and merge and sort
for (int i = 0; i < array.length-1; i+=2*gap) {
int left = i;
int mid = left+gap-1;
//Note that the mid may cross the boundary at this time
if (mid>=array.length){
mid=array.length-1;
}
int right = mid+gap;
if(right>=array.length){
right=array.length-1;
}
//Start merging
Conbine(array,left,mid,right);
}
//At the end of the cycle, multiply the number of groups by 2
gap=gap*2;
}
}
public static void Conbine(int[] array,int low,int mid,int high){
int[] tmp = new int[high-low+1];
int i = 0;
int s1 = low;
int e1 = mid;
int s2 = mid+1;
int e2 = high;
while (s1<=e1&&s2<=e2){
while (s1<=e1&&s2<=e2){
if(array[s1]<array[s2]){
tmp[i++]=array[s1++];
}else{
tmp[i++]=array[s2++];
}
}
//The first array may not be finished or the data of the second array may not be finished
while (s1<=e1){
tmp[i++]=array[s1++];
}
while (s2<=e2){
tmp[i++]=array[s2++];
}
}
for (int j = 0; j < i; j++) {
//Pay attention to the array subscript. When the right array is merged, its first subscript is no longer zero
array[j+low]=tmp[j];
}
}
🚗 III. other sorting (not based on comparison)
🚖 3.1 counting and sorting
Detailed explanation of counting and sorting
🚘 3.2 cardinality sorting
Detailed explanation of cardinality sorting
🚔 3.3 bucket sorting
Detailed explanation of bucket sorting
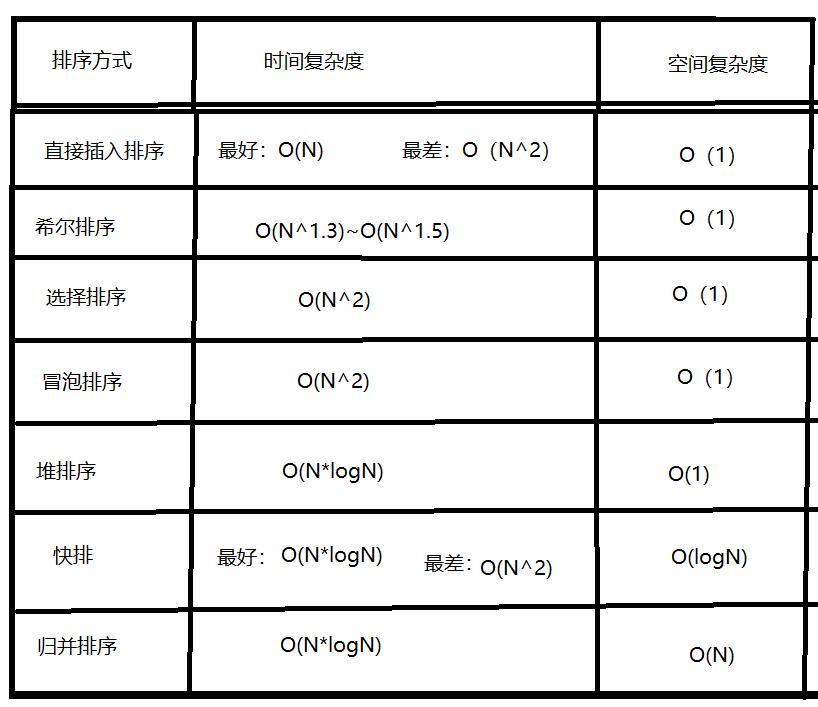
🚉 4 Summary
You can list the characteristics of these sorting through a table, and select the appropriate sorting method according to the sorting requirements!