Common loss function learning essays

• Learning objectives
• Know the loss function of classification task
• Know the loss function of the regression task

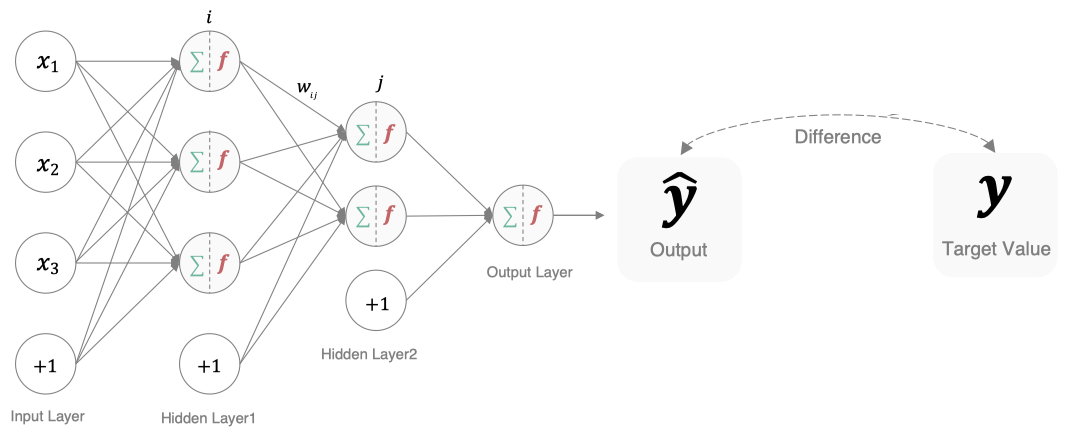
In deep learning, loss function is a function used to measure the quality of model parameters. The measurement method is to compare the difference between network output and real output. The names of loss function are different in different literatures. There are mainly the following naming methods:

Classification task

The cross entropy loss function is most used in the classification task of deep learning, so we focus on this loss function here.

Multi classification task

In multi classification tasks, softmax is usually used to convert logits into probability, so the cross entropy loss of multi classification is also called softmax loss. Its calculation method is:

Where y is the true probability that sample x belongs to a certain category, f(x) is the prediction score of sample belonging to a certain category, S is the softmax function, and L is used to measure the loss result of the difference between P and Q.

example:

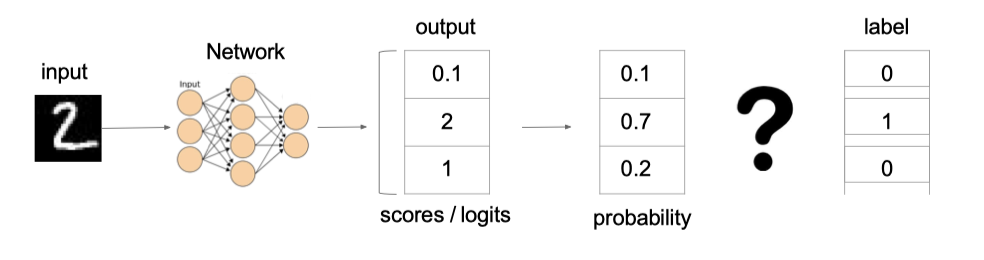
The cross entropy loss in the figure above is:

From the perspective of probability, our purpose is to minimize the negative value of the logarithm of the prediction probability corresponding to the correct category, as shown in the figure below:

In TF Keras is implemented using CategoricalCrossentropy, as shown below:

# Import the corresponding package
import tensorflow as tf
# Set true and predicted values
y_true = [[0, 1, 0], [0, 0, 1]]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
# Instantiation cross entropy loss
cce = tf.keras.losses.CategoricalCrossentropy()
# Calculation of loss results
cce(y_true, y_pred).numpy()

The result is:

1.176939

II. Classification tasks

When dealing with the second classification task, we no longer use the softmax activation function, but the sigmoid activation function. The loss function is adjusted accordingly, and the cross entropy loss function of the second classification is used:

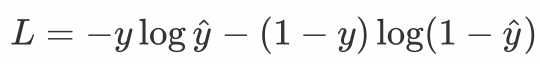
Where y is the true probability that sample x belongs to a certain category, and Y ^ is the prediction probability that sample belongs to a certain category. L is used to measure the loss result of the difference between the true value and the predicted value.

In TF BinaryCrossentropy() is used for implementation in keras, as shown below:

# Import the corresponding package
import tensorflow as tf
# Set true and predicted values
y_true = [[0], [1]]
y_pred = [[0.4], [0.6]]
# Instantiation cross entropy classification
bce = tf.keras.losses.BinaryCrossentropy()
# Calculation of loss results
bce(y_true, y_pred).numpy()

The result is:

0.5108254

Return task

The loss functions commonly used in regression tasks are as follows:

MAE loss

Mean absolute loss(MAE), also known as L1 Loss, takes the absolute error as the distance:

The curve is shown in the figure below:

The characteristic is that L1 loss is sparse. In order to punish large values, it is often added to other losses as a regular term as a constraint. The biggest problem with L1 loss is that the gradient is not smooth at zero, resulting in skipping the minimum.

In TF The implementation of MeanAbsoluteError in keras is as follows:

# Import the corresponding package
import tensorflow as tf
# Set true and predicted values
y_true = [[0.], [0.]]
y_pred = [[1.], [1.]]
# Instantiation MAE loss
mae = tf.keras.losses.MeanAbsoluteError()
# Calculation of loss results
mae(y_true, y_pred).numpy()

The result is:

1.0

MSE loss

Mean Squared Loss/ Quadratic Loss(MSE loss), also known as L2 loss, or Euclidean distance, takes the sum of squares of errors as the distance:

The curve is shown in the figure below:

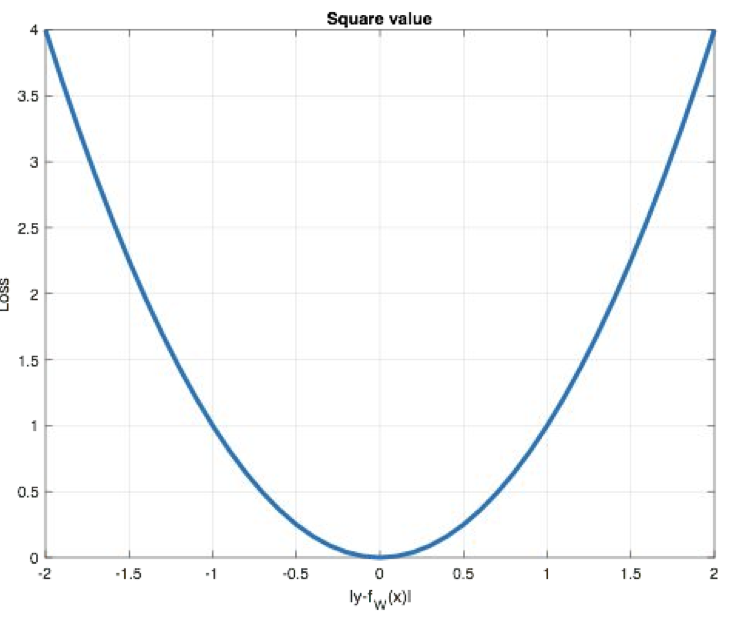
The characteristic is that L2 loss is often used as a regular term. When the predicted value is very different from the target value, the gradient is easy to explode.

In TF In keras, it is realized through meansquareerror:

# Import the corresponding package
import tensorflow as tf
# Set true and predicted values
y_true = [[0.], [1.]]
y_pred = [[1.], [1.]]
# Instantiation MSE loss
mse = tf.keras.losses.MeanSquaredError()
# Calculation of loss results
mse(y_true, y_pred).numpy()

The result is:

0.5

smooth L1 loss

Smooth L1 loss function is as follows:

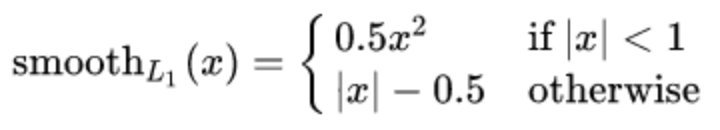
Where: 𝑥 = f(x) − y is the difference between the real value and the predicted value.

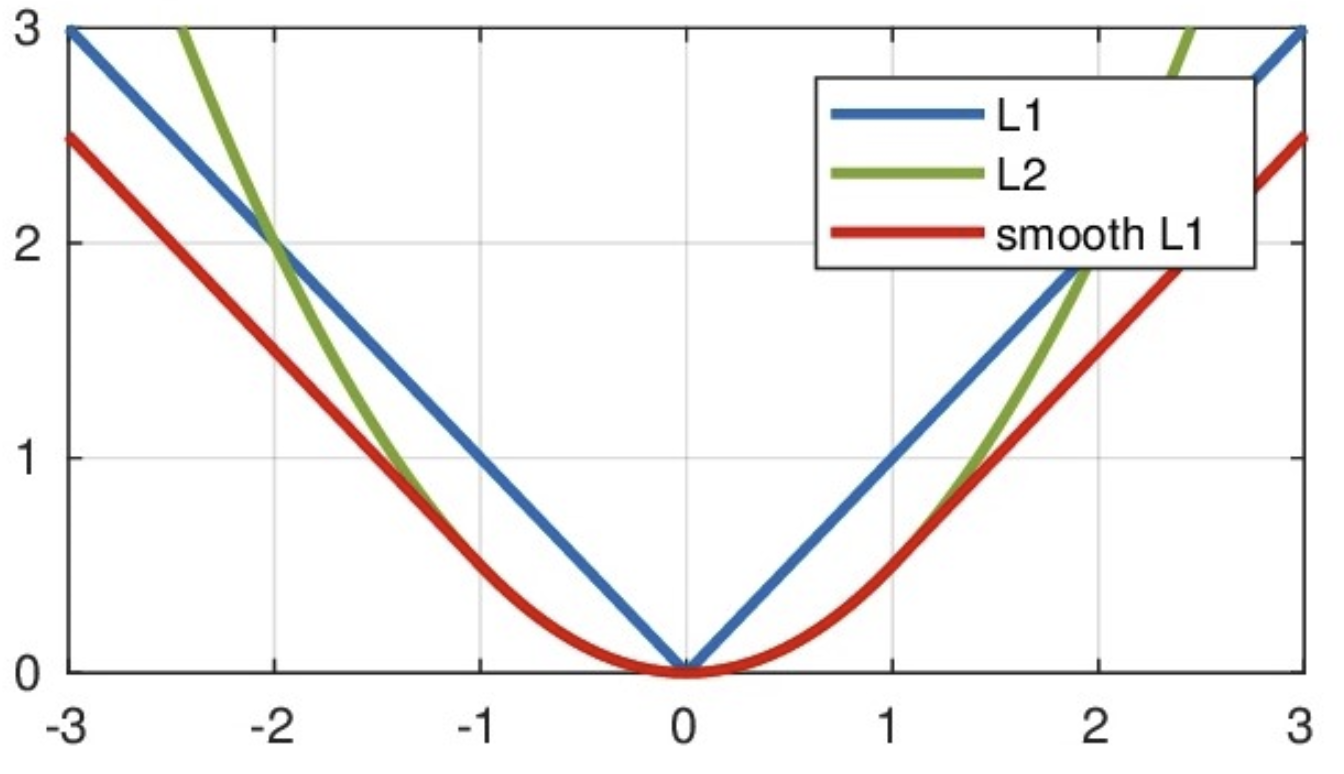
As can be seen from the above figure, this function is actually a piecewise function. Between [- 1,1], it is actually L2 loss, which solves the problem of L1 unsmoothness. Outside the interval [- 1,1], it is actually L1 loss, which solves the problem of outlier gradient explosion. This loss function is usually used in target detection.

In TF Huber is used in keras to calculate this loss as follows:

# Import the corresponding package
import tensorflow as tf
# Set true and predicted values
y_true = [[0], [1]]
y_pred = [[0.6], [0.4]]
# Instantiation smooth L1 loss
h = tf.keras.losses.Huber()
# Calculation of loss results
h(y_true, y_pred).numpy()

result:

0.18

summary

• Know the loss function of classification task

Cross entropy loss function of multi classification and cross entropy loss function of two classification

• Know the loss function of the regression task

MAE, MSE, smooth L1 loss function