K-L (Kernighan Lin) algorithm
Original paper( An efficient heuristic procedure for partitioning graphs)
K-L (Kernighan Lin) algorithm is a dichotomy method that divides a known network into two communities of known size. It is a greedy algorithm.
Its main idea is to define a function gain Q for network partition.
Q is the difference between the number of sides within the community and the number of sides between the communities.
According to this method, we find a method to divide the community so that the value of gain function Q becomes the maximum value.
The specific strategy is to move the nodes in the community structure to other community structures or exchange the nodes in different community structures. Search from the initial solution until no better candidate solution can be found from the current solution, and then stop.
Firstly, the nodes of the whole network are divided into two parts randomly or according to the existing information of the network. All possible node pairs are considered between the two communities, each pair of nodes is tentatively exchanged, and the data before and after the exchange are calculated Δ Q, Δ Q = after Q exchange - before Q exchange, record Δ The exchange node pair with the largest Q, exchange the two nodes, and record the Q value at this time.
It is stipulated that each node can only be exchanged once, and this process is repeated until all nodes in the network are exchanged once. It should be noted that it cannot be stopped when the Q value decreases, because the Q value does not increase monotonically. Even if the Q value will decrease in one step of exchange, a larger Q value may appear in the subsequent step of exchange. After all nodes have been exchanged, the community structure with the largest corresponding Q value is considered to be the ideal community structure of the network.
The defect of K-L algorithm is that the size of two subgraphs must be specified first, otherwise the correct results will not be obtained, which is of little practical significance.
The Python code is as follows:
import networkx as nx
import matplotlib.pyplot as plt
from networkx.algorithms.community import kernighan_lin_bisection
def draw_spring(G, com):
"""
G:chart
com: Divided communities
node_size Indicates the size of the node
node_color Represents the node color
node_shape Represents the shape of a node
with_labels=True Indicates whether the node is labeled
"""
pos = nx.spring_layout(G) # The layout of nodes is spring type
NodeId = list(G.nodes())
node_size = [G.degree(i) ** 1.2 * 90 for i in NodeId] # Node size
plt.figure(figsize=(8, 6)) # Picture size
nx.draw(G, pos, with_labels=True, node_size=node_size, node_color='w', node_shape='.')
color_list = ['pink', 'orange', 'r', 'g', 'b', 'y', 'm', 'gray', 'black', 'c', 'brown']
# node_shape = ['s','o','H','D']
for i in range(len(com)):
nx.draw_networkx_nodes(G, pos, nodelist=com[i], node_color=color_list[i])
plt.show()
if __name__ == "__main__":
G = nx.karate_club_graph() # karate club
# KL algorithm
com = list(kernighan_lin_bisection(G))
print('Number of communities', len(com))
print(com)
draw_spring(G, com)
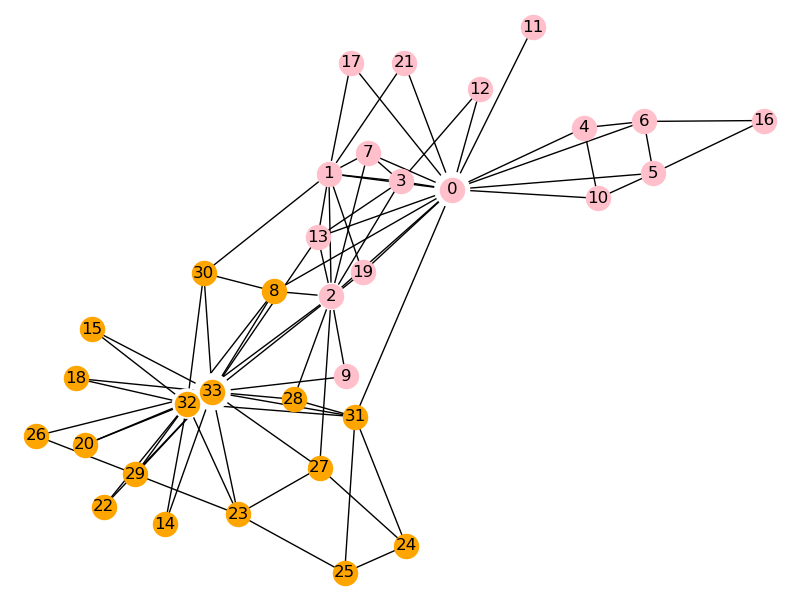
The kl algorithm in networkx library is directly used here. The data set Zachary karate club network is a social network constructed by observing an American University karate club The network consists of 34 nodes and 78 edges, in which the individual represents the members of the club and the edge represents the friendship between the members Karate club network has become a classic problem in the detection of complex network community structure.
After one time, the kl algorithm is divided into two parts as shown in the figure.
The codes and data sets related to community division are placed in github , you can download it yourself.
The specific kl algorithm is as follows. It is the algorithm in networkx library. You can refer to the following:
"""Functions for computing the Kernighan–Lin bipartition algorithm."""
import networkx as nx
from itertools import count
from networkx.utils import not_implemented_for, py_random_state, BinaryHeap
from networkx.algorithms.community.community_utils import is_partition
__all__ = ["kernighan_lin_bisection"]
def _kernighan_lin_sweep(edges, side):
"""
This is a modified form of Kernighan-Lin, which moves single nodes at a
time, alternating between sides to keep the bisection balanced. We keep
two min-heaps of swap costs to make optimal-next-move selection fast.
"""
costs0, costs1 = costs = BinaryHeap(), BinaryHeap()
for u, side_u, edges_u in zip(count(), side, edges):
cost_u = sum(w if side[v] else -w for v, w in edges_u)
costs[side_u].insert(u, cost_u if side_u else -cost_u)
def _update_costs(costs_x, x):
for y, w in edges[x]:
costs_y = costs[side[y]]
cost_y = costs_y.get(y)
if cost_y is not None:
cost_y += 2 * (-w if costs_x is costs_y else w)
costs_y.insert(y, cost_y, True)
i = totcost = 0
while costs0 and costs1:
u, cost_u = costs0.pop()
_update_costs(costs0, u)
v, cost_v = costs1.pop()
_update_costs(costs1, v)
totcost += cost_u + cost_v
yield totcost, i, (u, v)
@py_random_state(4)
@not_implemented_for("directed")
def kernighan_lin_bisection(G, partition=None, max_iter=10, weight="weight", seed=None):
"""Partition a graph into two blocks using the Kernighan–Lin
algorithm.
This algorithm partitions a network into two sets by iteratively
swapping pairs of nodes to reduce the edge cut between the two sets. The
pairs are chosen according to a modified form of Kernighan-Lin, which
moves node individually, alternating between sides to keep the bisection
balanced.
Parameters
----------
G : graph
partition : tuple
Pair of iterables containing an initial partition. If not
specified, a random balanced partition is used.
max_iter : int
Maximum number of times to attempt swaps to find an
improvemement before giving up.
weight : key
Edge data key to use as weight. If None, the weights are all
set to one.
seed : integer, random_state, or None (default)
Indicator of random number generation state.
See :ref:`Randomness<randomness>`.
Only used if partition is None
Returns
-------
partition : tuple
A pair of sets of nodes representing the bipartition.
Raises
-------
NetworkXError
If partition is not a valid partition of the nodes of the graph.
References
----------
.. [1] Kernighan, B. W.; Lin, Shen (1970).
"An efficient heuristic procedure for partitioning graphs."
*Bell Systems Technical Journal* 49: 291--307.
Oxford University Press 2011.
"""
n = len(G)
labels = list(G)
seed.shuffle(labels)
index = {v: i for i, v in enumerate(labels)}
if partition is None:
side = [0] * (n // 2) + [1] * ((n + 1) // 2)
else:
try:
A, B = partition
except (TypeError, ValueError) as e:
raise nx.NetworkXError("partition must be two sets") from e
if not is_partition(G, (A, B)):
raise nx.NetworkXError("partition invalid")
side = [0] * n
for a in A:
side[a] = 1
if G.is_multigraph():
edges = [
[
(index[u], sum(e.get(weight, 1) for e in d.values()))
for u, d in G[v].items()
]
for v in labels
]
else:
edges = [
[(index[u], e.get(weight, 1)) for u, e in G[v].items()] for v in labels
]
for i in range(max_iter):
costs = list(_kernighan_lin_sweep(edges, side))
min_cost, min_i, _ = min(costs)
if min_cost >= 0:
break
for _, _, (u, v) in costs[: min_i + 1]:
side[u] = 1
side[v] = 0
A = {u for u, s in zip(labels, side) if s == 0}
B = {u for u, s in zip(labels, side) if s == 1}
return A, B