LPA(Label Propagation Algorithm)

LPA algorithm was proposed by zhu et al in 2002. In 2007, it was applied to the field of community discovery by Usha, Nandini and Raghavan, and RAK algorithm was proposed. But most researchers call RAK algorithm LPA algorithm.

LPA is a local community division based on Label Propagation. For each node in the network, in the initial stage, the Label Propagation algorithm initializes a unique label for each node. Each iteration will change its own label according to the label of the node connected to it. The principle of change is to select the community label with the most labels among the nodes connected to it as its own community label, which is the meaning of Label Propagation. As community labels continue to spread. Finally, closely connected nodes will have common labels.

LPA believes that the label of each node should be the same as that of most of its neighbors, and takes the largest number of labels in the label of a node's neighbor node as the label of the node itself (bagging idea). Add a label to each node to represent the community it belongs to, and form the same "community" through the "propagation" of the label, which has the same "label" inside.

The label propagation algorithm (LPA) is simple:

Step 1: assign a unique label to all nodes;

Step 2: refresh the labels of all nodes round by round until the convergence requirements are met. For each round of refresh, the rules for node label refresh are as follows:

For a node, investigate the labels of all its neighbor nodes, make statistics, and assign the label with the largest number to the current node. When the largest number of tags are not unique, choose one at random.

A simple example of LPA

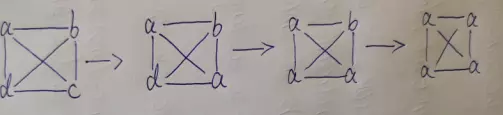
**Algorithm initialization: * * a, b, c and d are independent communities;

First round of label dissemination:

At the beginning, c chose a, because everyone's community tags are the same, so I randomly chose one;

d also determines the number of tags according to its surrounding neighbor nodes. The largest is a, so d is a;

**Continue label propagation: * * and so on, and finally all are a;

The time complexity is nearly linear: the complexity of assigning labels to vertices is O(n), the time of each iteration is O (m), and the complexity of finding all communities is O (n +m), but the number of iterations is difficult to estimate

LPA tag propagation can be divided into two modes: synchronous update and asynchronous update.

1. Synchronize updates

The so-called synchronous update means that the label of node z in iteration t is based on the label obtained by its neighbor node in iteration t-1.

For node x, during the t-th iteration, it is updated according to the label of its node in generation t-1. that is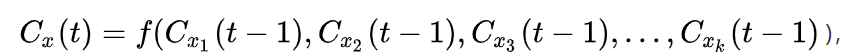

, where C x ( t ) C_x(t) Cx (t) represents the community label of node x in the t-th iteration. The function f represents the one with the most community tags in the parameter node.

It should be noted that there is a problem with this synchronous update method. When a bipartite graph is encountered, there will be label oscillation. The solution is to set the maximum number of iterations and stop the iterations in advance.

2. Asynchronous update

That is, the label of node z in iteration t is based on the label of the node that has updated the label in iteration T and the label of the node that has not updated the label in iteration t-1.

Advantages and disadvantages of LPA algorithm

The biggest advantage of LPA algorithm is that the logic of the algorithm is very simple, and the process of optimizing the modular algorithm is very fast.

LPA algorithm uses its own network structure to guide label propagation. This process does not need any optimization function, and it does not need to know the number of communities before the initialization of the algorithm. With the iteration of the algorithm, you can know the final number of communities.

The disadvantage of this algorithm is that it is not stable. Specifically reflected in:

1. Each vertex is given a unique label at the beginning, that is, the "importance" is the same, and the iterative process adopts a random sequence. The update order of node labels is random, which will lead to different results in the same initial state and even the emergence of giant communities;
2. Random selection: if there is more than one neighbor label with the largest number of occurrences of a node, randomly select one label as its own label. This randomness may bring an avalanche effect, that is, a small clustering error will be amplified at the beginning. However, if there are multiple similar neighbor nodes, there may be a problem with the logic of weight calculation. We need to go back and optimize the weight abstraction and calculation logic.

The code is as follows:

class LPA:
    def __init__(self, G, max_iter=20):
        self._G = G
        self._n = len(G.nodes(False))  # Number of nodes
        self._max_iter = max_iter

    # Judge whether convergence
    def can_stop(self):
        # The label of each node is the same as that of the most adjacent nodes
        for i in range(self._n):
            node = self._G.nodes[i]
            label = node["label"]
            max_labels = self.get_max_neighbor_label(i)
            if label not in max_labels:
                return False
        return True

    # Get the most labels of adjacent nodes
    def get_max_neighbor_label(self, node_index):
        m = collections.defaultdict(int)
        for neighbor_index in self._G.neighbors(node_index):
            neighbor_label = self._G.nodes[neighbor_index]["label"]
            m[neighbor_label] += 1
        max_v = max(m.values())
        # The number of multiple tags may be the same, and they all need to be returned here
        return [item[0] for item in m.items() if item[1] == max_v]

    # Asynchronous update
    def populate_label(self):
        # Random access
        visitSequence = random.sample(self._G.nodes(), len(self._G.nodes()))
        for i in visitSequence:
            node = self._G.nodes[i]
            label = node["label"]
            max_labels = self.get_max_neighbor_label(i)
            # If the label is not in the maximum label set, it will be updated, otherwise the same random selection is meaningless
            if label not in max_labels:
                newLabel = random.choice(max_labels)
                node["label"] = newLabel

    # Get the community structure according to the label
    def get_communities(self):
        communities = collections.defaultdict(lambda: list())
        for node in self._G.nodes(True):
            label = node[1]["label"]
            communities[label].append(node[0])
        return communities.values()

    def execute(self):
        # Initialization label
        for i in range(self._n):
            self._G.nodes[i]["label"] = i
        iter_time = 0
        # Update label
        while (not self.can_stop() and iter_time < self._max_iter):
            self.populate_label()
            iter_time += 1
        return self.get_communities()

Improvement of LPA algorithm

1: Improvement of label random selection

Adding weights to nodes or edges (potential function, module density optimization, leaderank value, similarity of local topology information, label dependency coefficient, etc.), information entropy, etc. to describe the propagation priority of nodes, and then preliminarily determine the community center to improve the accuracy of community division;

In this way, when making the maximum label statistics of neighbor nodes, the weight weight of neighbor nodes and the degree of node adjacent nodes can be used as reference factors.

2: Tag initialization improvement

Some compact substructures can be extracted as the initial label for label propagation (such as non overlapping minimum maximum clique extraction algorithm), or the prototype of the community can be determined first through the initial community division algorithm.

3: Other possible improvements

1. In order to improve the stability and efficiency of the algorithm results, non overlapping triangles are found as the prototype of the initial cluster in the community;
2. Adding the tag entropy attribute, the random sequence is not used in the iterative process, but the sequence is sorted according to the tag entropy of each node;
3. On the basis of 2, in order to not completely eliminate the randomness of the label propagation algorithm, the sorted queue is divided into three parts, and the nodes are randomly arranged in each part.
4. For the label of the neighbor node of the same node, there may be the same maximum number of multiple communities. Instead of using the random method, analyze the label distribution of the neighbor node set of the neighbor node of the node to determine the label of the node
5. Look for the "snowflake" structure centered on several nodes with the largest degree in the community as the prototype of the initial cluster
   In the process of implementation, the above schemes are combined to derive more feasible schemes. The preliminary experimental results show that the randomness and stability of the algorithm are difficult to ensure at the same time. The structure of the initial cluster has fast convergence speed, but it is possible to generate giant communities; When there are few nodes, the method of label entropy has the best accuracy and stability; As for the combination scheme, the preliminary experimental verification found that the effect decreased.

SLPA(Speaker-listener Label Propagation Algorithm)

SLPA is an overlapping community discovery algorithm, which involves an important threshold parameter r. through the appropriate selection of r, it can be reduced to non overlapping

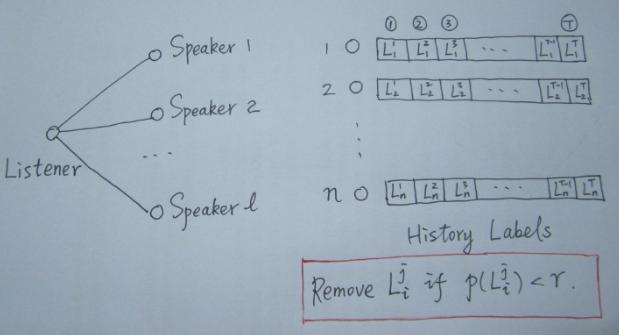
SLPA introduces two more vivid concepts of listener and speaker. You can understand it this way: in the process of refreshing the node label, select any node as a listener, then all its neighbor nodes are its speakers. There are usually more than one speaker. When a large group of speakers are talking, who should the listener listen to? Then we need to make a rule.

In LPA, we use the most frequent tags to make decisions. In fact, this is a rule. However, in the SLPA framework, there are many rules to select (which can be specified by the user).

Of course, compared with LPA, the biggest feature of SLPA is that it records the historical tag sequence of each node in the refresh iteration process (for example, if the iteration is t times, each node will save a sequence with length T, as shown in the figure above). When the iteration stops, the frequency of each (different) tag in each node's historical tag sequence is counted, According to a given threshold, those tags with low frequency are filtered out, and the rest are the tags of the node (usually multiple).

Algorithm steps

(1) Initialize the label information of all nodes so that each node has a unique label.
(2) The most important is the label dissemination process.

• The current node acts as a listener.
• Each neighbor node of the current node transmits label information according to a certain speaking strategy.
• The current node selects a label as the new label in this iteration according to a certain listener strategy in the label information set transmitted from the neighbor node.
• When the algorithm converges or traverses the specified number of times, the algorithm ends. Otherwise, the tag propagates in the process of continuous traversal.

(3) Label classification process. In the post-processing stage, community discovery is carried out according to the label information of the node.

Working process of SLPA:

1. Label all members differently
2. Traverse members and scan the tags of the members associated with each member.
3. The label record that appears the most times will become a candidate label for this member
4. The tag with the most candidate tags is the current community name of the member (for example, user 1 records the tag: 1 appears three times, 2 appears five times, 3 appears four times, and the community to which user 1 belongs is community 2)
5. After traversing the members for many times, the division of the community is more clear

Algorithm advantages

Algorithm SLPA will not forget the label information updated by nodes in the last iteration like other algorithms. It sets a label storage list for each node to store the updated labels in each iteration. The final membership of the node community will be determined by the probability of the tags observed in the tag storage list. When a node observes a lot of tags, it is likely that the node belongs to the community, and it is also likely to spread the tag to other nodes in the process of propagation. What's more, the design of this label storage list can enable the algorithm to support the division of overlapping communities.

Dolphin data set is a dolphin social relationship network obtained by D.Lusseau and others by observing the communication of 62 dolphin groups in the double sound Strait of New Zealand for up to 7 years. The network has 62 nodes and 159 sides. Nodes represent dolphins, while edges represent frequent contact between dolphins

The code is as follows:

class SLPA:
    def __init__(self, G, T, r):
        """
        :param G:Graph itself
        :param T: Number of iterations T
        :param r:Threshold for meeting community frequency requirements r
        """
        self._G = G
        self._n = len(G.nodes(False))  # Number of nodes
        self._T = T
        self._r = r

    def execute(self):
        # Node memory initialization
        node_memory = []
        for i in range(self._n):
            node_memory.append({i: 1})

        # Iterative process of algorithm
        for t in range(self._T):
            # Select any listener
            # np.random.permutation(): random permutation sequence
            order = [x for x in np.random.permutation(self._n)]
            for i in order:
                label_list = {}
                # Select a tag from the speaker and propagate it to the listener
                for j in self._G.neighbors(i):
                    sum_label = sum(node_memory[j].values())
                    label = list(node_memory[j].keys())[np.random.multinomial(
                        1, [float(c) / sum_label for c in node_memory[j].values()]).argmax()]
                    label_list[label] = label_list.setdefault(label, 0) + 1
                # listener selects one of the most popular tags to add to memory
                max_v = max(label_list.values())
                # selected_label = max(label_list, key=label_list.get)
                selected_label = random.choice([item[0] for item in label_list.items() if item[1] == max_v])
                # setdefault if the key does not exist in the dictionary, the key is added and the value is set to the default value.
                node_memory[i][selected_label] = node_memory[i].setdefault(selected_label, 0) + 1

        # Delete unqualified tags according to the threshold
        for memory in node_memory:
            sum_label = sum(memory.values())
            threshold_num = sum_label * self._r
            for k, v in list(memory.items()):
                if v < threshold_num:
                    del memory[k]

        communities = collections.defaultdict(lambda: list())
        # Scan the record labels in memory, and the nodes with the same label join the same community
        for primary, change in enumerate(node_memory):
            for label in change.keys():
                communities[label].append(primary)
        # The return value is a data dictionary. Value exists in the form of a set
        return communities.values()

give the result as follows

0 [1, 5, 6, 7, 9, 13, 17, 19, 22, 25, 26, 27, 31, 32, 39, 41, 48, 54, 56, 57]
1 [4, 8, 11, 15, 18, 21, 23, 24, 29, 35, 45, 51, 59]
2 [10, 28, 42, 47]
3 [12, 14, 16, 20, 33, 34, 37, 38, 40, 43, 44, 50, 52]
4 [60]
0.4337

Code and data download github