1, Sequential storage of binary tree

1. Storage mode
   Use the array to save the binary tree structure, that is, put the binary tree into the array by sequence traversal.
   Generally, it is only suitable for representing complete binary trees, because incomplete binary trees will waste space.
   The main use of this method is the representation of the heap

2. Subscript relation
   If the subscript of the parent is known, then:
   Left subscript = 2 * parent + 1
   Right subscript = 2 * parent + 2

If the child subscript is known, then:
Parent subscript = (child - 1) / 2

2, heap

• Heap is logically a complete binary tree
• The heap is physically stored in an array
• If the value of any node is greater than the value of the node in its subtree, it is called a large heap, or a large root heap, or a maximum heap
• Pile or small root, or vice versa
• The basic function of heap is to quickly find the most important value in the set

1. Method

Each time you join the team, you need to ensure that the current is a large root pile or a small root pile
Each time an element pops up, it is still a large root heap or a small root heap

public class TestDemo {
    public static void main(String[] args) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        // Every time you put an element, you must ensure that the current heap is a large heap or a small heap
        priorityQueue.offer(1);
        priorityQueue.offer(2);
        priorityQueue.offer(3);

        System.out.println(priorityQueue.peek()); // 1 - > small heap by default
    }
}

Operation - adjust to large root heap

Starting from the last subtree, each subtree is adjusted downward

public class TestHeap {
    public int[] elem;
    public int usedSize;

    public TestHeap() {
        this.elem = new int[10];
    }

    /**
     * Downward adjustment
     * @param parent Root node of each tree
     * @param len End position of each tree adjustment
     */
    public void shiftDown(int parent, int len) {
        int child = 2 * parent + 1;
        // Judge right child
        while(child < len) {
            if(child + 1 < len && this.elem[child] < this.elem[child + 1]) {
                child++; // child refers to the subscript with the largest value in the left and right children
            }
            if(this.elem[child] > this.elem[parent]) {
                int tmp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = tmp;
                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }

    public void createHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            this.elem[i] = array[i];
            usedSize++;
        }
        // Parent subscript = (child - 1) / 2
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            // adjustment
            shiftDown(parent, usedSize);
        }
    }
}

public class TestDemo {
    public static void main(String[] args) {
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        TestHeap testHeap = new TestHeap();
        testHeap.createHeap(array);
    }
}

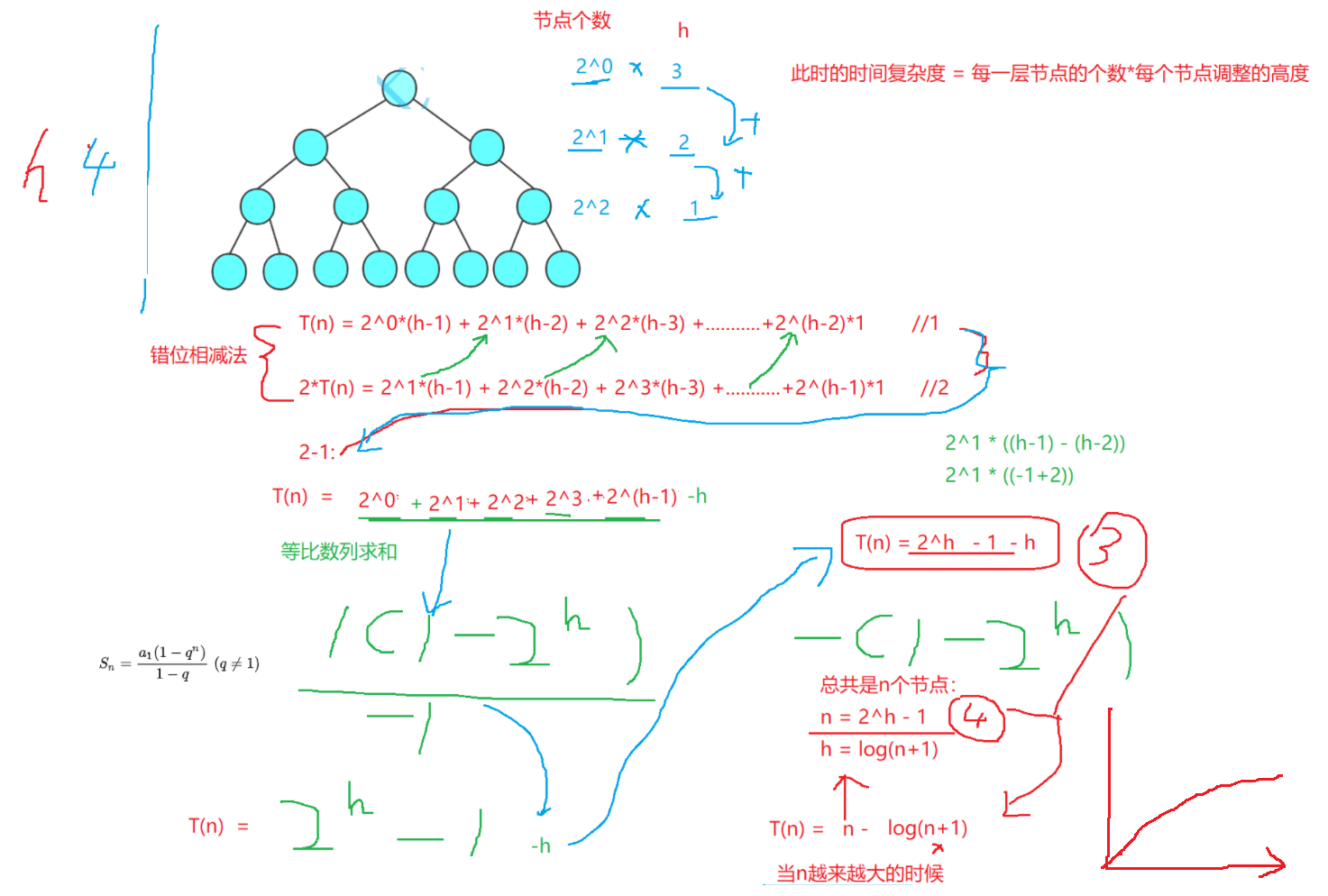
Time complexity analysis:
The worst case is the case shown in the figure. From the root to the leaf, the number of comparisons is the height of the complete binary tree
That is, the time complexity is O(log(n))

Queue

private void shiftUp(int child) {
        int parent = (child - 1) / 2;
        while(child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    // Upward adjustment
    public void offer(int val) {
        if(isFull()) { // Capacity expansion
            elem = Arrays.copyOf(elem, 2*elem.length);
        }
        this.elem[usedSize++] = val;
        shiftUp(usedSize - 1);
    }

    public boolean isFull() {
        return usedSize == this.elem.length;
    }

Out of queue

Every time you leave the queue, you should ensure that the maximum or minimum number is selected
1. Swap 0 subscript and last element
2. Adjust 0 subscript

public int pop() {
        if(isEmpty()) {
            throw new RuntimeException("Priority queue is empty");
        }
        // 1. Swap 0 subscript and last element
        int tmp = elem[0];
        elem[0] = elem[usedSize - 1];
        elem[usedSize - 1] = tmp;
        // 2. Adjust 0 subscript
        shiftDown(0, usedSize);
        return tmp;
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

Get team leader element

public int peek() {
        if(isEmpty()) {
            throw new RuntimeException("Priority queue is empty");
        }
        return elem[0];
    }

2. Other applications of heap

2.1 TopK problem

Find the top 3 largest elements:
1. Build the first three elements into a small root heap
2. The element at the top of the heap is the smallest of the current k elements
3. If the next X element is larger than the top of the heap element, the top of the heap element is removed to the end, the X element is inserted, and then the top of the heap element is adjusted to a small root heap again

Time complexity: O(n*logk)
Adjust the heap to the height of the heap logk

Summary:

• If the first k largest elements are required, a large root heap should be built, and the elements in the heap are the first k largest elements
• If the first k smallest elements are required, a small root heap should be built, and the elements in the heap are the first k smallest elements
  The heap top element is larger than the next one. Remove the heap top element and adjust it
• For the k-th element, build a small heap, and the top element is the k-th element
• For the k-th smallest element, build a large pile, and the top element is the k-th smallest element

-Find the first K smallest elements in the array

import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;

public class TopK {
    // n*logn
    public static int[] topK(int[] array, int k) {
        // 1. Create a large root heap with size K
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1; // Big root pile
            }
        });
        // 2. Traverse the elements in the array, and put the first K elements in the queue
        for (int i = 0; i < array.length; i++) {
            if(maxHeap.size() < k) {
                maxHeap.offer(array[i]);
            } else {
                // 3. Starting with the k+1 element, each element is compared with the top element
                int top = maxHeap.peek();
                if(top > array[i]) {
                    // 3.1. Pop up first
                    maxHeap.poll();
                    //3.2 post deposit
                    maxHeap.offer(array[i]);
                }
            }
        }
        // 4. Store the first K elements and return
        int[] ret = new int[k];
        for (int i = 0; i < k; i++) {
            ret[i] = maxHeap.poll();
        }
        return ret;
    }

    public static void main(String[] args) {
        int[] array = {18,21,8,10,34,12};
        int[] ret = topK(array, 3);
        System.out.println(Arrays.toString(ret));
    }
}

- LeetCode 373. Find and minimum K-pair numbers

373. Find and the smallest K-pair number

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        // Create a large root heap of size K
        PriorityQueue<List<Integer>> maxHeap = new PriorityQueue<>(k, new Comparator<List<Integer>>() {
            @Override
            public int compare(List<Integer> o1, List<Integer> o2) {
                return (o2.get(0) + o2.get(1)) - (o1.get(0) + o1.get(1)); // Big root pile
            }
        });
        // Add the K-group sequence and compare the top elements
        for (int i = 0; i < Math.min(nums1.length, k); i++) {
            for (int j = 0; j < Math.min(nums2.length, k); j++) {
                if(maxHeap.size() < k) {
                    List<Integer> list = new ArrayList<>();
                    list.add(nums1[i]);
                    list.add(nums2[j]);
                    maxHeap.offer(list);
                } else {
                    // Heap top element large poll
                    int top = maxHeap.peek().get(0) + maxHeap.peek().get(1);
                    if(top > nums1[i] + nums2[j]) {
                        maxHeap.poll();
                        List<Integer> list = new ArrayList<>();
                        list.add(nums1[i]);
                        list.add(nums2[j]);
                        maxHeap.offer(list);
                    }
                }
            }
        }
        // Storage k group sequence
        List<List<Integer>> ret = new ArrayList<>();
        for (int i = 0; i < k && !maxHeap.isEmpty(); i++) { // No k group null pointer exception
            ret.add(maxHeap.poll());
        }

        return ret;
    }
}

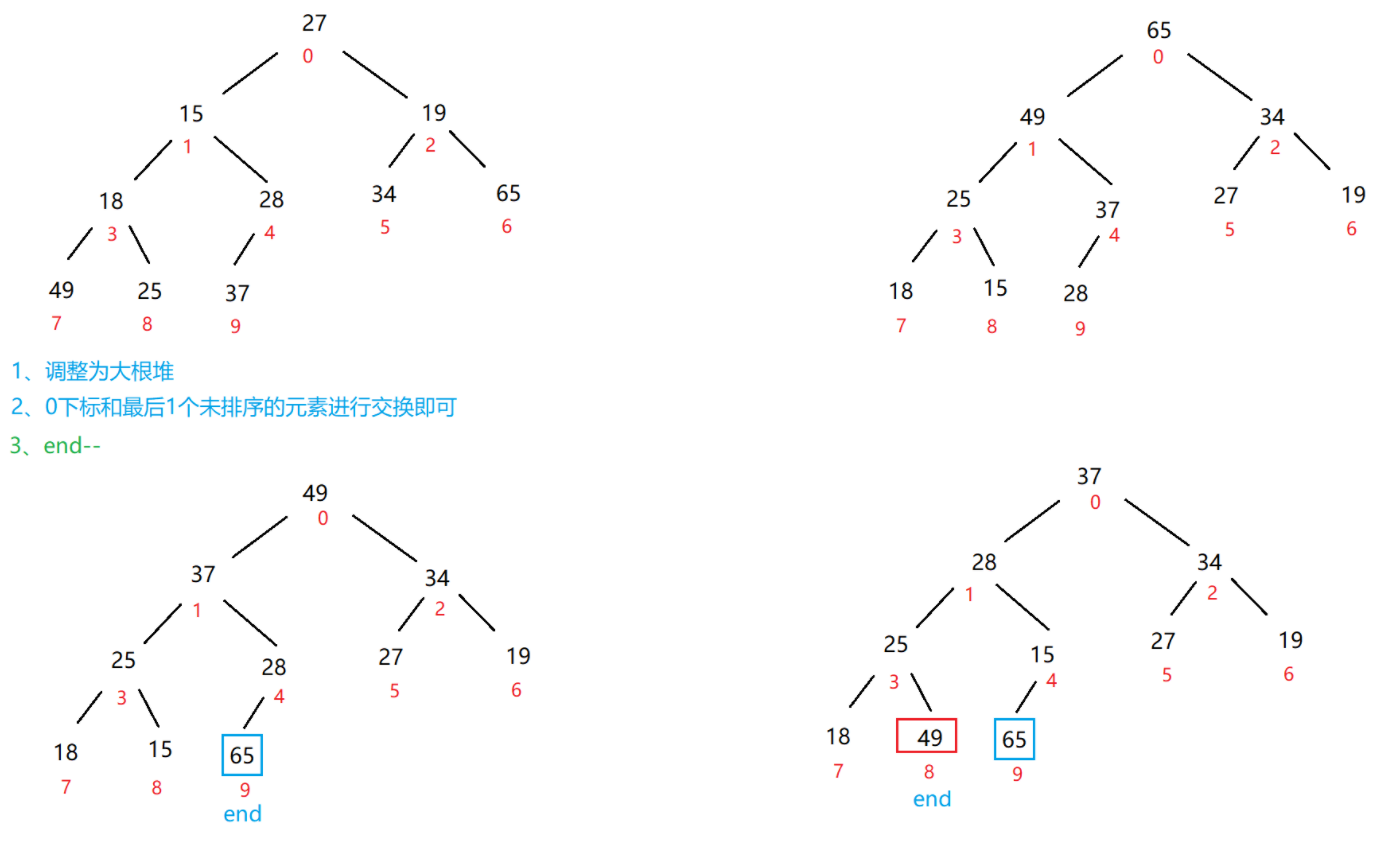
2.2 heap sorting

Sort a group of data from small to large. Build a large root heap or a small root heap?
It should be a small root heap, because instead of popping the top element of the heap every time, this array is sorted

	/**
     * Heap sort
     * 1,0 Subscripts are exchanged with the last unordered subscript
     * 2,end--
     */
    public void heapSort() {
        for (int end = usedSize - 1; end > 0; end--) {
            int tmp = elem[0];
            elem[0] = elem[end];
            elem[end] = tmp;
            shiftDown(0, end);
        }
    }

TestHeap.java

import java.util.Arrays;

public class TestHeap {
    public int[] elem;
    public int usedSize;

    public TestHeap() {
        this.elem = new int[10];
    }

    /**
     * Downward adjustment
     * @param parent Root node of each tree
     * @param len End position of each tree adjustment
     */
    public void shiftDown(int parent, int len) {
        int child = 2 * parent + 1;
        // Judge right child
        while(child < len) {
            if(child + 1 < len && this.elem[child] < this.elem[child + 1]) {
                child++; // child refers to the subscript with the largest value in the left and right children
            }
            if(this.elem[child] > this.elem[parent]) {
                int tmp = this.elem[child];
                this.elem[child] = this.elem[parent];
                this.elem[parent] = tmp;
                parent = child;
                child = 2 * parent + 1;
            } else {
                break;
            }
        }
    }

    public void createHeap(int[] array) {
        for (int i = 0; i < array.length; i++) {
            this.elem[i] = array[i];
            usedSize++;
        }
        // Parent subscript = (child - 1) / 2
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            // adjustment
            shiftDown(parent, usedSize);
        }
    }


    private void shiftUp(int child) {
        int parent = (child - 1) / 2;
        while(child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }

    // Queue up adjustment
    public void offer(int val) {
        if(isFull()) { // Capacity expansion
            elem = Arrays.copyOf(elem, 2*elem.length);
        }
        this.elem[usedSize++] = val;
        shiftUp(usedSize - 1);
    }

    public boolean isFull() {
        return usedSize == this.elem.length;
    }


    // Out of queue
    public int pop() {
        if(isEmpty()) {
            throw new RuntimeException("Priority queue is empty");
        }
        // 1. Swap 0 subscript and last element
        int tmp = elem[0];
        elem[0] = elem[usedSize - 1];
        elem[usedSize - 1] = tmp;
        // 2. Adjust 0 subscript
        shiftDown(0, usedSize);
        return tmp;
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

    public int peek() {
        if(isEmpty()) {
            throw new RuntimeException("Priority queue is empty");
        }
        return elem[0];
    }


    /**
     * Heap sort
     * 1,0 Subscripts are exchanged with the last unordered subscript
     * 2,end--
     */
    public void heapSort() {
        for (int end = usedSize - 1; end > 0; end--) {
            int tmp = elem[0];
            elem[0] = elem[end];
            elem[end] = tmp;
            shiftDown(0, end);
        }
    }
}

3, Comparison of java objects

1. Question raised

The priority queue has a requirement when inserting elements: the inserted elements cannot be null or the elements must be able to be compared. For simplicity, we only inserted Integer type. Can we insert custom type objects in the priority queue?

class Card {
    public int rank; // numerical value
    public String suit; // Decor

    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }
}

public class TestPriorityQueue {
    public static void TestPriorityQueue() {
        PriorityQueue<Card> p = new PriorityQueue<>();
        p.offer(new Card(1, "♠"));
        p.offer(new Card(2, "♠"));
    }
    public static void main(String[] args) {
        TestPriorityQueue();
    }
}

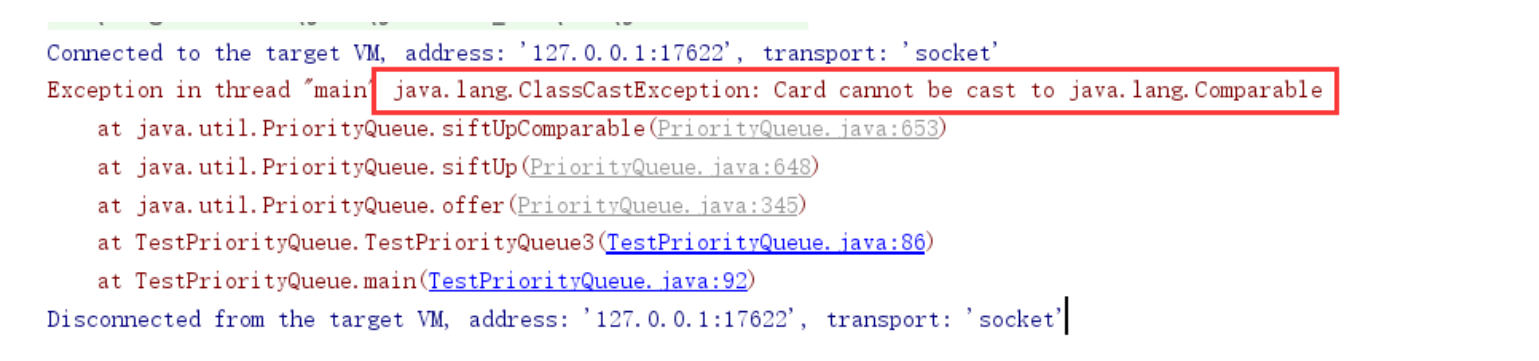
The bottom layer of the priority queue uses the heap. When inserting elements into the heap, in order to meet the nature of the heap, the elements must be compared. At this time, the Card has no way to compare directly, so an exception is thrown

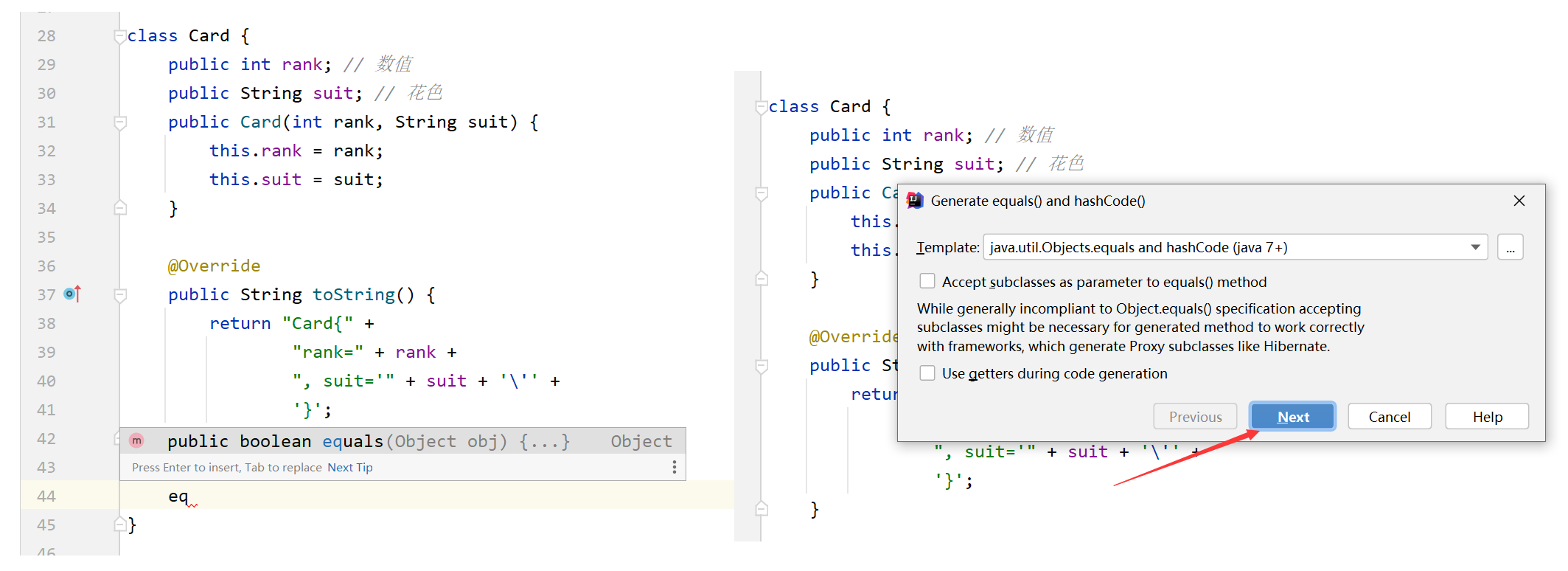
2. Override equal of base class

• If the equals method is not overridden, object is called by default
  

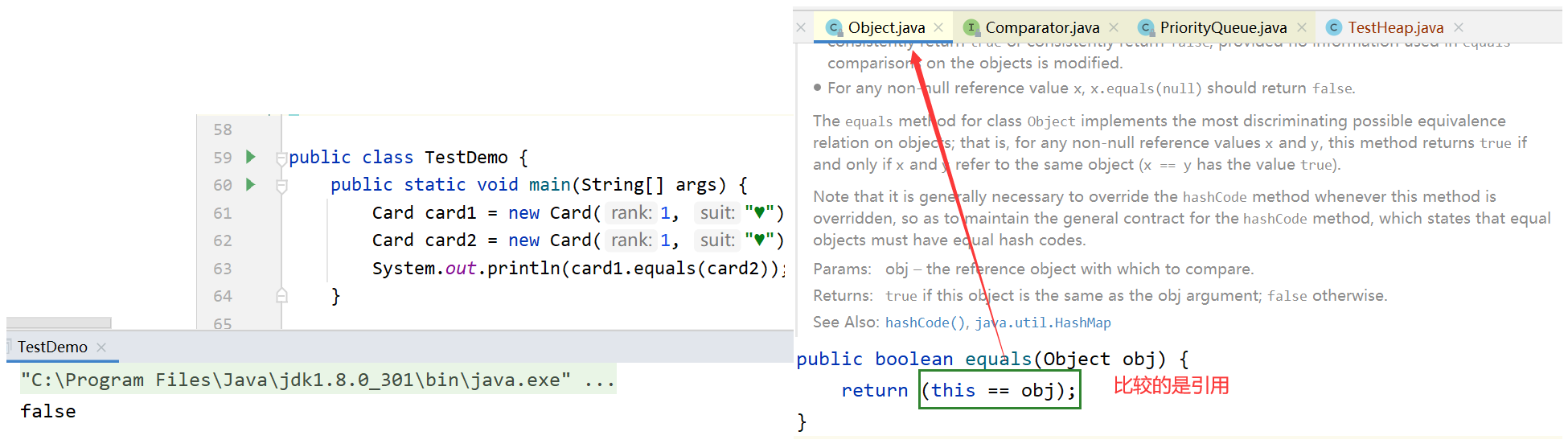
• Override the equals method:

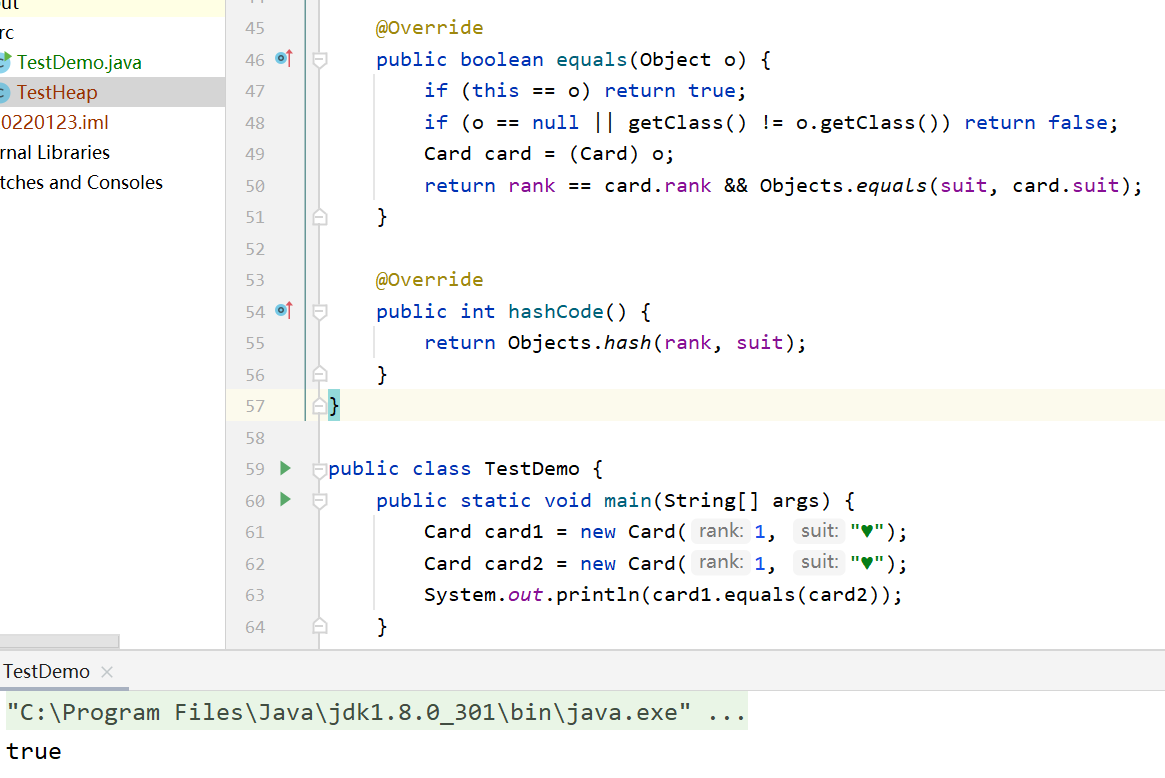
public class Card {
    public int rank; // numerical value
    public String suit; // Decor

    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }

    @Override
    public boolean equals(Object o) {
        // Compare yourself with yourself
        if (this == o) return true;
        
        // o if it is a null object, or o is not a subclass of Card
        // getClass() != o.getClass() compares the same type
        if (o == null || getClass() != o.getClass()) return false;

        // Strong conversion to Card type
        Card c = (Card) o;
        
        // Compare whether the value and color are the same
        return rank == card.rank && Objects.equals(suit, card.suit);
    }

	@Override
    public int hashCode() {
        return Objects.hash(rank, suit);
    }
}

Basic types can be compared directly, but it is better for reference types to call their equal method

Note: the general routine of overriding equals is demonstrated above

1. Returns true if it points to the same object
2. If the passed in is null, false is returned
3. If the object type passed in is not Card, false is returned
4. Complete the comparison according to the realization goal of the class. For example, as long as the color and value are the same, it is considered to be the same card
5. Note that equals is also required to call the comparison of other reference types, such as the comparison of suit here
   Although the method of overriding the base class equal can be compared, the defect is that equal can only be compared according to equality, not greater than or less than.

3. Comparison of interface classes based on Comparble

public interface Comparable<E> {
	// Return value:
	// < 0: indicates that the object pointed to by this is less than the object pointed to by o
	// ==0: indicates that the object pointed to by this is equal to the object pointed to by o
	// >0: indicates that the object pointed to by this is equal to the object pointed to by o
	int compareTo(E o);
}

For user-defined types, if you want to compare by size and mode: when defining a class, you can implement the Comparble interface, and then override the compareTo method in the class

class Card implements Comparable<Card>{
    public int rank; // numerical value
    public String suit; // Decor
    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }

    @Override
    public int compareTo(Card o) {
        return this.rank - o.rank;
    }

    @Override
    public String toString() {
        return "Card{" +
                "rank=" + rank +
                ", suit='" + suit + '\'' +
                '}';
    }
}

public class TestDemo {
    public static void main(String[] args) {
        // The default is small root heap
        PriorityQueue<Card> priorityQueue = new PriorityQueue<>();
        priorityQueue.offer(new Card(1, "♥")); // Directly put the 0 subscript of the underlying queue array
        priorityQueue.offer(new Card(2, "♥"));
        System.out.println(priorityQueue); 
        // Result: [Card{rank=1, suit = ' ♥'},  Card{rank=2, suit=' ♥'}]

        // priorityQueue.offer(null); // err ->NullPointerException
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Card card1 = new Card(2, "♥");
        Card card2 = new Card(1, "♦");

        System.out.println(card1.compareTo(card2)); // 1 - > first card big
    }
}

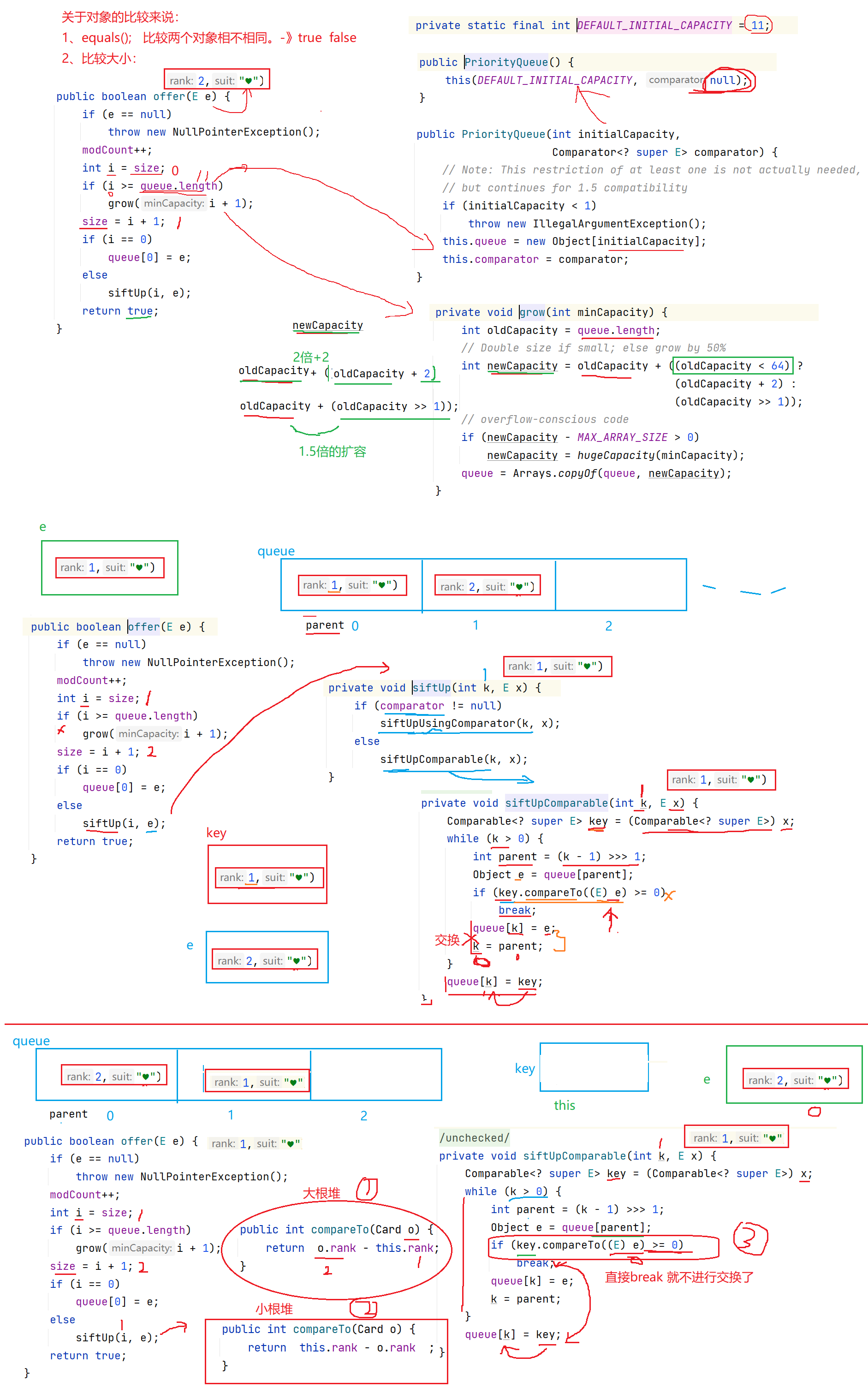
Disadvantages: the class is too intrusive. Once it is written and compared according to which rule, it cannot be easily modified

4. Comparator based comparison

class Card {
    public int rank; // numerical value
    public String suit; // Decor
    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }
}

class RankComparator implements Comparator<Card> {
    @Override
    public int compare(Card o1, Card o2) {
        return o1.rank - o2.rank;
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Card card1 = new Card(1, "♥");
        Card card2 = new Card(2, "♦");

        RankComparator rankComparator = new RankComparator();
        int ret = rankComparator.compare(card1, card2);
        System.out.println(ret); // -1
    }
}

Comparison queue:

class Card {
    public int rank; // numerical value
    public String suit; // Decor
    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }

    @Override
    public String toString() {
        return "Card{" +
                "rank=" + rank +
                ", suit='" + suit + '\'' +
                '}';
    }
}

class RankComparator implements Comparator<Card> {
    @Override
    public int compare(Card o1, Card o2) {
        return o1.rank - o2.rank;
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Card card1 = new Card(1, "♥");
        Card card2 = new Card(2, "♦");

        RankComparator rankComparator = new RankComparator();

        PriorityQueue<Card> priorityQueue = new PriorityQueue<>(rankComparator);
        priorityQueue.offer(card1);
        priorityQueue.offer(card2);
        System.out.println(priorityQueue);
        // [Card{rank=1, suit='♥'}, Card{rank=2, suit='♦'}]
    }
}

Anonymous inner class:

class Card {
    public int rank; // numerical value
    public String suit; // Decor
    public Card(int rank, String suit) {
        this.rank = rank;
        this.suit = suit;
    }

    @Override
    public String toString() {
        return "Card{" +
                "rank=" + rank +
                ", suit='" + suit + '\'' +
                '}';
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Card card1 = new Card(2, "♥");
        Card card2 = new Card(1, "♦");
        // 1,
        PriorityQueue<Card> priorityQueue =  new PriorityQueue<>(new Comparator<Card>() {
            @Override
            public int compare(Card o1, Card o2) {
                return o1.rank - o2.rank;
            }
        });

        // 2. lambda expression - > very poor readability
        // PriorityQueue<Card> priorityQueue = new PriorityQueue<>((x, y) -> {return x.rank - y.rank;});

        priorityQueue.offer(card1);
        priorityQueue.offer(card2);
        System.out.println(priorityQueue); // [Card{rank=1, suit='♦'}, Card{rank=2, suit='♥'}]
    }
}

5. Comparison of three methods

Override method	explain
Object.equals	Because all classes inherit from Object, you can override them directly, but you can only compare equality with
no
Comparable.compareTo	The interface needs to be implemented manually, which is highly invasive, but once implemented, this class is used in order every time, which belongs to
Internal sequence
Comparator.compare	It is necessary to implement a comparator object, which is less intrusive to the comparison class, but intrusive to the algorithm code
strong