Reference:

https://blog.csdn.net/lyhkmm/article/details/78920769

https://blog.csdn.net/u012681635/article/details/80453664

https://www.zhihu.com/people/dong-hua-xue-bian-cheng

 

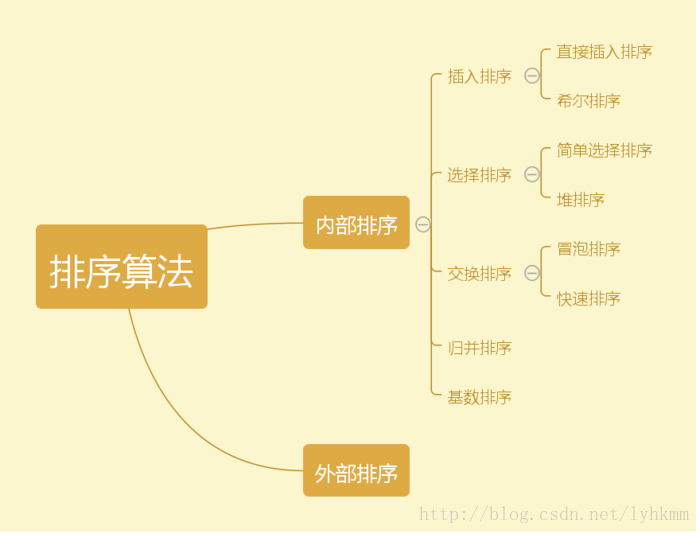
Sorting algorithm:

1. Simple sorting: bubble, select, insert

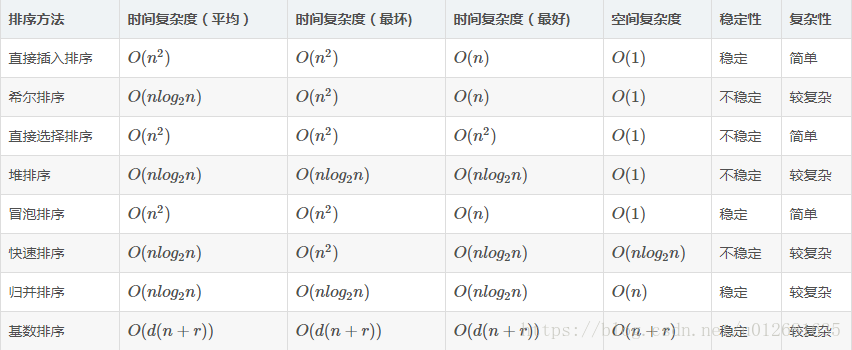
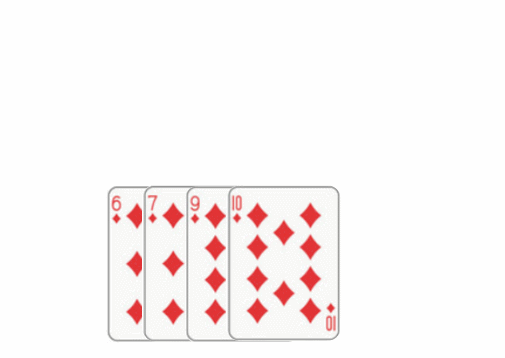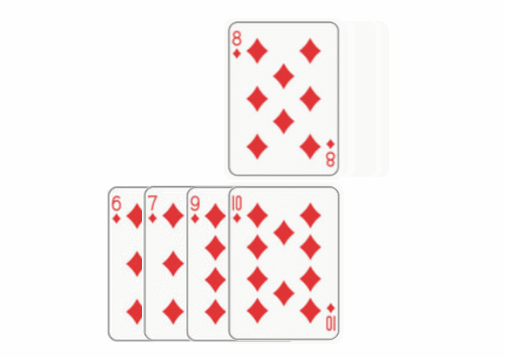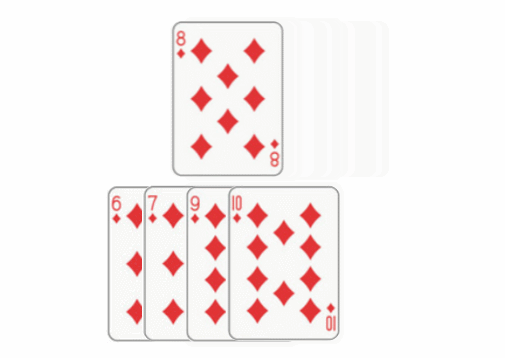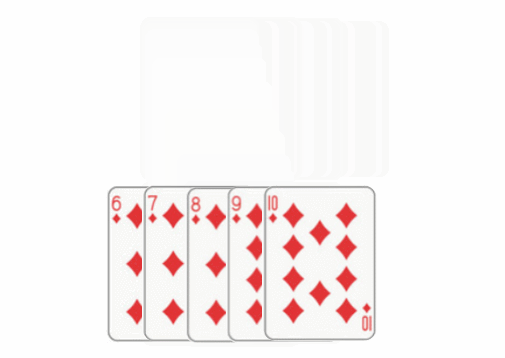
1.1: bubble sorting: compare two by two. If the front is greater than the rear, change the position until the largest bubble reaches the top. Exchange O(N^2), compare O(N^2)

　　　　　　

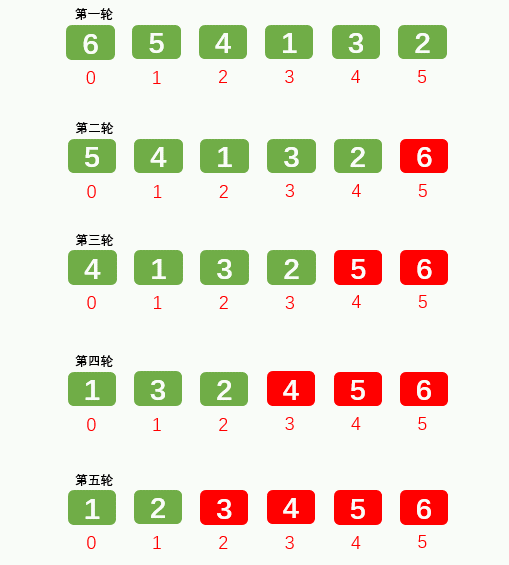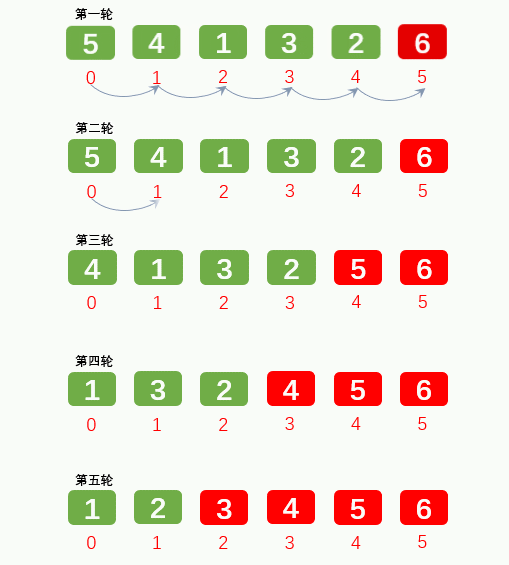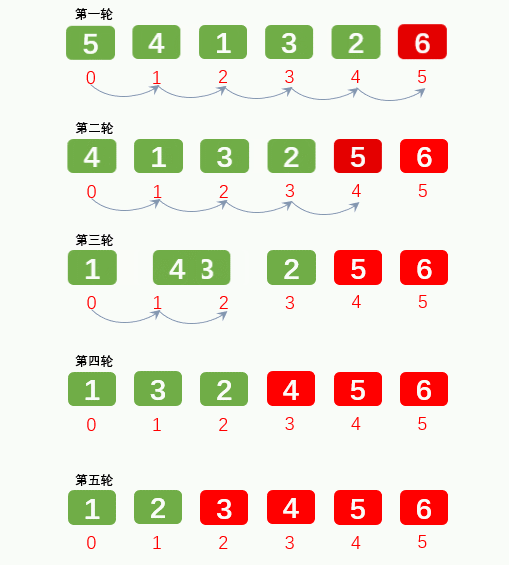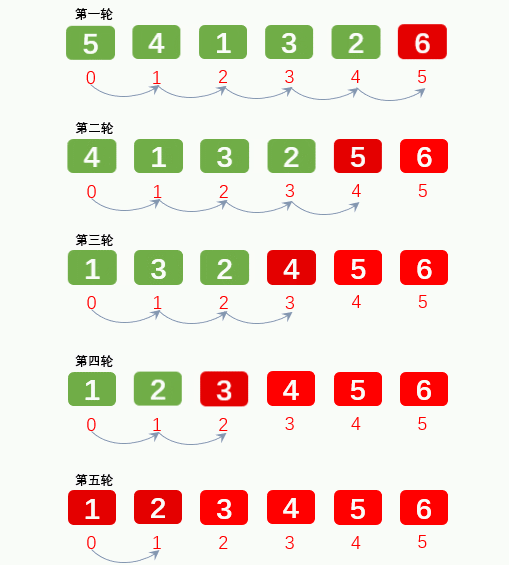
1.2: Select Sorting: take out the minimum / maximum position and exchange with the first / last position. Exchange O(N), compare O(N^2)

　　　　　　

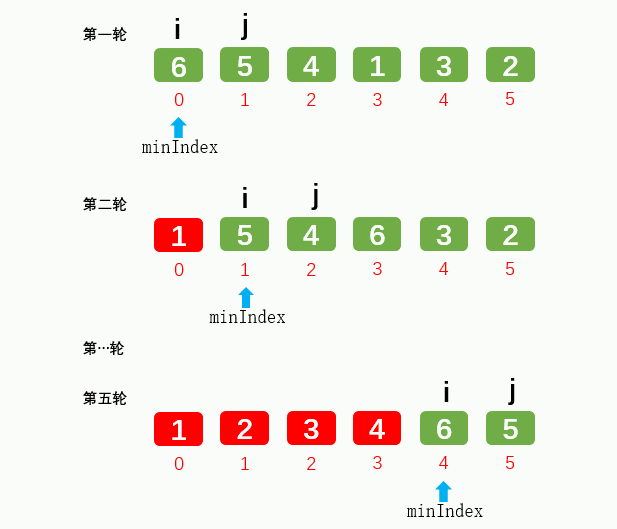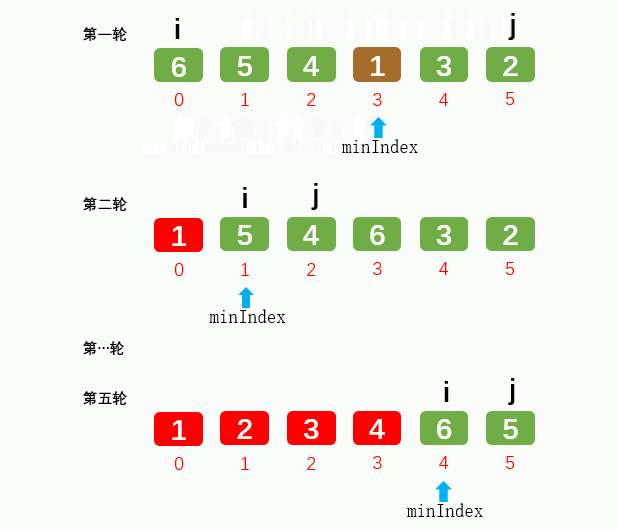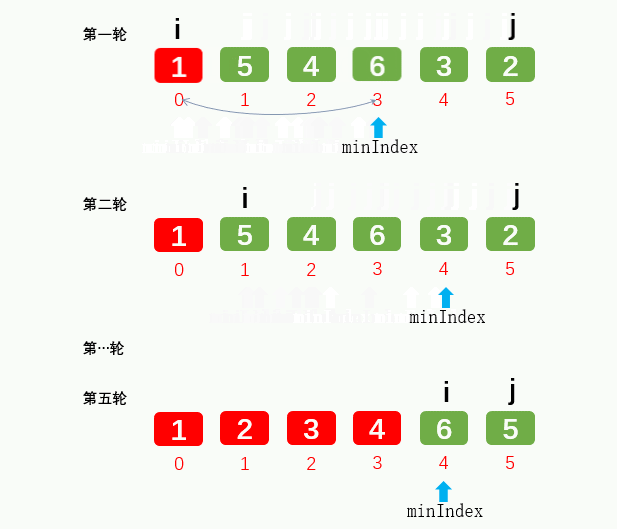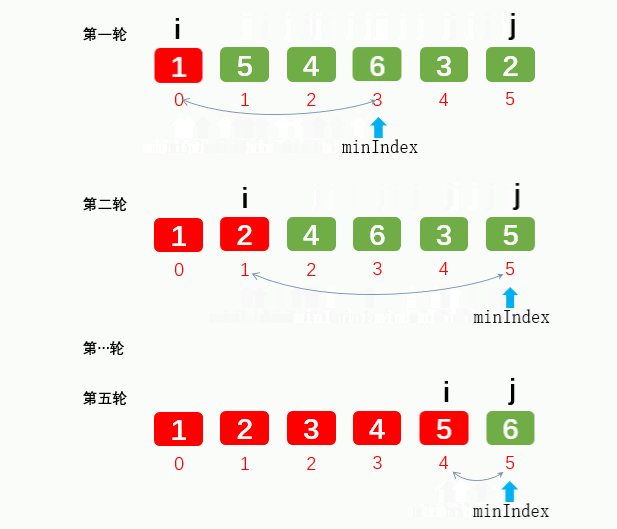
1.3: insertion sort: the core idea is local order. Take out the latter one to be compared, and then compare to judge whether to move (not exchange). Due to the local order, if there is no need to move, the subsequent elements do not need to be compared, and the extracted elements are assigned to the position where the comparison is stopped. Efficiency is the highest in simple sorting. Swapping O(N) and comparing O(N^2) look the same as selection sorting, but they are actually half less than bubbling and selection, and the movement is more efficient than swapping

　　　　　　

 

2. Advanced sorting: Hill, fast, merge, technology, cardinality, heap, bucket

2.1: Hill sort: improved insertion sort, with higher efficiency.

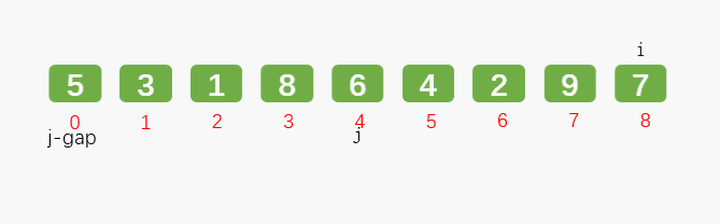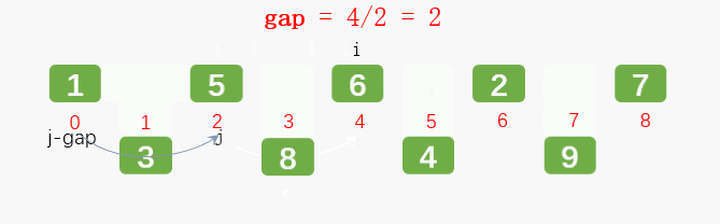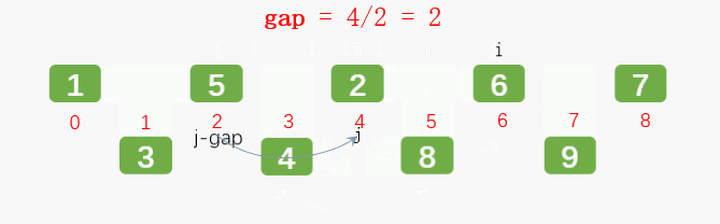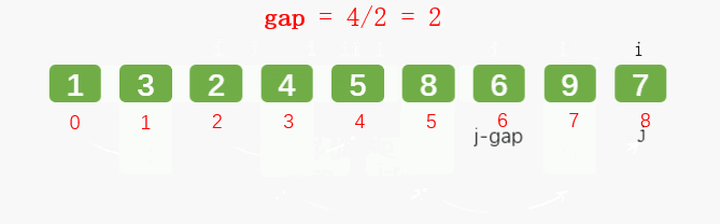
Main idea: set the interval and reorder to make the numbers closer to their correct position.

Incremental problem: how to choose the appropriate interval?

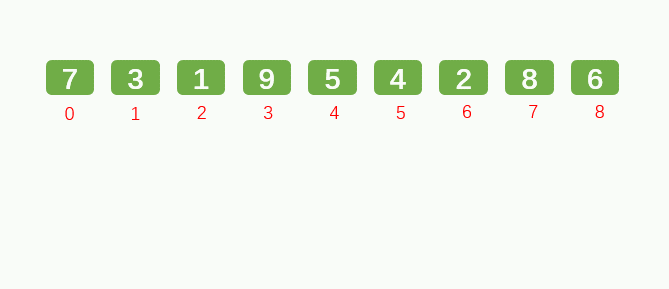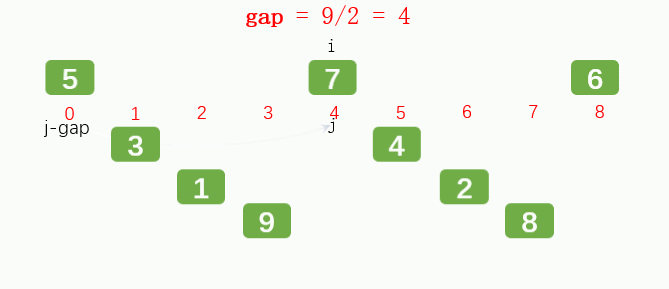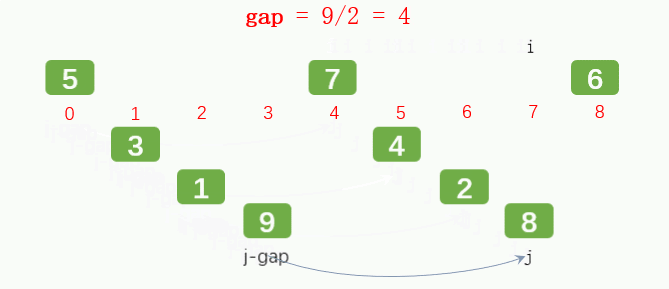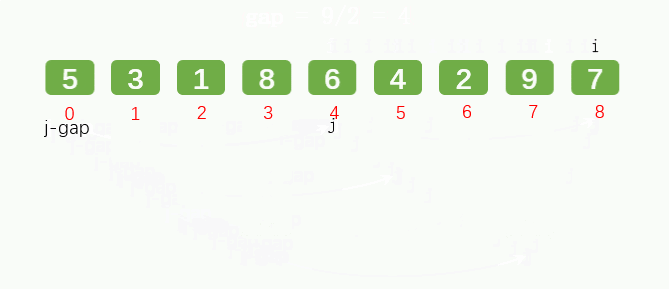
Hill's manuscript suggests that the initial interval is N (number of numbers) / 2, which does not need to be calculated to find an appropriate increment before sorting; And Hibbard, Sedgewick, etc.

Hill's efficiency is closely related to the choice of increment, but it is difficult to infer because some increments cannot be proved. But in the worst case, the original increment can also reach O(N^2), so it is usually smaller than it

First gap:

　　　　　　

 

Second gap:

 　　　　　　

 

Third gap:

 　　　　　　

 

 

2.2: quick sort: Generally speaking, it is the most efficient sort and can be regarded as advanced bubble

In a loop (recursion), the correct position of the element is found, and no movement is required after the element

Main idea: divide and conquer (D & C): decompose the original problem into several small-scale subproblems similar to the original problem, solve these subproblems recursively, and then combine the solutions of these subproblems to establish the solution of the original problem.

Take an element, place it on the right and less on the left, and recurse the function

Main operations: select pivot principal component. Generally take the median of head, middle and tail

Efficiency: it mainly depends on the choice of hub. In the worst case, the hub is the rightmost or leftmost, and its efficiency is equivalent to bubbling. The average efficiency is O(N*logN)

The pivot shown in the figure takes the last value, and the idea is basically similar to the subordinate code below.

　　　　　　　　

 

 

 function ArrayList() {
      //attribute
      this.array = []
      //method
      //Data insertion
      ArrayList.prototype.insert = function (item) {
        this.array.push(item)
      }

      ArrayList.prototype.toString = function () {
        return this.array.join(' ')
      }

      //Define a function that exchanges variables
      ArrayList.prototype.swap = function (m, n) {
        let temp = this.array[m]
        this.array[m] = this.array[n]
        this.array[n] = temp
      }

      //Bubbling
      ArrayList.prototype.bubbleSort = function () {
        for (let n = 0; n < this.array.length; n++) {
          for (let i = 0; i < this.array.length - n; i++) {
            if (this.array[i] > this.array[i + 1]) {
              this.swap(i, i + 1)
            }
          }
        }
      }
      //choice
      ArrayList.prototype.selectionSort = function () {
        let length = this.array.length
        let index = null
        for (let n = 0; n < length; n++) {
          index = 0
          for (let i = 0; i < length - n - 1; i++) {
            if (this.array[index] < this.array[i + 1]) {
              index = i + 1
            }
          }
          //If there is a value greater than him, exchange it with the last bit, otherwise it will not operate
          if (index != 0) {
            this.swap(index, length - 1 - n)
          }
        }
      }
      //insert
      ArrayList.prototype.insertionSort = function () {
        if (this.array.length > 1) {
          for (let i = 1; i < this.array.length; i++) {
            let temp = this.array[i]
            //Here greater than-1 So that when the inserted element is the last, the last else Replication of
            for (let j = i - 1; j >= -1; j--) {
              if (temp < this.array[j]) {
                this.array[j + 1] = this.array[j]
              } else {
                this.array[j + 1] = temp
                break
              }
            }
          }
        }

      }
      //Hill
      ArrayList.prototype.shellSort = function () {
        let gap = Math.floor(this.array.length / 2)
        while (gap >= 1) {
          //The following is actually the insertion sort. The interval of the previous value has changed from 1 to gap
          for (let i = gap; i < this.array.length; i++) {
            let temp = this.array[i]
            for (let j = i - gap; j >= -gap; j = j - gap) {
              if (temp < this.array[j]) {
                this.array[j + gap] = this.array[j]
              } else {
                this.array[j + gap] = temp
                break
              }
            }
          }
          gap = Math.floor(gap / 2)
        }

      }
      //fast
      //Hub selection: the median of head, middle and tail. This is recursive, so the left and right values should be passed in
      ArrayList.prototype.medium = function (left, right) {
        let center = Math.floor((left + right) / 2)
        //Simple sort exchange first
        //Sequential execution
        if (this.array[right] < this.array[left]) {
          this.swap(right, left)
        }
        if (this.array[center] < this.array[left]) {
          this.swap(center, left)
        }
        if (this.array[center] > this.array[right]) {
          this.swap(center, right)
        }
        //  Put the middle value in the second position, or the penultimate position
        //The purpose is to place all undecided values on the right or left for the next operation
        this.swap(left + 1, center)
        return this.array[left + 1]
      }

      ArrayList.prototype.quickSort = function () {
        this.quick(0, this.array.length - 1)
      }

      ArrayList.prototype.quick = function (left, right) {
        //Exit recursion when out of bounds
        if (left >= right) {
          return
        }
        let pivot = this.medium(left, right)

        //Record the position of the current left and right values
        let low = left + 1
        let high = right
        //exchange
        while (low < high) {
          while (this.array[low] <= pivot) {
            low++
          }
          while (this.array[high] > pivot) {
            high--
          }
          //We have to judge first low Is the value less than high,Or you'll cross the line
          if (low < high) {
            this.swap(low, high)
          }
        }

        //At the end of the cycle, the data are correctly placed on the left and right of the hub, and the hub is transposed
        this.swap(left + 1, low - 1)

        //Recursion, divide and conquer, and then process the left and right values
        this.quick(left, low - 1)
        this.quick(low, right)

      }
    }