1, Title Requirements
2, Huffman coding
N weights are given as n weights leaf node , construct a binary tree. If the weighted path length of the tree reaches the minimum, such a binary tree is called the optimal binary tree, also known as Huffman tree. Huffman tree is the tree with the shortest weighted path length, and the node with larger weight is closer to the root.
For how to generate Huffman tree, see https://blog.csdn.net/qq_29519041/article/details/81428934
3, Design ideas
If we usually use c language to do this problem, we must think of pointers at the first time, which are used to point to its left and right subtrees and parent nodes. In the assembly, there is no pointer operation. Therefore, I think of a new idea, which is similar to simulating a tree. There are one-dimensional arrays in assembly language, and one-dimensional arrays are enough to solve this problem.
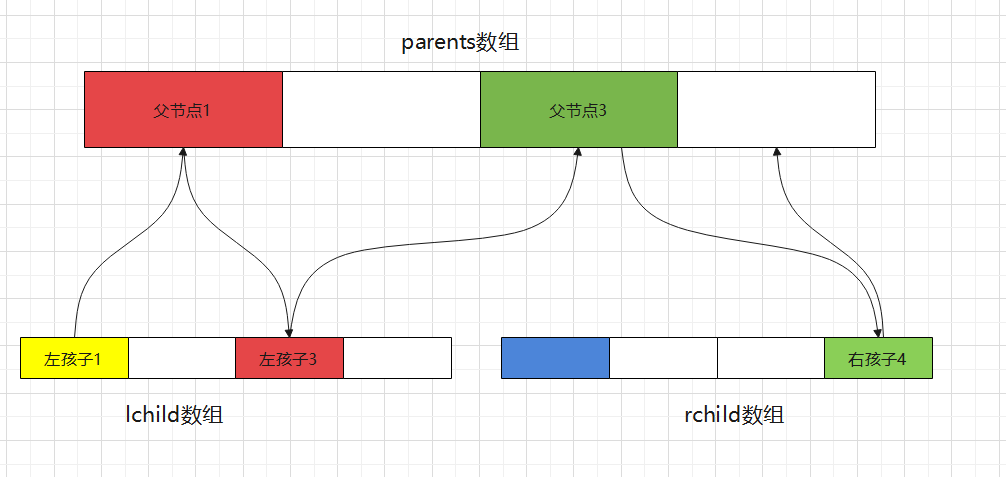
1. First, we need three arrays, the parents array, which are stored in the process of generating the Huffman tree. All parent nodes and lchird array are stored in the process of generating the Huffman tree. All nodes that become left children are stored in the same way as rchird.
2. Sort the initial frequency (the frequency is a decimal, but I use an integer, as long as it can express the size relationship between frequencies) from small to large (I use bubble sorting here because it is simple to implement). In particular, adding can directly find the minimum two frequencies without sorting, of course
3. Put the rules of the smallest two frequencies, small left and large right, into the left child array and right child array, and put their sum into the father array. From this, we can see that the position of the father node in the array is the same as that of the left child and right child. That is, they can find their father node directly through their own subscript. Then delete the smallest two and reinsert them into the frequency table.
4. Repeat 2 and 3 until there is only one root node in the frequency table.
5. Similar to the figure below, first find the child array in which the leaf node is required, and add the following figure. The yellow leaf node is in the left child array first, so add a 0 to its code first, and then find out who the father node is with the same subscript as his subscript. From the figure, you can see which child array the red belongs to. If you find it here, We should start from the place where the child array subscript is 1 (the array subscript starts from 0), because the left child and right child that are the same as or smaller than the father subscript must not be itself.
6. Here we see that the red parent node belongs to the left child 3 again. Add another 0 to all codes and repeat 5 and 6 until the found parent node is the last of the parent array, that is, the root node, and the search ends.
7. Reverse the encoding just now.
4, Assembly code
include vcIO.inc
.data
Huffman_code dword 20 dup(?)
parents dword 20 dup(?)
rchird dword 20 dup(?)
lchird dword 20 dup(?)
r_point dword ?
l_point dword ?
char byte 'abcdef'
number dword 2,5,3,6,8,1
length_number dword ?
l_num dword 0 ;Number of left subtree arrays
r_num dword 0 ;Number of right subtree arrays
p_num dword 0 ;Number of parent node arrays
now_num dword ?
len dword lengthof number
number1 dword 20 dup(?)
info_print byte '%c The Huffman code is:',0,0
type_print byte '%d',0,0
speace_print byte ' ',10,0
temp dword ?
now_char dword ?
.code
main proc
mov length_number,lengthof number
mov ecx,lengthof number ;Make a copy number Copy of
mov esi ,0
loop2:
mov eax,number[esi*4]
mov number1[esi*4],eax
inc esi
loop loop2
mov ecx,lengthof number
loop_sort: ;The minimum two numbers of the loop
call sort
call add_array
dec ecx
cmp ecx,1
ja loop_sort
mov ecx ,len
mov esi,0
loop_find:
mov eax,number1[esi*4]
mov now_num,eax ;Find the Huffman code of each character, zero on the left and one on the right
mov bl,char[esi]
mov now_char,ebx
call find_code
inc esi
loop loop_find
ret
main endp
sort proc ;sort
push ecx
push eax
push ebx
push edx
mov ecx ,0
mov eax ,0
mov ebx,1
out_loop: ;Bubble sorting
cmp ecx,length_number
ja out1
inter_loop:
cmp ebx,length_number
je out2
mov edx,number[ebx*4]
cmp number[eax*4],edx
jl not_exchange ;If the front is bigger than the back, exchange
xchg number[eax*4],edx
xchg number[ebx*4],edx
not_exchange:
inc eax
inc ebx
jmp inter_loop
out2:
mov eax ,0
mov ebx ,1
inc ecx
jmp out_loop
out1:
pop edx
pop ebx
pop eax
pop ecx
ret
sort endp
add_array proc ;Add those belonging to the parent node to the parent node array and those belonging to the child node to the child node array
push ecx
push eax
push ebx
push edx
mov ecx,l_num
mov eax,r_num
mov edx ,number[4]
mov ebx,number[0]
mov rchird[ecx*4], edx
mov lchird[eax*4], ebx
add edx,ebx
mov ecx ,p_num
mov parents[ecx*4],edx
inc l_num
inc r_num ;Add one to all three arrays
inc p_num
mov ecx,0 ;Merge original array
mov ebx,1
loop1:
cmp ebx,length_number
ja out3
mov eax,number[ebx*4]
mov number[ecx*4],eax
inc ecx
inc ebx
jmp loop1
out3:
mov number[0],edx
dec length_number
pop edx
pop ebx
pop eax
pop ecx
ret
add_array endp
find_code proc
push ecx
push eax
push ebx
push esi
push edx
push now_num
mov ebx,0
mov ecx,p_num
mov temp,ecx
mov esi,0
loop_code:
mov eax,now_num
loop_r:
cmp rchird[esi*4] ,eax
je nextr
inc esi
cmp esi,ecx
jne loop_r
mov esi,0
loop_l:
cmp lchird[esi*4] ,eax
je nextl
inc esi
cmp esi,ecx
jne loop_l
nextr:
mov Huffman_code[ebx*4],1
jmp find_p
nextl:
mov Huffman_code[ebx*4],0
find_p:
inc ebx
mov edx,parents[esi*4]
mov now_num,edx
inc esi
cmp esi,temp
jb loop_code
pop now_num
pushad
invoke printf ,offset info_print,now_char
popad
mov ecx,ebx
dec ebx
mov esi ,ebx
loop_print:
pushad
invoke printf ,offset type_print,Huffman_code[esi*4]
popad
dec esi
loop loop_print
pushad
invoke printf ,offset speace_print
popad
pop edx
pop esi
pop ebx
pop eax
pop ecx
ret
find_code endp
end main
5, Operation results
Input:
char byte 'abcdef'
number dword 2,5,3,6,8,1
Output:
The Huffman code of a is 0111
The Huffman code of b is: 00
The Huffman code of c is 011
The Huffman code of d is 01
The Huffman code of e is: 11
The Huffman code of f is 0110
6, Summary
When encountering problems, there are two ways: one is to overcome them, and the other is to bypass the pointer in c. It is very simple to solve this problem, but in assembly, we should think of using simulation to construct a tree to solve it. Sometimes, it is a good thing to change another way of thinking.