1, Experimental purpose
(1) According to the grammar specification of PL/0 language, it is required to write the syntax analysis program of PL/0 language.
(2) By designing, compiling and debugging a typical bottom-up grammar analysis program, we can realize the grammar check and structure analysis of the word sequence provided by the grammar analysis program, and further master the common grammar analysis methods.
(3) Choose the most representative grammar analysis methods, operator first analysis and LR analysis; Or investigate the function and working principle of YACC, the automatic generation tool of parser, and use YACC to generate a bottom-up parser.
2, Experimental content
(1) The PL/0 language grammar has been given to construct the parser of the expression part.
BNF of the analysis object arithmetic expression is defined as follows:
< expression >: = [+ | -] < item > {< addition operator > < item >}
< item >: = < factor > {< mu lt iplication operator > < factor >}
< factor >: = < identifier > | < unsigned integer > | '(' < expression > ')
< addition operator >: =+|-
< mu lt iplication operator >: =*|/
Syntax rules of the Bacos normal form (BNF):
The word ("word") in double quotation marks represents the characters themselves. And double_quote is used to represent double quotation marks.
The words outside the double quotation marks (possibly underlined) represent the grammatical part.
The included in angle brackets (< >) is required.
The contained in square brackets ([]) are optional.
Braces ({}) contain items that can be repeated 0 to countless times.
The vertical bar (|) means to choose one item on the left and right sides, which is equivalent to "OR".
:: = is defined as.
(2) Input according to the results of lexical analysis in Experiment 1. For example, for PL/0 expression, (a+15) * b uses the following form as input:
(lparen,( )
(ident, a)
(plus, + )
(number, 15)
(rparen,) )
(times, * )
(ident, b )
Output:
For expressions with correct syntax, the output is "Yes,it is correct."
For expressions with syntax errors, the output is "No,it is wrong."
3, Design idea and experimental steps
(1) Design idea
Operator priority analysis was used in this experiment. Operator priority analysis is a kind of priority relationship defined between operators. With the help of this priority relationship, we can find and regulate the string.
For grammar G:
< expression >: = [+ | -] < item > {< addition operator > < item >}
< item >: = < factor > {< mu lt iplication operator > < factor >}
< factor >: = < identifier > | < unsigned integer > | '(' < expression > ')
< addition operator >: =+|-
< mu lt iplication operator >: =*|/
< relational operator >: = | #| < = | >=
It can be rewritten as follows:
S' - > < expression >
< expression > - > < item >
< expression > - > < expression > + < item >
< expression > - > < expression > - < item >
< item > - > < factor >
< item > - > < item > * < factor >
< item > - > < item > / < factor >
< factor > - > (< expression >)
< factor > - > < identifier >
< factor > - > < unsigned integer >
Definition of operator grammar:
for A grammar, if the right part of any production does not contain two consecutive and parallel non terminators, such as A grammar g, if there is no production in G in the form of A →... BC... In which B and C are non terminators, then G is called operator grammar.
The priority relationship is defined as follows:
The priority of a is less than that of b
(1) A < b: if and only if the production of tangible such as P →... aR... In grammar G and R ⇒ + b... Or R ⇒ + Qb
The priority of a is equal to that of b
(2) a=b: if and only if the production of tangible forms such as P →... ab... Or P →... aQb... In grammar G
a has priority over b
(3) a > b: if and only if the production of tangible such as P →... Rb... In grammar G, and R ⇒ +... a or R ⇒ +... aR
If any terminator pair (a, b) in an operator grammar g satisfies at most one of the following three relationships: a < B, a = B, a > b, G is said to be an operator precedence grammar.
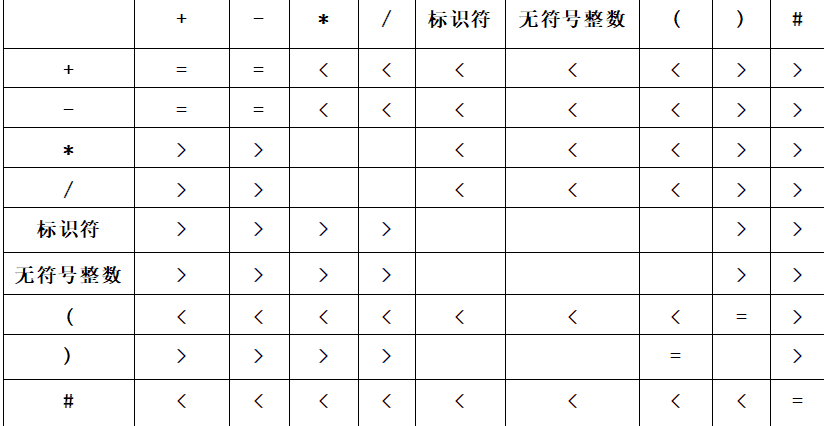
Construct the precedence relation table from the operator precedence grammar G:
Check each candidate of each production formula of G to find out all terminator pairs satisfying a=b. in order to find out all terminator pairs satisfying the relationship < and >, it is necessary to construct two sets FIRSTVT § and LASTVT § for each non terminator P of G.
Define and construct two sets of FIRSTVT and LASTVT
FIRSTVT § = {a|P ⇒ + a... Or P ⇒ + Qa...}
LASTVT § = {a|P ⇒ +... A or P ⇒ +... aQ}
(2) Experimental steps
(1) Construct the FIRSTVT set and LASTVT set of grammar G
Grammar:
B - > J x (J x) * | x (J x) * (expression)
X - > y (C, y) * (item)
Y - > I | n | (b) (factor)
J - > + | - (addition operator)
C - > * | / (multiplication operator)
FIRSTVT set:
FIRSTVT (expression) = {+, -, (,, /, identifier, unsigned integer}
FIRSTVT (item) = {, /, (, identifier, unsigned integer}
FIRSTVT (factor) = {, identifier, unsigned integer}
Frtstvt (addition operator) = {+, -}
Frtstvt (multiplication operator) = {, /}
LASTVT set:
LASTVT (expression) = {+, -,),, /, identifier, unsigned integer}
LASTVT (item) = {, /,), identifier, unsigned integer}
LASTVT (factor) = {), identifier, unsigned integer}
(2) Construct priority relation table
(3) Construction general control program
Algorithm priority analysis algorithm is described as follows:
stack S;
k = 1; // Usage depth of symbol stack S
S[k] = '#'
REPEAT
Read the next input symbol into a;
If S[k]∈ VT then j = k else j = k-1;
While S[j] > a do
Begin
Repeat
Q = S[j];
if S[j-1] VT then j = j-1 else j = j-2
until S[j] < Q;
Reduce S[j+1]... S[k] to some N and output which symbol to reduce;
K = j+1;
S[k] = N;
end of while
if S[j] < a or S[j] = a then
begin k = k+1; S[k] = a end
else error / / call the error diagnosis program
until a = '#'
Explanation of the algorithm: what is stored in a is the terminator in the currently analyzed sentence. Constantly compare the priority of the first terminator s[j] at the top of the stack with that in a. If s[j] priority is lower than or the same as a, the terminator in a is put on the stack; If the priority of s[j] is higher than a, look down in the stack until the terminator with lower priority than s[j] is found. Suppose it is represented by b, and then reduce the string above b in the stack (that is, the leftmost prime phrase) to N (pop up the string above b in the stack, and N into the stack). At this time, the top terminator b of the stack is the new s[j]. Then compare the priorities of the top terminators s[j] and a, and repeat the above steps.
(4) Algorithm flow chart

4, Source program and debugging results
1. Source code:
#include <iostream>
#include<bits/stdc++. h> / / Universal header file
using namespace std;
#define M 9
// Operator precedence relation table
int findP(int a, int b) // a. b ∈ [1,9], starting from 1
{
int table[M][M] = // 1 means priority is higher than, - 1 means priority is lower than, 0 means priority is equal to, and 2 means empty
{
{0,0,-1,-1,-1,-1,-1,1,1},
{0,0,-1,-1,-1,-1,-1,1,1},
{1,1,0,0,-1,-1,-1,1,1},
{1,1,0,0,-1,-1,-1,1,1},
{1,1,1,1,0,2,2,1,1},
{1,1,1,1,2,0,2,1,1},
{-1,-1,-1,-1,-1,-1,-1,0,1},
{1,1,1,1,2,2,0,1,1},
{-1,-1,-1,-1,-1,-1,-1,-1,0}
};
return table[a-1][b-1]; //Array subscripts start at 0
}
// Judge whether c is a terminator. Instead of returning 0, it returns its line number in the priority relationship table (starting from 1)
int Is_Vt(char c)
{
int n;
switch(c)
{
case 'p':
n=1;
break; //plus +
case 'm':
n=2;
break;//minus -
case 't':
n=3;
break;//times *
case 's':
n=4;
Break;//slash /
case 'i':
n=5;
break;//ident
case 'n':
n=6;
break;//number
case 'l':
n=7;
break;//lparen (
case 'r':
n=8;
break;//rparen )
case '#':
n=9;
break;
default:
n=0;
}
return n;
}
void Getinputs(char* inputs)//input
{
int i = 0;
string line;
while(cin >> line)
{
inputs[i++] = line[1];
}
inputs[i] = '#';
}
// Judge the validity of the expression, p points to the head of the analysis stack and k points to the top of the stack; psc points to the current input symbol
int judge(char* p, int k, char* psc)
{
//The current input symbol is an operator, while the top of the stack is #, and there is no operand in front of the operator
if(k == 1 && p[k] == '#' && (*psc == 'p' || *psc == 'm' || *psc == 't' || *psc == 's'))
{
return 0;
}
//The current input symbol is #, the last input symbol is an operator, and there is no operand after the operator
if(*psc == '#' && (*(psc-1) == 'p' || *(psc-1) == 'm' || *(psc-1) == 't' || *(psc-1) == 's'))
{
return 0;
}
//Adjacent operation symbols
if(((*psc == 'p' || *psc == 'm' || *psc == 't' || *psc == 's') && ((*(psc+1) == 'p' || *(psc+1) == 'm' || *(psc+1) == 't' || *(psc+1) == 's'))))
{
return 0;
}
return 1;
}
int main()
{
char s[30] = {'\0'};//Analysis stack s
int k = 1; // k points to the top of the stack
s[k] = '#';
s[k+1] = '\0';
int j; // j terminal pointing to the top of the stack
char q; // q refers to the element pointed to by j, that is, the stack top terminator
// Input processing
char inputs[100] = {'\0'}; // Input string
Getinputs(inputs);
//printf("string is:% s\n", inputs);
char *psc = inputs; // Points to the current input symbol
int flag; // The value obtained by looking up the operator priority relation table (1 / - 1 / 0 / 2) (greater than / less than / equal to / empty)
// Operator priority analysis algorithm general control program
while(1)
{
if(!judge(s, k, psc)) //The expression is illegal and an error is reported directly
{
printf("No,it is wrong.");
exit(1);
}
// Let j point to the top of the stack Terminator
if(Is_Vt(s[k]))
j = k;
else
j = k-1;
// Compare the priority relationship between s[j] and * PSC (current input symbol) to determine whether to move in or protocol
flag = findP(Is_Vt(s[j]), Is_Vt(*psc));
if(flag == 1) // s[j] priority is higher than * psc, and the protocol is implemented
{
//Look down in the top of the stack until you find a terminator with a priority lower than s[j]
do
{
q = s[j];// q save current Terminator
// j go down one (two) step to find the next Terminator
if(Is_Vt(s[j-1]))
j--;
else
j-=2;
}
while(findP(Is_Vt(s[j]), Is_Vt(q)) != -1);
k = j+1;
s[k] = 'N'; // Reduce the strings above Q (excluding q) in the stack to N
s[k+1] = '\0';
continue;
}
else if(flag == -1) // s[j] priority is lower than * psc, move in
{
k++;
s[k] = *psc;
s[k+1] = '\0';
psc++;
continue;
}
else if(flag == 0)
{
if(s[j] == '#')
{
printf("Yes,it is correct.");
break;
}
else // Otherwise move in
{
k++;
s[k] = *psc;
s[k+1] = '\0';
psc++;
continue;
}
}
else // Empty place in priority relation table
{
printf("No,it is wrong.");
exit(1);
}
}
return 0;
}
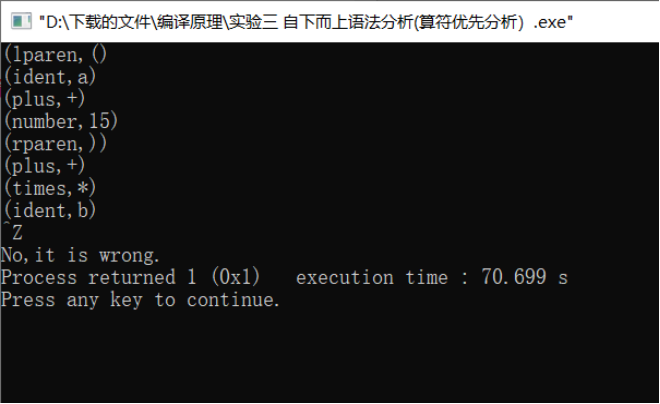
2. Screenshot of program operation results
Test data I:

Test data 2: