More algorithm solutions, please pay attention to the official account, "programmer"

Sorting of single linked list

Problem description

LeetCode 148. Sorting linked list

Given an unordered single linked list with n nodes, it is sorted in ascending order.

Requirements: space complexity O(n), time complexity O(nlogn).

Example:

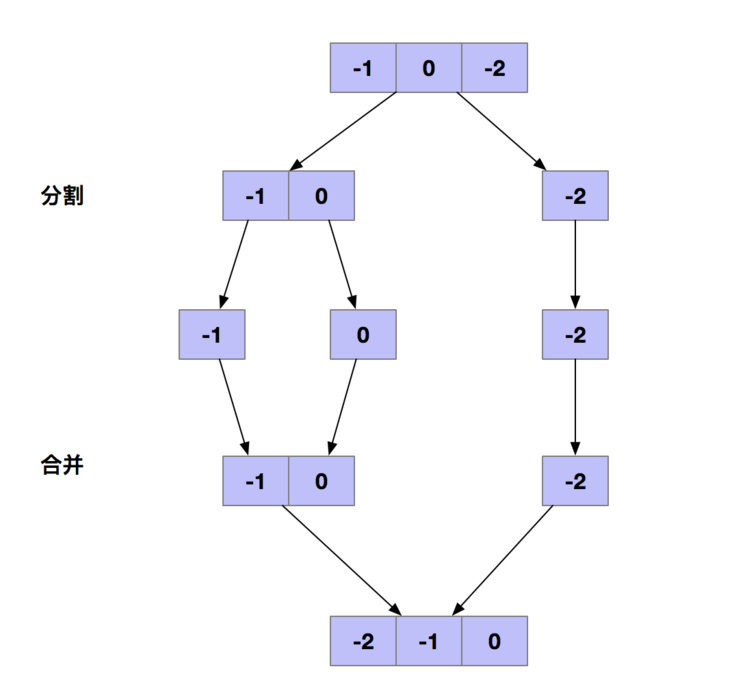
Input: [- 1,0, - 2]

Return value: {- 2, - 1,0}

Analyze problems

Because the topic requires that the time complexity is O(nlogn), the sorting algorithms with time complexity of O(nlogn) include merge sorting, quick sorting and heap sorting, among which the most suitable sorting algorithm for linked list is merge sorting.

Merge sort is based on the idea of divide and conquer. The easiest thing to think of is the top-down recursive implementation. The top-down recursive implementation mainly includes two links.

1. Split link

   • Find the midpoint of the linked list, take the midpoint as the boundary, and split the linked list into two sub linked lists. The fast and slow pointer method can be used to find the midpoint of the linked list. The fast pointer moves 2 steps each time and the slow pointer moves 1 step each time. When the fast pointer reaches the end of the linked list, the slow pointer just points to the midpoint of the linked list.
   • After finding the midpoint, cut the linked list into two sub linked lists at the midpoint.
   • Then recursively split until the split linked list has only one node or is Null. At this time, the split sub linked list is ordered because it contains only one node.

2. Merge link

   • Merge two ordered linked lists into an ordered linked list. We can use the double finger needle method.
   • Execute recursively until the merge is complete.

class Solution:
    def sortList(self, head):
        #If the linked list is empty or contains only one node, recursion terminates
        if not head or not head.next:
            return head
        #Use the fast and slow pointer method to find the midpoint of the linked list
        slow=head
        fast=head.next
        while fast and fast.next:
            fast=fast.next.next
            slow=slow.next
        #slow points to the midpoint of the linked list. The linked list is divided at the midpoint
        head2=slow.next
        slow.next=None
        #Recursive cut split linked list
        left = self.sortList(head)
        right = self.sortList(head2)
        #Merge the linked list and use the double finger needle method
        tmp = res = ListNode(0)
        while left and right:
            if left.val < right.val:
                tmp.next=left
                left=left.next
            else:
                tmp.next=right
                right=right.next
            tmp=tmp.next
        if left:
            tmp.next=left
        else:
            tmp.next=right
        return res.next

The time complexity of the algorithm is O(n). Since top-down is implemented by recursion, if the stack space of recursive call stack is considered, the space complexity of the algorithm is O(logn).

optimization

We can also use the bottom-up method to solve it.

First, we find the length of the linked list. Then split the linked list into sub linked lists for merging.

1. We use sublength to represent the length of the sub linked list to be sorted each time. Initially, sublength=1.
2. Each time, the linked list is divided into several sub linked lists with a length of sublength (the length of the last sub linked list may be less than sublength), and the two sub linked lists are combined as a group. After the combination, several ordered sub linked lists with a length of sublength 2 can be obtained (the length of the last sub linked list may be less than sublength 2).
3. Double the value of sublength, repeat the second step, and then merge the longer ordered sub linked list until the length of the ordered sub linked list is greater than or equal to the length of the linked list, so that the sorting of the whole linked list is completed.

Let's look at the implementation of the code.

class Solution:
    def sortList(self, head):
        #Merge two ordered linked lists
        def merge(head1, head2):
            #Sentinel Nodes 
            dummyHead = ListNode(0)
            temp=dummyHead

            while head1 and head2:
                if head1.val <= head2.val:
                    temp.next = head1
                    head1 = head1.next
                else:
                    temp.next = head2
                    head2 = head2.next
                temp = temp.next
            if head1:
                temp.next = head1
            else:
                temp.next = head2

            return dummyHead.next

        #If the linked list is empty, return directly
        if not head:
            return head
        #Traverse the linked list and find the length of the linked list
        length = 0
        node = head
        while node:
            length += 1
            node = node.next

        #Create a sentinel node that points to the chain header
        dummyHead = ListNode(0)
        dummyHead.next=head

        #Initially, the length of the sub linked list is 1
        subLength = 1

        while subLength < length:

            prev=dummyHead
            cur=dummyHead.next

            while cur:
                #Intercept the sub linked list head1 with the length of subLength
                head1 = cur
                for i in range(1, subLength):
                    if cur.next:
                        cur = cur.next
                    else:
                        break

                head2 = cur.next
                cur.next = None

                #Intercept the sub linked list head2 with the length of subLength
                cur = head2
                for i in range(1, subLength):
                    if cur and cur.next:
                        cur = cur.next
                    else:
                        break

                #The remaining linked list nodes after interception
                surplus_head = None
                if cur:
                    surplus_head = cur.next
                    cur.next = None
                #Merge two ordered linked lists
                merged = merge(head1, head2)
                #Insert the ordered linked list into the newly generated linked list
                prev.next = merged

                #Move the pointer to the end of the linked list
                while prev.next:
                    prev = prev.next

                #Continue merging the remaining nodes
                cur=surplus_head
            subLength = subLength * 2

        return dummyHead.next

The time complexity of the algorithm is O(nlogn) and the space complexity is O(1).