Problem background
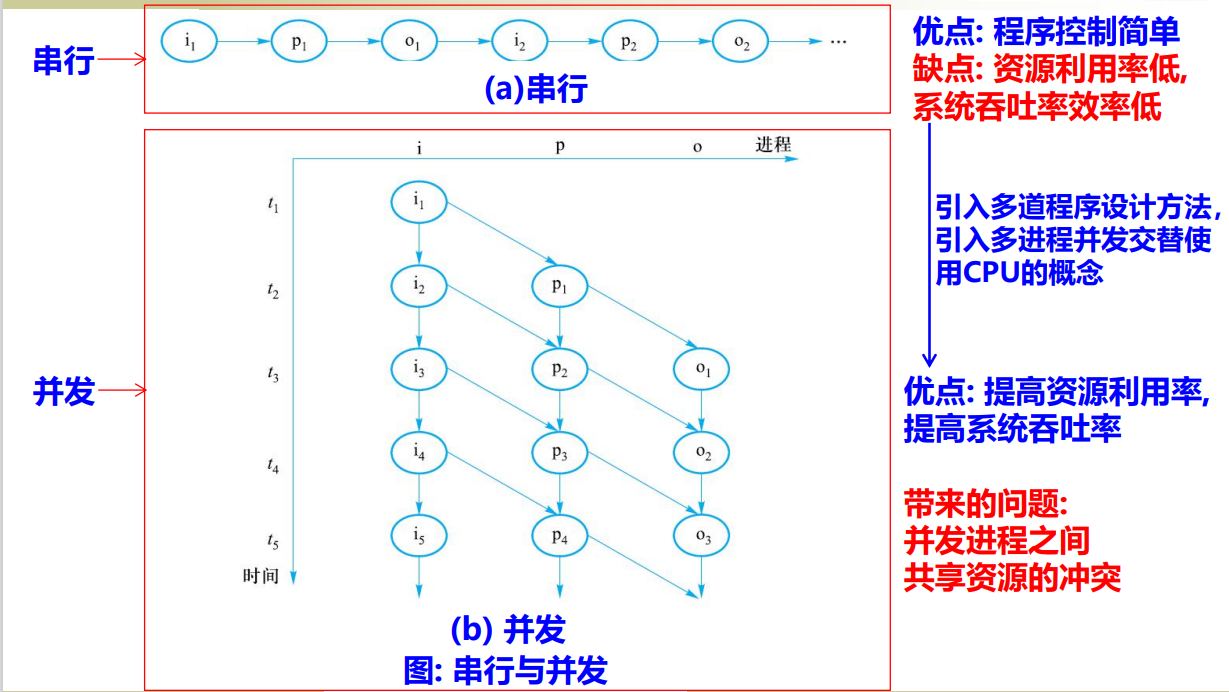
Basic concepts of concurrent programming
Concurrent programming
Critical resources and critical areas, synchronization and mutual exclusion
Critical resources: shared resources that need to be mutually exclusive between concurrent programs
- For example, the toilet on the train
- Use shared variables to represent shared resources
- The program segments related to shared variables in concurrent processes are called critical sections
- Critical area: a program segment that controls the use of shared resources between concurrent processes
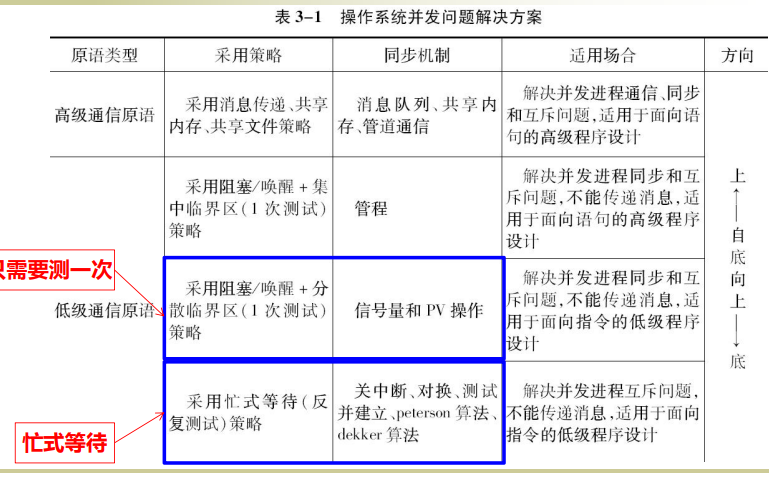
The disadvantage of "busy waiting" in solving the critical area scheduling problem
- Simple method of critical area management (busy waiting / repeated testing)
- Off interrupt
- Test and establish instructions
- Exchange instruction
- Peterson algorithm
- problem
- For the process that cannot enter the critical area, the busy waiting test method is adopted, which wastes CPU time
- The responsibility of whether the test can enter the critical area is handed over to each competitive process, which weakens the reliability of the system and increases the programming burden of users (this reminds me of CPP advanced programming last year. Isn't this the problem of aircraft scheduling? But I didn't know anything about concurrent programming at that time...)
- General solution: semaphore and PV operation
Knowledge framework
Basic principles of PV operation
brief introduction
- Dutch "proberen" and "verhogen"
- Semaphore
Semaphores and PV data structures and primitive operations
Semaphore data structure definition
Let s be a record type data structure, with one component as int value and the other as semaphore queue
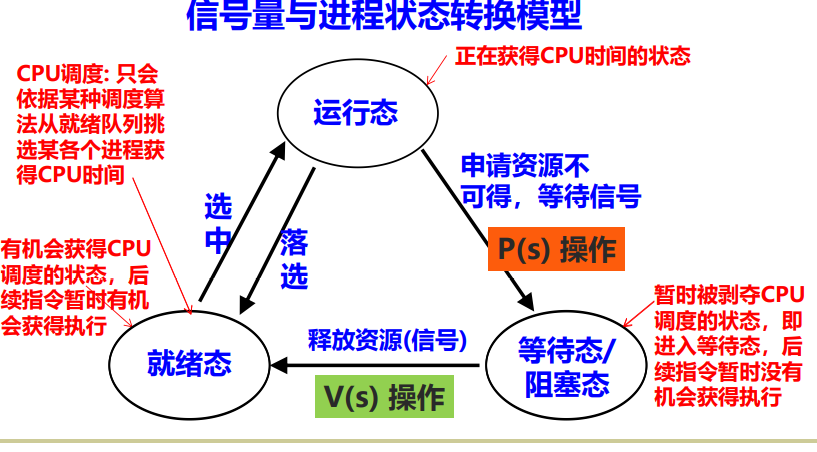
- P(s): semaphore s minus one. If the result is less than zero, it means that the caller cannot get the resource, enters the state of waiting for semaphore s, and moves into the waiting queue of S
- V(s): semaphore s plus one. If the result is not greater than zero, it indicates that there are still processes waiting for resources at this time. Release (wake up) a process from the waiting queue of S and convert it to ready state
- Primitive: a sequence of instructions executed by the CPU in the kernel state in the off interrupt environment Atomicity: a sequence of instructions that can be executed in a safe environment without being interrupted (it seems that I didn't pay attention to turning off the interrupt in Lab4 of OS? I thought too much and looked carefully. The interrupt was already turned off during interrupt processing)

My semaphore and PV code implementation
typedef enum {
RUNNABLE, // Ready. The process at the head of the ready queue is in execution state
TIMED_WAITING,//
WAITING,
BLOCKED
} STATE;
// Array implemented queue
typedef struct s_queue{
PROCESS* procs[NR_TASKS]; // Array of process pointers, NR_TASKS is the number of processes (user processes and system tasks are not strictly distinguished in this experiment)
int begin; // Team leader
int length; // Team tail
} QUEUE;
// Semaphore
typedef struct s_semaphore {
int value; // Value of semaphore
QUEUE queue; //Waiting queue
} SEMAPHORE;
void enqueue(QUEUE *q,PROCESS*proc){
q->procs[(q->begin+q->length++)%NR_TASKS] = proc;
}
PROCESS* dequeue(QUEUE*q){
PROCESS* p;
q->length--;
p = q->procs[q->begin];
q->begin = (q->begin+1)%NR_TASKS;
return p;
}
void P(SEMAPHORE*s){
// If you have enough resources, go straight away
if(--(s->value)>=0){return;}
// The current process is set as blocking, moving out of the ready queue and into the waiting queue of s
p_proc_ready->state=BLOCKED;
dequeue(&readyQueue);
enqueue(&(s->queue),p_proc_ready);
// Immediate scheduling
schedule();
}
void V(SEMAPHORE*s){
if(++(s->value)>0){
// This indicates that no process is waiting for this resource
return;
}
// Wake up blocked processes
PROCESS*p = dequeue(&(s->queue));//Resources available to team leaders
p->state = RUNNABLE;
enqueue(&readyQueue,p);
schedule();
}
Semaphore and process state transition model and its queue model
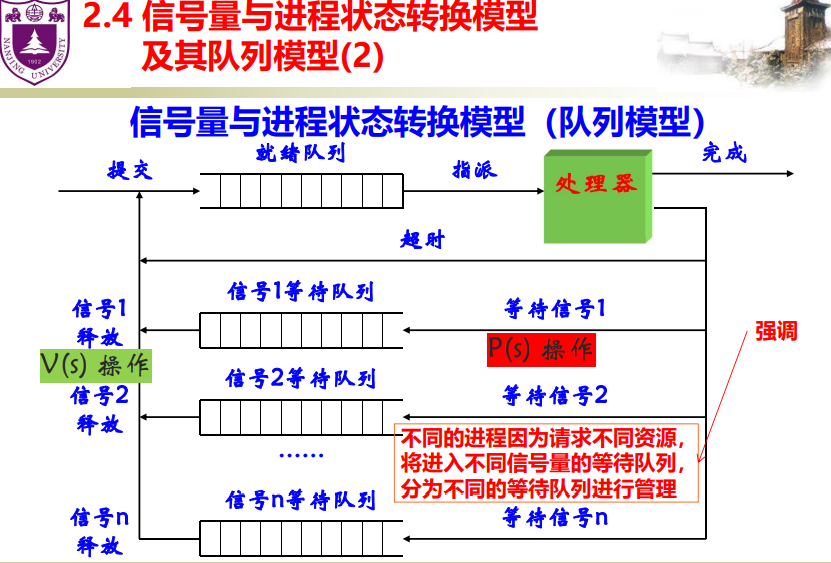
Inference between semaphore and PV operation
- S is a positive number, which is equal to the number of P operations that can be performed by the semaphore s before blocking the process, and also equal to the number of physical resources that can be used in the century represented by S
- s is a negative number, and the absolute value is equal to the number of processes queued in the waiting queue of s
- P stands for requesting a resource and V stands for releasing a resource; Under certain conditions, P represents blocking process operation, and V represents waking up blocked process operation
General structure of semaphore program

PV solving mutual exclusion problem
Dining problem of philosophers
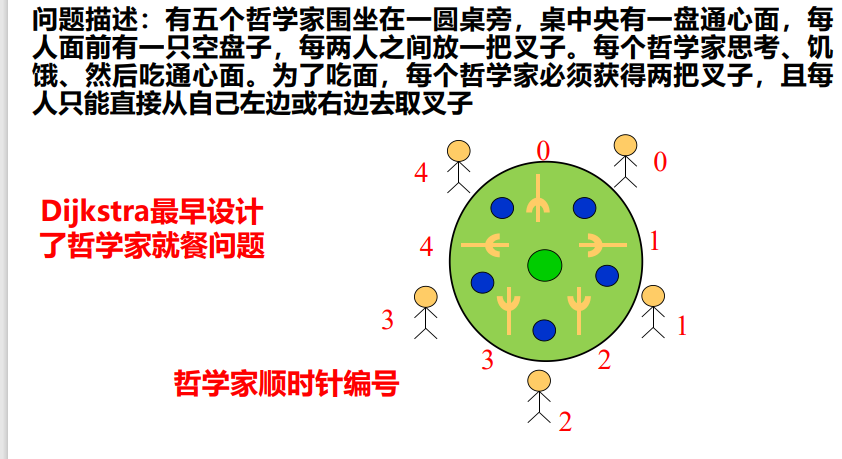
At most four philosophers take forks at the same time
Only one person is allowed to hold the left and right forks at a time
semaphore forks[5];
for(int i=0; i<5; i++)
fork[i]=1;
semaphore mutex = 1; // mutex
process philosopher(int i){ //i=0,1,2,3,4
while(1){
think();
hungry();
P(mutex);
P(fork[i]); // Ask for the fork on the right
P(fork[(i+1)%5]; // Ask for the fork on the left
V(mutex); // Release, because multiple philosophers are allowed to eat at the same time
eat();
V(fork[i]);
V(fork[(i+1)%5];
}
}Even numbered philosophers start from right to left, and odd numbered philosophers start from left to right
semaphore forks[5];
for(int i=0; i<5; i++)
fork[i]=1;
process philosopher(int i){ //i=0,1,2,3,4
while(1){
if(i%2){
// Odd number
P(fork[(i+1)%5]; // Ask for the fork on the left
P(fork[i]); // Ask for the fork on the right
eat();
V(fork[i]);
V(fork[(i+1)%5];
} else {
// even numbers
P(fork[i]); // Ask for the fork on the right
P(fork[(i+1)%5]; // Ask for the fork on the left
eat();
V(fork[i]);
V(fork[(i+1)%5];
}
}
}PV solving synchronization problem
producer consumer problem
No matter what kind of routine is similar, take one, multiple buffer units, multi-level producers and consumers every time you produce several products... For a group of producers and consumers, set an empty semaphore to indicate how many products can be put in the buffer; A full semaphore indicates how many times the product can be fetched from the buffer
It involves the change of counting quantity and needs to be mutually exclusive
Example: multiple producers, multiple consumers and k buffer units. Producers put one product at a time and consumers take one at a time
semaphore empty = k; // Can still put k this product
semaphore full = 0; // The buffer is empty at the beginning
// The buffer can be regarded as a queue, and each unit can be regarded as independent, so there is no need for producers and consumers to be mutually exclusive, but
// If you limit the number of processes that use the buffer at the same time, like the warehouse problem, you have to add a mutex
int head = 0;
int tail = 0;
Product buf[k];
semaphore mutex1 = mutex2 = 1; // Producers and consumers are mutually exclusive
//m producers
process producer(){
while(true){
product = makeProduct();
P(empty); // You can only put it if you have a place
P(mutex1);
head = (head+1)%k;
buf[head] = product;
V(mutex1);
V(full); // Inform consumers that they can take things
}
}
// n consumers
process cosumer(){
while(true){
P(full); // There's something to take
P(mutex2);
product = buf[tail];
tail = (tail+1)%k;
V(empty); // Inform the producer that things can be put
V(mutex2);
}
}
Orange apple problem, farmer Hunter problem, smoker problem
It feels like a variant of the producer consumer problem. The characteristic is that specific consumers consume specific producers, so you only need to set different semaphores for different products
semaphore sp = 1; // Put a fruit on the plate
semaphore s1 = s2 = 0; // There are 0 apples and 0 oranges on the plate
process father(){
P(sp);
// Put oranges
V(s2);
}
process mother(){
P(sp);
// Put apples
V(s1);
}
process daughter(){
P(s2);
// Eat oranges
V(sp);
}
process son(){
P(s1);
// Eat apples
V(sp);
}
semaphore empty = 1; // The cigarette supplier can put it once at first
semaphore s1=s2=s3=0; // Three people can't take it
process producer(){
// There are three kinds of situations: put tobacco matches, match paper, or tobacco paper
int i=RAND()%3;
P(empty);
switch(i){
case 0:
V(s1);
break;
case 1:
V(s2);
break;
case 2:
V(s3);
break;
}
}
// smoker
process consumer(){
// The signals of three smokers are different
P(s_k);
// Take things and assemble cigarettes
V(empty);
}