Above, we used pytorch to build BP neural network. This time, we will build CNN's classic network LeNet or MNIST dataset. The specific data acquisition methods are not introduced in detail in this paper, but only how to build a model and train the dataset. LeNet neural network was proposed by Yan LeCun, one of the three giants of deep learning. He is also the father of convolutional neural networks (CNN). LeNet was first used in handwritten numeral recognition, and the effect is good. It mainly includes the convolution layer, pool layer, full connection layer, etc. the concept is not explained here, but how to build the model. These contents may be introduced later.
1. Network structure
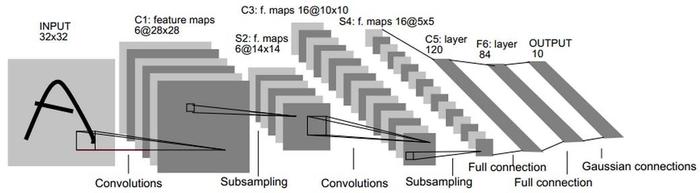
The picture is taken from the paper.
According to the network architecture, the input dimension in the model is 32 * 32 and the output dimension is 1 * 10.
| network layer | input | Convolution kernel | Number of convolution kernels | output |
| Input layer | 32*32*1 | / | / | / |
| C1 layer convolution layer | 32*32*1 | 5*5 | 6 | 28*28*6 |
| S2 layer - pool layer | 28*28*6 | 2*2 | / | 14*14*6 |
| C3 layer convolution layer | 14*14*6 | 5*5 | 16 | 10*10*16 |
| S4 layer - pool layer | 10*10*16 | 2*2 | / | 5*5*16 |
| C5 floor - full connection floor | 5*5*16 | / | / | 1*120 |
| C6 layer - full connection layer | 1*120 | / | / | 1*84 |
| Output layer | 1*84 | / | / | 1*10 |
Build with pytorch according to the above structure:
import torch
from torch import nn
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.c1 = nn.Sequential(
nn.Conv2d(1, 6, (5,5),stride=1,padding=0),
nn.ReLU()
)
self.s2 = nn.MaxPool2d((2,2), padding=0)
self.c3 = nn.Sequential(
nn.Conv2d(6, 16, (5,5),stride=1,padding=0),
nn.ReLU()
)
self.s4 = nn.MaxPool2d((2,2), padding=0)
self.c5 = nn.Sequential(
nn.Linear(5*5*16, 120),
nn.ReLU()
)
self.c6 = nn.Sequential(
nn.Linear(120, 84),
nn.ReLU()
)
self.out = nn.Sequential(
nn.Linear(84, 10),
nn.Sigmoid()
)
def forward(self, x):
x = self.c1(x)
print(x.shape)
x = self.s2(x)
print(x.shape)
x = self.c3(x)
print(x.shape)
x = self.s4(x)
print(x.shape)
x = x.view(-1,5*5*16)
x = self.c5(x)
print(x.shape)
x = self.c6(x)
print(x.shape)
x = self.out(x)
print(x.shape)
return x
inp = torch.randn(1, 1,32,32)
le = LeNet()
out = le(inp)And print the shape of each layer, and the results are as follows:
torch.Size([1, 6, 28, 28]) torch.Size([1, 6, 14, 14]) torch.Size([1, 16, 10, 10]) torch.Size([1, 16, 5, 5]) torch.Size([1, 120]) torch.Size([1, 84]) torch.Size([1, 10])
2. Training model using MNIST dataset
The data set is used to train the model. Other contents are the same as those in the previous section. It is not repeated here, but directly to the code.
import torch
from torchvision import datasets, transforms
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import numpy as np
device = torch.device('cuda:0')
class Config:
batch_size = 128
epoch = 10
alpha = 1e-3
print_per_step = 100 # Control output
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.c1 = nn.Sequential(
nn.Conv2d(1, 6, (5,5),stride=1,padding=0),
nn.ReLU()
)
self.s2 = nn.MaxPool2d((2,2), padding=0)
self.c3 = nn.Sequential(
nn.Conv2d(6, 16, (5,5),stride=1,padding=0),
nn.ReLU()
)
self.s4 = nn.MaxPool2d((2,2), padding=0)
self.c5 = nn.Sequential(
nn.Linear(5*5*16, 120),
nn.ReLU()
)
self.c6 = nn.Sequential(
nn.Linear(120, 84),
nn.ReLU()
)
self.out = nn.Sequential(
nn.Linear(84, 10),
nn.Sigmoid()
)
def forward(self, x):
x = self.c1(x)
x = self.s2(x)
x = self.c3(x)
x = self.s4(x)
x = x.view(-1,5*5*16)
x = self.c5(x)
x = self.c6(x)
x = self.out(x)
return x
class TrainProcess:
def __init__(self):
self.train, self.test = self.load_data()
self.net = LeNet().to(device)
self.criterion = nn.CrossEntropyLoss() # Define loss function
self.optimizer = optim.Adam(self.net.parameters(), lr=Config.alpha)
@staticmethod
def load_data():
train_data = datasets.MNIST(root='./data/',
train=True,
transform=transforms.Compose([
transforms.Resize((32, 32)),transforms.ToTensor()]
),
download=True)
test_data = datasets.MNIST(root='./data/',
train=False,
transform=transforms.Compose([
transforms.Resize((32, 32)), transforms.ToTensor()]
))
# Returns a data iterator
# shuffle: is the order out of order
train_loader = torch.utils.data.DataLoader(dataset=train_data,
batch_size=Config.batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_data,
batch_size=Config.batch_size,
shuffle=False)
return train_loader, test_loader
def train_step(self):
print("Training & Evaluating based on LeNet......")
file = './result/train_mnist.txt'
fp = open(file,'w',encoding='utf-8')
fp.write('epoch\tbatch\tloss\taccuracy\n')
for epoch in range(Config.epoch):
print("Epoch {:3}.".format(epoch + 1))
for batch_idx,(data,label) in enumerate(self.train):
data, label = Variable(data.cuda()), Variable(label.cuda())
self.optimizer.zero_grad()
outputs = self.net(data)
loss =self.criterion(outputs, label)
loss.backward()
self.optimizer.step()
# Print the results every 100 times
if batch_idx % Config.print_per_step == 0:
_, predicted = torch.max(outputs, 1)
correct = 0
for _ in predicted == label:
if _:
correct += 1
accuracy = correct / Config.batch_size
msg = "Batch: {:5}, Loss: {:6.2f}, Accuracy: {:8.2%}."
print(msg.format(batch_idx, loss, accuracy))
fp.write('{}\t{}\t{}\t{}\n'.format(epoch,batch_idx,loss,accuracy))
fp.close()
test_loss = 0.
test_correct = 0
for data, label in self.test:
data, label = Variable(data.cuda()), Variable(label.cuda())
outputs = self.net(data)
loss = self.criterion(outputs, label)
test_loss += loss * Config.batch_size
_, predicted = torch.max(outputs, 1)
correct = 0
for _ in predicted == label:
if _:
correct += 1
test_correct += correct
accuracy = test_correct / len(self.test.dataset)
loss = test_loss / len(self.test.dataset)
print("Test Loss: {:5.2f}, Accuracy: {:6.2%}".format(loss, accuracy))
torch.save(self.net.state_dict(), './result/raw_train_mnist_model.pth')
if __name__ == "__main__":
p = TrainProcess()
p.train_step()It should be emphasized that since the size of MNIST data set is 28 * 28, size conversion is required when reading data.
transforms.Compose([
transforms.Resize((32, 32)), transforms.ToTensor()]
)
Here, we mainly modify the size of the data set and convert the data type to Tensor. The training part can be regarded as a fixed set of templates or processes, which can be used to solve some conventional problems. The training results are as follows:
Training & Evaluating based on LeNet...... Epoch 1. Batch: 0, Loss: 2.30, Accuracy: 8.59%. Batch: 100, Loss: 1.62, Accuracy: 80.47%. Batch: 200, Loss: 1.57, Accuracy: 89.06%. Batch: 300, Loss: 1.56, Accuracy: 90.62%. Batch: 400, Loss: 1.54, Accuracy: 92.97%. Epoch 2. Batch: 0, Loss: 1.52, Accuracy: 92.97%. Batch: 100, Loss: 1.50, Accuracy: 96.88%. Batch: 200, Loss: 1.52, Accuracy: 89.06%. Batch: 300, Loss: 1.50, Accuracy: 92.97%. Batch: 400, Loss: 1.49, Accuracy: 95.31%. Epoch 3. Batch: 0, Loss: 1.50, Accuracy: 94.53%. Batch: 100, Loss: 1.50, Accuracy: 97.66%. Batch: 200, Loss: 1.48, Accuracy: 96.88%. Batch: 300, Loss: 1.50, Accuracy: 95.31%. Batch: 400, Loss: 1.48, Accuracy: 97.66%. Epoch 4. Batch: 0, Loss: 1.47, Accuracy: 96.88%. Batch: 100, Loss: 1.48, Accuracy: 96.88%. Batch: 200, Loss: 1.49, Accuracy: 97.66%. Batch: 300, Loss: 1.48, Accuracy: 98.44%. Batch: 400, Loss: 1.47, Accuracy: 96.88%. Epoch 5. Batch: 0, Loss: 1.47, Accuracy: 100.00%. Batch: 100, Loss: 1.49, Accuracy: 96.88%. Batch: 200, Loss: 1.48, Accuracy: 97.66%. Batch: 300, Loss: 1.48, Accuracy: 96.88%. Batch: 400, Loss: 1.48, Accuracy: 96.88%. Epoch 6. Batch: 0, Loss: 1.47, Accuracy: 98.44%. Batch: 100, Loss: 1.47, Accuracy: 98.44%. Batch: 200, Loss: 1.47, Accuracy: 99.22%. Batch: 300, Loss: 1.47, Accuracy: 99.22%. Batch: 400, Loss: 1.49, Accuracy: 98.44%. Epoch 7. Batch: 0, Loss: 1.48, Accuracy: 97.66%. Batch: 100, Loss: 1.49, Accuracy: 97.66%. Batch: 200, Loss: 1.47, Accuracy: 99.22%. Batch: 300, Loss: 1.48, Accuracy: 98.44%. Batch: 400, Loss: 1.48, Accuracy: 97.66%. Epoch 8. Batch: 0, Loss: 1.48, Accuracy: 98.44%. Batch: 100, Loss: 1.48, Accuracy: 98.44%. Batch: 200, Loss: 1.47, Accuracy: 100.00%. Batch: 300, Loss: 1.48, Accuracy: 98.44%. Batch: 400, Loss: 1.47, Accuracy: 99.22%. Epoch 9. Batch: 0, Loss: 1.46, Accuracy: 99.22%. Batch: 100, Loss: 1.46, Accuracy: 100.00%. Batch: 200, Loss: 1.49, Accuracy: 96.09%. Batch: 300, Loss: 1.47, Accuracy: 97.66%. Batch: 400, Loss: 1.46, Accuracy: 100.00%. Epoch 10. Batch: 0, Loss: 1.47, Accuracy: 98.44%. Batch: 100, Loss: 1.47, Accuracy: 99.22%. Batch: 200, Loss: 1.47, Accuracy: 98.44%. Batch: 300, Loss: 1.47, Accuracy: 99.22%. Batch: 400, Loss: 1.47, Accuracy: 100.00%. Test Loss: 1.49, Accuracy: 98.39%
Compared with the previous BP network.