1 stack

1.1 stack introduction

1. stack is a container adapter, which is specially used in the context of last in first out operation. Its deletion can only insert and extract elements from one end of the container.
2. Stack is implemented as a container adapter. A container adapter encapsulates a specific class as its underlying container, and provides a set of specific member functions to access its elements. With a specific class as its underlying element, the tail of a specific container (i.e. the top of the stack) is pushed in and popped out.
3. The underlying container of stack can be any standard container class template or some other specific container classes. These container classes should support the following operations: Empty: empty operation, back: get tail element operation, push_back: tail insert element operation, pop_back: delete element at the end
4. The standard containers vector, deque and list meet these requirements. By default, if no specific underlying container is specified for stack, deque is used by default.

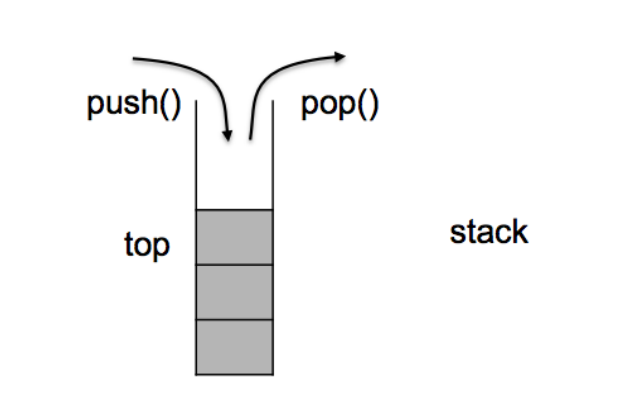
1.2 stack usage

Interface description

1.3 stack simulation implementation

namespace czh
{
	template<class T, class Container = deque<T>>
	// template<class T, class Container = list<T>>
	// template<class T, class Container = vector<T>>
	class stack
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_back();
		}
        T& top()
		{
			return _con.back();
		}
		const T& top() const
		{
			return _con.back();
		}

		size_t size() const
		{
			return _con.size();
		}

		bool empty() const
		{
			return _con.empty();
		}

	private:
		Container _con;
	};
}

1.4 brief introduction of deque

principle

1. Deque (double ended queue): it is a data structure of "continuous" space with double openings. Note that it has nothing to do with queue. The meaning of double openings is that insertion and deletion can be carried out at both ends of the head and tail, and the time complexity is O(1). Compared with vector, the head insertion efficiency is high, and there is no need to move elements; Compared with list, the space utilization rate is relatively high.
2. Deque is not really a continuous space, but is composed of continuous small spaces. The actual deque is similar to a dynamic two-dimensional array

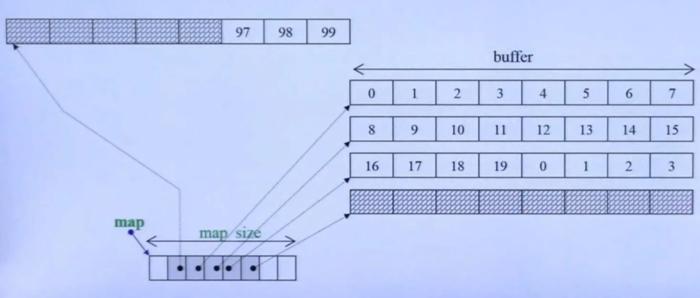
3. The bottom layer of the double ended queue is an imaginary continuous space, which is actually piecewise continuous. In order to maintain its "overall continuity" and the illusion of random access, it falls on the iterator of deque. Therefore, the iterator design of deque is more complex, as shown in the following figure:

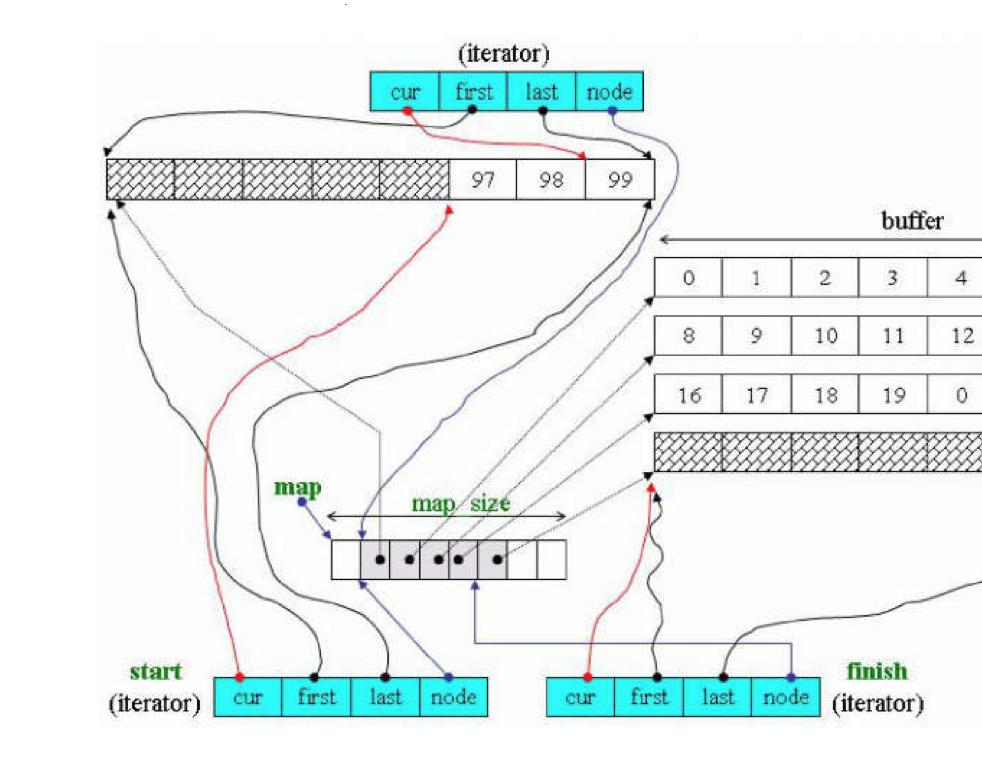
defect

• Compared with vector, deque has the following advantages: it does not need to move elements during header insertion and deletion, which is particularly efficient. Moreover, it does not need to move a large number of elements during capacity expansion, so its efficiency is higher than vector.
• Compared with list, its bottom layer is continuous space, which has high space utilization and does not need to store additional fields.
• However, deque has a fatal defect: it is not suitable for traversal, because during traversal, the iterator of deque needs to frequently detect whether it moves to the boundary of a small space, resulting in low efficiency. In sequential scenes, it may need to be traversed frequently. Therefore, in practice, when linear structure is required, vector and list are given priority in most cases, and deque is not widely used, One application that can be seen at present is that STL uses it as the underlying data structure of stack and queue.

Why is it the default implementation of stack and queue

• Stack is a special linear data structure of last in first out, so as long as it has push_back() and pop_ The linear structure of back () operation can be used as the underlying container of stack, such as vector and list; Queue is a special linear data structure of first in first out, as long as it has push_back and pop_ The linear structure of front operation can be used as the underlying container of queue, such as list.

However, in STL, deque is selected as its underlying container by default for stack and queue, mainly because:

1. Stack and queue do not need to be traversed (so stack and queue have no iterators). They only need to operate in a fixed section or at both ends.
2. When the elements in stack grow, deque is more efficient than vector (there is no need to move a large amount of data during capacity expansion); When the elements in the queue grow, deque is not only efficient, but also has high memory utilization.

Therefore, combining the advantages of deque, perfect delivery avoids its defects

2 queue

2.1 queue introduction

1. A queue is a container adapter designed to operate in a FIFO context (first in first out), where elements are inserted from one end of the container and extracted from the other end.
2. Queue is implemented as a container adapter, which encapsulates a specific container class as its underlying container class, and queue provides a set of specific member functions to access its elements. Elements enter the queue from the end of the queue and exit the queue from the head of the queue.
3. The underlying container can be one of the standard container class templates or other specially designed container classes. The underlying container should at least support the following operations: Empty: check whether the queue is empty, size: return the number of valid elements in the queue, front: return the reference of the queue head element, back: return the reference of the queue tail element, push_back: enter the queue and pop at the end of the queue_ Front: exit the queue at the head of the queue
4. The standard container classes deque and list meet these requirements. By default, if no container class is specified for queue instantiation, the standard container deque is used.

2.2 queue usage

Interface introduction

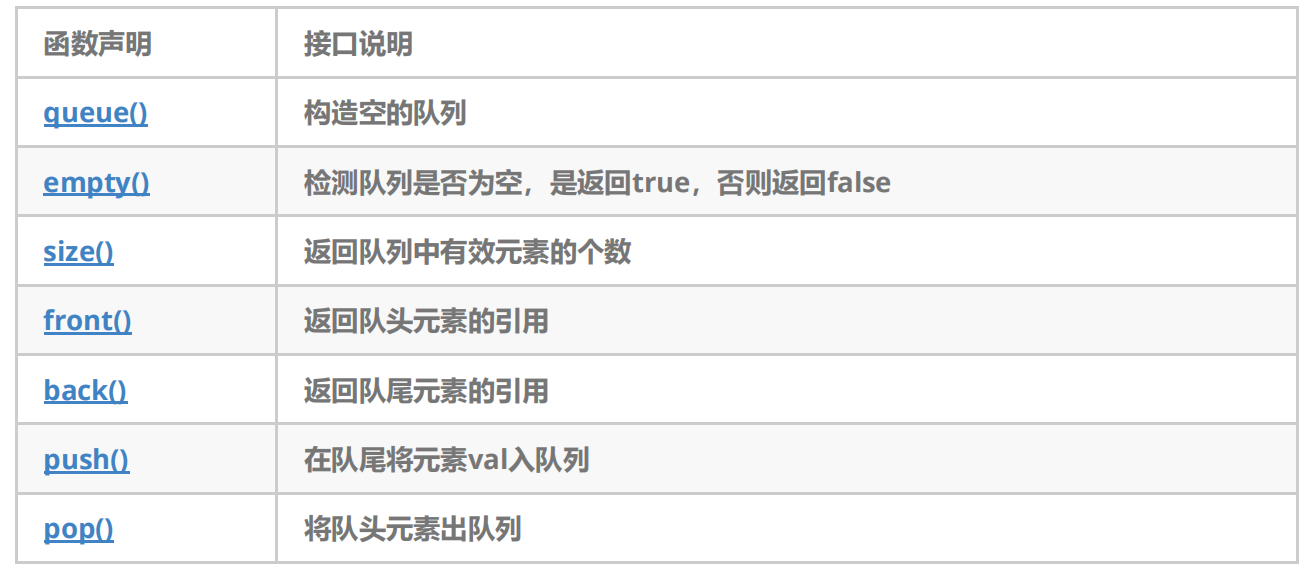
2.3 queue simulation implementation

Because there are header deletion and tail insertion in the interface of queue, it is too inefficient to use vector to encapsulate, so you can simulate the implementation of queue with the help of list and deque

namespace czh
{
	// Design mode -- adapter mode (adapter)
	template<class T, class Container = deque<T>>
	class queue
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_front();
		}
        T& front()
		{
			return _con.front();
		}
		const T& front() const
		{
			return _con.front();
		}
		T& back()
		{
			return _con.back();
		}
		const T& back() const
		{
			return _con.back();
		}

		size_t size() const
		{
			return _con.size();
		}

		bool empty() const
		{
			return _con.empty();
		}

	private:
		Container _con;
	};
}

3 priority_queue

3.1 priority_queue introduction

1. Priority queue is a kind of container adapter. According to the strict weak sorting standard, its first element is always the largest one among the elements it contains.
2. The internal implementation is actually a heap, in which elements can be inserted at any time, and only the largest heap element (the element at the top of the priority queue) can be retrieved.
3. The underlying container can be any standard container class template or other specially designed container classes. The container should be accessible through a random access iterator and support the following operations: empty(): check whether the container is empty, size(): return the number of valid elements in the container, front(): return the reference of the first element in the container and push_back(): insert elements and pop at the end of the container_ Back(): delete the element at the end of the container
4. The standard container classes vector and deque meet these requirements. By default, if there is no specific priority_ If the queue class instantiates the specified container class, vector is used.
5. Random access iterators need to be supported in order to always maintain the heap structure internally. The container adapter automatically calls the algorithm function when needed_ heap,push_heap and pop_heap to do this automatically.

3.2 priority_queue usage

By default, the priority queue uses vector as its underlying data storage container, and heap algorithm is used on the vector to form the heap structure of the elements in the vector, so priority_queue is the heap, so priority can be considered for all locations that need to use the heap_ queue. Note: default priority_queue is a lot. The heap can be changed to a small function.

#include <iostream>
#include <vector>
#include <queue>
#Include < functional > / / header file of greater algorithm
void TestPriorityQueue()
{
 // By default, a lot is created, and its bottom layer is compared according to the less than sign
 vector<int> v{3,2,7,6,0,4,1,9,8,5};
 priority_queue<int> q1;
 for (auto& e : v)
 q1.push(e);
 cout << q1.top() << endl;
 // If you want to create a small heap, change the third template parameter to greater comparison mode
 priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end());
 cout << q2.top() << endl; 
 
 }

3.3 introduction of imitative function

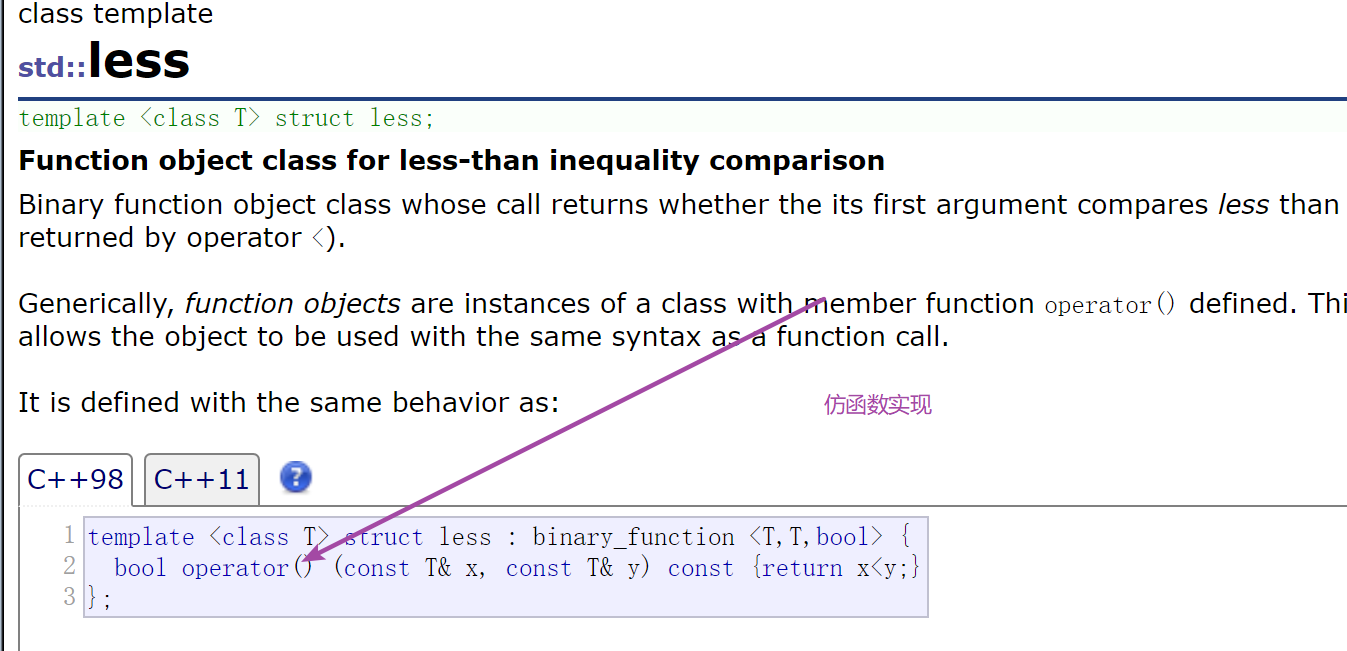
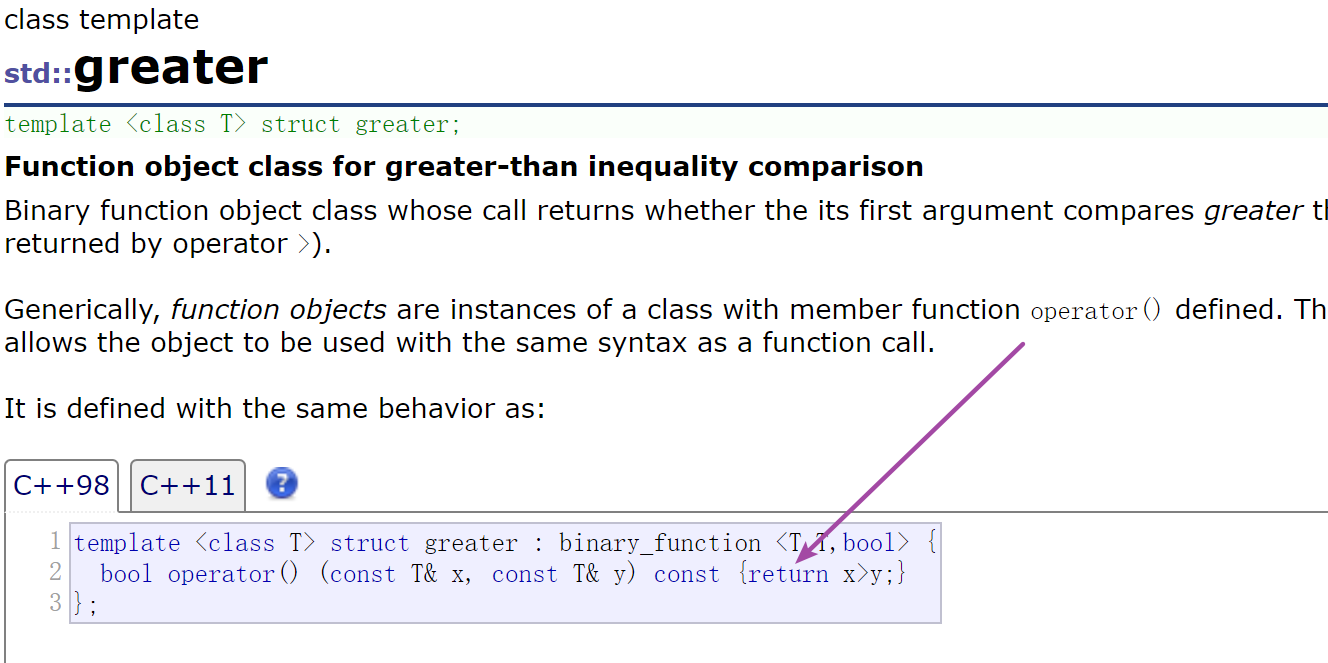
The imitation function is exactly a class. This class overloads operator(). The object of this class calls operator(), which can be used like a function. The use in the priority queue can control whether there is a large pile or a small pile in the created priority queue, so that it can control hot water or cold water like the switch of the water tap. The implementation of two imitation functions in STL library is as follows:

Priority queue in STL

An example is given to illustrate the application of imitation function

For example, if we want to buy a mobile phone and search for a mobile phone on jd.com, we can sort it according to the price, sales volume and other labels. Then we can use the imitation function to simply implement it and write a commodity class to represent the mobile phone. We use the sorting algorithm sort to sort it, but we can't overload the > < operator inside the class, because we don't know how to sort and according to what standard, In order to better explain the problem, the disk code.

#include <iostream>
#include "priority_queue.h"
#include <algorithm>
#include <vector>

using namespace std;

//Application of imitative function
struct Phone{
	int saleNum;
	int price;
	//.....
};
struct LessPhonePrice{
	bool operator()(const Phone& p1, const Phone& p2)
	{
		return p1.price < p2.price;
	}
};
struct LessPhoneSaleNum{
	bool operator()(const Phone& p1, const Phone& p2)
	{
		return p1.saleNum < p2.saleNum;
	}
};
void TestSort()
{
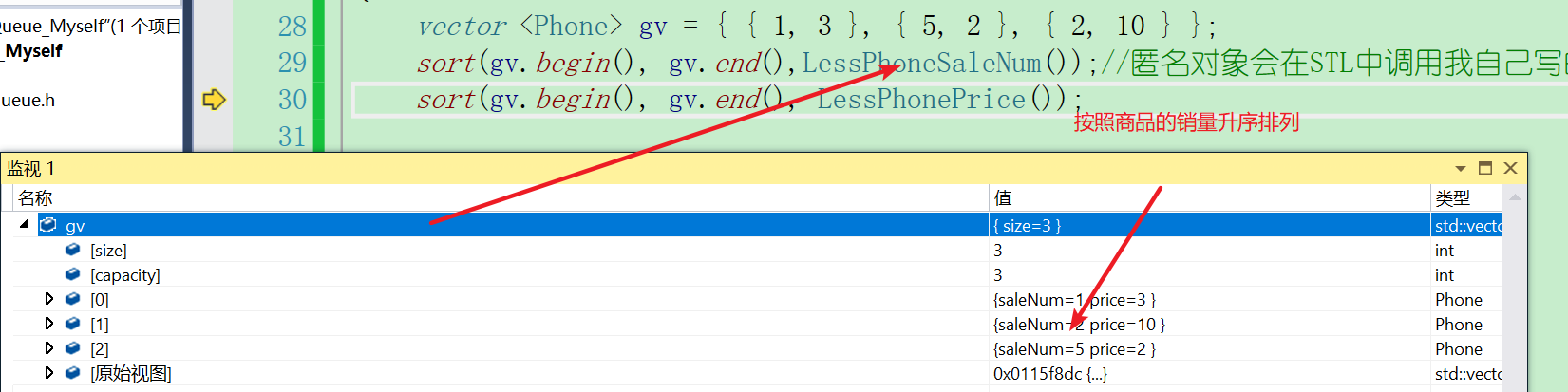
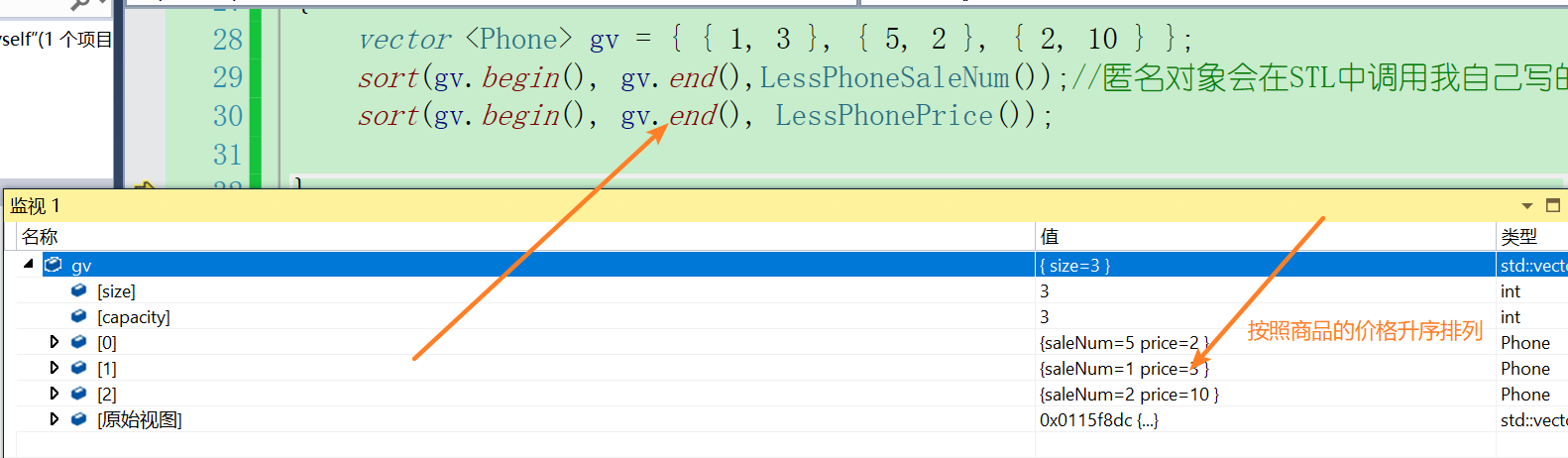
	vector <Phone> gv = { { 1, 3 }, { 5, 2 }, { 2, 10 } };
	sort(gv.begin(), gv.end(),LessPhoneSaleNum());//Anonymous objects will call my own comparison method in STL.
	sort(gv.begin(), gv.end(), LessPhonePrice());

}
int main()
{
	TestSort();
	return 0;
}

3.4 priority_queue simulation implementation

Because the underlying structure of priority queue is heap, it is OK to properly encapsulate the vector. If you don't know the knowledge of heap, please refer to another article of mine https://blog.csdn.net/CZHLNN/article/details/112481962

#pragma once

//functor 
template<class T>
class Less{
public:
	bool operator()(const T& t1, const T& t2) const
	{
		return t1 < t2;
	}
};

template<class T>
class Greater{
public:
	bool operator()(const T& t1, const T& t2) const
	{
		return t1 > t2;
	}
};
namespace czh{

	template<class T, class Container = vector<T>, class Compare = Greater<T>>
	class priority_queue {

	public:
		priority_queue() = default;
		/*priority_queue()
		{}*/

		template<class InputIterator>
		priority_queue(InputIterator first, InputIterator last)
			:_con(first, last)
		{
			//Using the downward adjustment algorithm, build the heap from bottom to top
			/*for (int i = (_con.size() - 2) / 2; i >= 0; i--)
			{
			AdjustDown(i);
			}*/
			Use the up adjustment algorithm to adjust from top to bottom
			for (size_t i = 1; i < _con.size(); i++)
			{
				AdjustUp(i);
			}
		}
		void push(const T& data)
		{
			_con.push_back(data);
			// Upward adjustment
			AdjustUp(_con.size() - 1);
		}
		void pop()
		{
			if (empty()) return;

			swap(_con.front(),_con.back());
			_con.pop_back();
			AdjustDown(0);
		}
		size_t size() const
		{
			return _con.size();
		}
		const T& top() const
		{ 
			return _con.front();
		}
		bool empty() const
		{
			return _con.empty();
		}
	private:
		//Upward adjustment algorithm
		void AdjustUp(int child)
		{
			Compare com;
			int parent = (child - 1) >> 1;
			while (child > 0)
			{
				/*if (_con[child] > _con[parent])*/
				if (com(_con[child], _con[parent]))
				{
					swap(_con[child], _con[parent]);
					child = parent;
					parent = (child - 1) >> 1;
				}
				else
				{
					break;
				}
			}
		}
		void AdjustDown(int parent)
		{
			Compare com;
			size_t child = 2 * parent + 1;
			while (child < _con.size())
			{
				/*if (child + 1 < _con.size() && _con[child + 1] < _con[child])*/
				if (child + 1 < _con.size() && com(_con[child + 1], _con[child]))
				{
					child++;
				}
				/*if (_con[child] > _con[parent])*/
				if (com(_con[child], _con[parent]))
				{
					swap(_con[child], _con[parent]);
					parent = child;
					child = 2 * parent + 1;
				}
				else
				{
					break;
				}
			}
		}
		//Downward adjustment algorithm
		Container _con;
	};
}

4 container adapter mode

The design pattern that the majority of users want to know and use is another kind of interface design pattern that the majority of users want to convert into a set of code.
The three data structures described above are container adapter s.