Links: https://ac.nowcoder.com/acm/contest/180/B
Source: Niuke.com

Fireworks
Time limit: C/C++ 1 second, 2 seconds for other languages
Space limit: C/C++ 262144K, other languages 524288K
Special Judge, 64bit IO Format: %lld
Title Description
Little a has nn fireworks, each representing a different color. For the ii fireworks, it has p_ip
i
​
Probability of igniting. Now Small a wants to light them. He wants to know the expected number of colors and the probability of exactly producing kk colors.

Enter a description:
The first row contains two integers n, K n, K
Number of NNs in the next line, number ii p_ip
i
​
Indicates the probability that the ii firework will be ignited
Output description:
The output has two lines
The first line represents the expected number of different colors
The second line represents the probability of producing exactly kk colors
Split with line breaks

Example 1
input
copy
3 2
0.5 0.25 0.75
output
copy
1.5000
0.4062
Explain
The second question explains as an example:
(1, 2) :0.5 * 0.25 * (1 - 0.75) = 0.03125(1,2):0.5∗0.25∗(1−0.75)=0.03125
(1, 3): 0.5 * (1 - 0.25) * 0.75 = 0.28125(1,3):0.5∗(1−0.25)∗0.75=0.28125
(2, 3) :(1 - 0.5) * 0.25 * 0.75 = 0.09375(2,3):(1−0.5)∗0.25∗0.75=0.09375
Add up to 0.406250.40625
Remarks:
For 30%30% of the data: nleqslant 6, kleqslant n n_6,k_n
For 100% 100% of the data: n \leqslant 10^5, k \leqslant 2 * 10^2n_10
5
,k⩽2∗10
2

Keep 4 decimal places for output, if your answer error and std do not exceed 10^{-4}10
−4
Is Right

Topic:

Ideas:

Because each firework contributes 1 to the number of colors,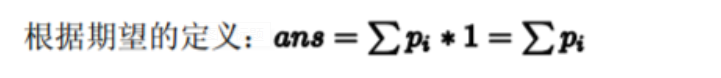

The second output is done with probability dp.

Defines the DP state dp[i][j] to the first firework is the probability that J fireworks have been set.

For each firework there are only two states, lit and not lit, so

The current dp[i][j] = dp[i-1][j-1]a[i]+ dp[i-1][j](1.0000-a[i]), that is, when I-1 fireworks only light J-1 fireworks, I use the probability of a[i] to light the current ith firework, that is, when I-1 fireworks light J fireworks,

Another is that when the ith firework is lit, J fireworks are lit. Current fireworks are not lit, that is, when the ith firework is lit, J fireworks are lit, which together is dp[i][j]

See code for details:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll powmod(ll a,ll b,ll MOD){ll ans=1;while(b){if(b%2)ans=ans*a%MOD;a=a*a%MOD;b/=2;}return ans;}
inline void getInt(int* p);
const int maxn=100010;
const int inf=0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
double a[maxn];
double dp[maxn][202];
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    gbtb;
    cin>>n;
    cin>>k;
    repd(i,1,n)
    {
        cin>>a[i];
    }
    repd(i,1,n)
    {
        repd(j,1,i)
        {
            dp[i][j]+=dp[i-1][j-1]*a[i];
            dp[i][j]+=dp[i-1][j]*(1.0000-a[i]);
        }
    }
    cout<<fixed<<setprecison()
    
    
    
    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}