Title Description:
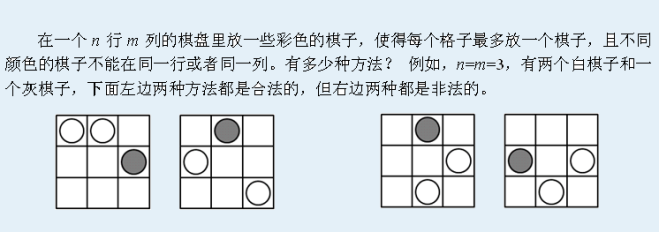
Input format
Enter two integers n, m, c for the first action, i.e. the number of rows, columns and the number of colors of the chess pieces.
The second line contains c positive integers, the number of pieces per color.
The total number of chess pieces of all colors is guaranteed to be no more than nanometer.
N, M<=30 C<=10 The total number of chess pieces is greater than 250
Output format
The output is only one line, that is, the remainder of the total number of solutions divided by 1,000,000,009.
Example
sample input
4 2 2 3 1
sample output
8
Data Scope and Tips
30% n,m<=10
solution:
20%: Search, enumerate all states.
It's said to be the highest search score, but the blogger only got 10 points in the exam, and it's not TLE.
Here's the explanation.
Considering dp, Let f[i][j][k] denote the number of schemes for the first k colors to occupy J column of any I row, and g[i][j][k] denote the number of schemes for all the K colors to occupy J column of any I row.
So first we can get $g [i] [j] [k] = C {i * j} ^ {num [k] - sum {p = 1} ^ {i} sum {q = 1} ^ {j} g [p] [q] [k] * C {i} ^ {P {C {j} {Q q$
In fact, it is to subtract the number of illegitimate (in fact, there are no occupied rows or columns) from the number of legitimate ones.
Next we get the equation of f:
$f[i][j][k] = \sum _ {p = 0} ^ {i - 1} \sum _ {q = 0} ^ {j - 1} f[p][q][k - 1] * g[i - p][j - q][k] * C_{n - p} ^ {i - p} * C_{m - q} ^ {j - q}$
P, q, k-1 is the last state of the enumeration, $C_{n-p}^{i-p}$denotes the selection of I-P players in N-P rows, $C_{m-q}^{i-q}$is the same.
Finally, $ans= sum {i = 1} ^ {m} sum {j = 1} ^ {n} f [i] [j] [c]$, and the problem was solved perfectly.
Place the code:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define mod 1000000009 5 #define ll long long 6 #define MAXNM 905 7 using namespace std; 8 int n,m,c,num[12]; 9 ll C[MAXNM][MAXNM],g[35][35][12],f[35][35][15],ans=0; 10 int main(){ 11 scanf("%d%d%d",&n,&m,&c); 12 for(int i=0;i<=n*m;i++){ 13 C[i][0]=1; 14 for(int j=1;j<=i;j++) 15 C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; 16 } 17 f[0][0][0]=1; 18 for(int k=1;k<=c;k++) 19 scanf("%d",&num[k]); 20 for(int k=1;k<=c;k++){ 21 for(int i=1;i<=n;i++) 22 for(int j=1;j<=m;j++){ 23 if(i*j<num[k]) continue; 24 g[i][j][k]=C[i*j][num[k]]; 25 for(int p=1;p<=i;p++) 26 for(int q=1;q<=j;q++){ 27 if(p<i||q<j) 28 g[i][j][k]=(g[i][j][k]-g[p][q][k]*C[i][p]%mod*C[j][q]%mod)%mod; 29 //cout<<g[i][j]<<endl; 30 } 31 } 32 } 33 for(int k=1;k<=c;k++){ 34 for(int i=1;i<=n;i++) 35 for(int j=1;j<=m;j++) 36 for(int p=0;p<i;p++) 37 for(int q=0;q<j;q++){ 38 int l=i-p,r=j-q; 39 if(l*r<num[k]) continue; 40 f[i][j][k]=(f[i][j][k]+f[p][q][k-1]*g[l][r][k]%mod*C[n-p][l]%mod*C[m-q][r]%mod)%mod; 41 //cout<<f[i][j][k]<<endl; 42 } 43 } 44 for(int i=1;i<=n;i++) 45 for(int j=1;j<=m;j++) 46 ans=(ans+f[i][j][c])%mod; 47 printf("%lld\n",ans); 48 return 0; 49 }
We find that g contributes only to the current chess piece, so the third dimension can be eliminated and g and f are processed at each input.
#include<iostream>
#include<cstdio>
#include<cstring>
#define mod 1000000009
#define ll long long
#define MAXNM 905
using namespace std;
int n,m,c,num[12];
ll C[MAXNM][MAXNM],g[35][35],f[35][35][15],ans=0;
int main(){
scanf("%d%d%d",&n,&m,&c);
for(int i=0;i<=n*m;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
f[0][0][0]=1;
for(int k=1;k<=c;k++){
scanf("%d",&num[k]);
memset(g,0,sizeof(g));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(i*j<num[k]) continue;
g[i][j]=C[i*j][num[k]];
for(int p=1;p<=i;p++)
for(int q=1;q<=j;q++){
if(p<i||q<j)
g[i][j]=(g[i][j]-g[p][q]*C[i][p]%mod*C[j][q]%mod)%mod;
//cout<<g[i][j]<<endl;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int p=0;p<i;p++)
for(int q=0;q<j;q++){
int l=i-p,r=j-q;
if(l*r<num[k]) continue;
f[i][j][k]=(f[i][j][k]+f[p][q][k-1]*g[l][r]%mod*C[n-p][l]%mod*C[m-q][r]%mod)%mod;
//cout<<f[i][j][k]<<endl;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ans=(ans+f[i][j][c])%mod;
printf("%lld\n",ans);
return 0;
}