Relevant code address: https://gitee.com/gudongkun/datestruct
1, What is AOE
AOE(Activity on edge network): in a weighted directed graph representing the project, the vertex represents the event, the directed edge represents the activity, and the weight on the edge represents the duration of the activity. Such a directed graph is called the edge represents the activity network, or AOE network for short
The vertices in the AOE network without edges are called starting points (or source points); Points without edges are called endpoints (or sinks)
2, Properties of AOE networks
- Only after the event represented by a vertex occurs, the activity starting from the vertex can start;
- The event represented by a vertex can occur only when all activities entering a vertex are completed.
3, AOE network can solve the following problems
- At least how long will it take to complete the whole project
- What activities should be accelerated to shorten the time required to complete the project
4, Key activities
Critical path: there may be more than one activity that takes the longest time, so the most important thing is to find the activity that cannot be delayed is called critical activity
If the time of an activity is shortened and the overall end time cannot be changed, the activity is not a key activity; If you shorten the time of an activity, the activity is the key activity.
5, Algorithm description of key activities
1. 4 precursors of key activities
(1) Earliest occurrence time of event A event_early[B] : event_early[B] = max{event_early[BeforeB]+len<BeforeB,B>}
(2) Latest occurrence time of event A event_latest[B]: event_latest[B] = min{event_latest[AfterB]-len<B,AfterB>}
(3) Earliest occurrence time of activity AB activity_early : activity_early[BC] = event_early[B]
(4) Latest occurrence time of activity AB activity_latest : activity_latest[CD] = event_latest[D] - len[CD]
Note: len < A, b > indicates the length of arc AB
[external chain picture transfer failed, and the source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-0eevwxce-1642157321022) (data: image / GIF; Base64, r0lgodlhaqabapabap / / / waaach5baekaaaaaaaaaaabaaaeaaaicraeaow = =)]
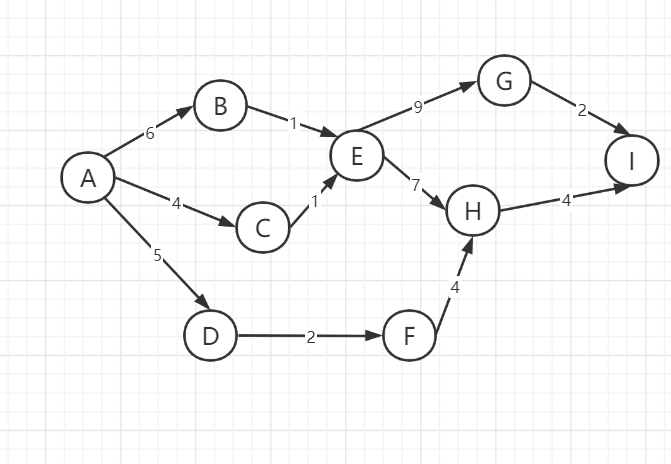
(1) event_early analysis
event : A B C D E F G H I
event_early : 0 6 4 5 7 7 16 14 18
- Starting from the starting point, the starting point time must be 0
- The subsequent events are calculated by the time of the previous event, such as:
- event_early[B] = max{event_early[A]+len<A,B>}
- event_early[E] = max{event_early[B]+len<B,E> ，event_early[C]+len<C,E>}
(2)event_latest analysis, dependent event_early
event : A B C D E F G H I
event_early : 0 6 4 5 7 7 16 14 18
event_latest: 0 6 6 8 7 10 16 14 18
- Calculate from the back to the front, and the end event directly takes event_early
- Use the time of the previous event to calculate, such as event_ latest[B] = min{event_latest[C]-len<A,B>}
- The start time must be 0
(3)activity_early analysis
The earliest start time of activity BC should be equal to the earliest start time of time B. therefore, there are: activity_early[BC] = event_early[B]
event : A B C D E F G H I
event_early : 0 6 4 5 7 7 16 14 18
event_latest: 0 6 6 8 7 10 16 14 18
activity : AB AC AD BE CE DF EG EH FH GI HI
activity_early : 0 0 0 6 4 5 7 7 7 16 14
(4) activity_latest analysis
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-tybgs2yh-1642157321023) (data: image / GIF; Base64, r0lgodlhaqabaabapap / / / waaach5baekaaaaaaaaaaabaaaeaaaicraeaow = =)]
activity_ The latest is calculated after going
For example, the latest start time of the activity CD should ensure that the latest time of time D cannot be delayed: activity_latest[CD] = event_latest[D] - len[CD]
event : A B C D E F G H I
event_early : 0 6 4 5 7 7 16 14 18
event_latest: 0 6 6 8 7 10 16 14 18
activity : AB AC AD BE CE DF EG EH FH GI HI
activity_early : 0 0 0 6 4 5 7 7 7 16 14
activity_latest: 0 2 3 6 6 8 7 11 10 16 14
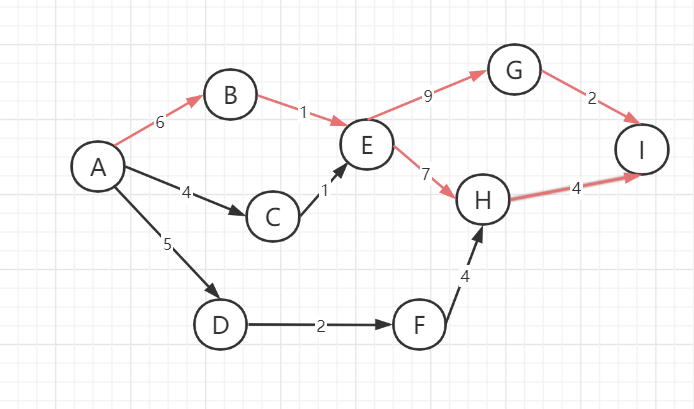
Key activities:
The earliest start time and the latest start time are the same, which are called key activities.
activity : AB AC AD BE CE DF EG EH FH GI HI
activity_early : 0 0 0 6 4 5 7 7 7 16 14
activity_latest: 0 2 3 6 6 8 7 7 10 16 14
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-9qtf4guo-1642157321023) (data: image / GIF; Base64, r0lgodlhaqabapabap / / / wuaaach5baekaaaaaaaaaaabaaaeaaaicraeaow = =)]
- The path composed of key activities is called critical path
- Although multiple critical paths will be generated, the execution time of multiple critical paths is the same.
- The total execution time of the project is the total execution time of any one of the critical paths.
6, Animation demonstration
https://www.bilibili.com/video/BV1PW41187vc
7, Code implementation
aoe.go
package aoe
import (
"fmt"
"gitee.com/gudongkun/datestruct/dataStructures/graph"
"gitee.com/gudongkun/datestruct/dataStructures/linear"
)
func GetGraph() graph.DMGraph {
g := graph.NewDMGraph()
g.AddNode("A")
g.AddNode("B")
g.AddNode("C")
g.AddNode("D")
g.AddNode("E")
g.AddNode("F")
g.AddNode("G")
g.AddNode("H")
g.AddNode("I")
g.AddEdge("A", "B", 6)
g.AddEdge("A", "C", 4)
g.AddEdge("A", "D", 5)
g.AddEdge("B", "E", 1)
g.AddEdge("C", "E", 1)
g.AddEdge("E", "G", 9)
g.AddEdge("E", "H", 7)
g.AddEdge("G", "I", 2)
g.AddEdge("H", "I", 4)
g.AddEdge("D", "F", 2)
g.AddEdge("F", "H", 4)
return g
}
func AOEKeyEvents() []string {
g := GetGraph()
eventEarly := make(map[string]int)
eventLatest := make(map[string]int)
activeEarly := make(map[string]int)
activeLatest := make(map[string]int)
// 1. Ask eventEarly
indegrees := make(map[string]int)
stack := linear.NewStack()
for _, v := range g.Nodes {
indegrees[v] = g.GetIndegree(v)
if indegrees[v] == 0 {
stack.Push(v)
indegrees[v] = -1
eventEarly[v] = 0
}
}
for !stack.IsEmpty() {
v, _ := stack.Pop()
for _, edge := range g.GetEdgesByHead(v) {
indegrees[edge.Tail]--
if indegrees[edge.Tail] == 0 {
stack.Push(edge.Tail)
indegrees[edge.Tail] = -1
for _, endEdge := range g.GetEdgesByTail(edge.Tail) {
val, ok := eventEarly[edge.Tail]
if !ok {
eventEarly[edge.Tail] = eventEarly[endEdge.Head] + endEdge.Val
} else {
if val < eventEarly[endEdge.Head]+endEdge.Val {
eventEarly[edge.Tail] = val
}
}
}
}
}
}
// 2. Find eventLatest
outdegrees := make(map[string]int)
outstack := linear.NewStack()
for _, v := range g.Nodes {
outdegrees[v] = g.GetOutdegree(v)
if outdegrees[v] == 0 {
outstack.Push(v)
outdegrees[v] = -1
eventLatest[v] = eventEarly[v]
}
}
for !outstack.IsEmpty() {
v, _ := outstack.Pop()
for _, edge := range g.GetEdgesByTail(v) {
outdegrees[edge.Head]--
if outdegrees[edge.Head] == 0 {
outstack.Push(edge.Head)
outdegrees[edge.Head] = -1
for _, endEdge := range g.GetEdgesByHead(edge.Head) {
val, ok := eventLatest[edge.Head]
if !ok {
eventLatest[edge.Head] = eventLatest[endEdge.Tail] - endEdge.Val
} else {
if val < eventLatest[endEdge.Tail]-endEdge.Val {
eventLatest[edge.Head] = val
}
}
}
}
}
}
// 3. Ask for activityEarly
for _, v := range g.GetEdgeList() {
activeEarly[v.Head+"-"+v.Tail] = eventEarly[v.Head]
}
// 4. Find activeLatest
for _, v := range g.GetEdgeList() {
activeLatest[v.Head+"-"+v.Tail] = eventLatest[v.Tail] - v.Val
}
// 5. Key activities
var keyActivity []string
for k,v := range activeEarly {
if activeLatest[k] == v {
keyActivity = append(keyActivity,k)
}
}
fmt.Println(keyActivity)
return keyActivity
}
aoe_test.go
package aoe
import "testing"
func TestAOEKeyEvents(t *testing.T) {
list := AOEKeyEvents()
if len(list) != 6 {
t.Fail()
}
}
Dmgraph with new method added go
package graph
import (
"errors"
)
const DMaxSize = 20
const DMaxNum = 99999
type DMGraph struct {
Edges [DMaxSize][DMaxSize]int
EdgeNum int
Nodes []string
Indexs map[string]int
}
type DEdge struct {
Head, Tail string
Val int
}
func NewDMGraph() DMGraph {
var g DMGraph
for k, v := range g.Edges {
for kk, _ := range v {
if k == kk {
g.Edges[k][kk] = 0
} else {
g.Edges[k][kk] = DMaxNum
}
}
}
g.Indexs = make(map[string]int)
return g
}
func (g *DMGraph) AddNode(nodeName string) error {
if g.Indexs == nil {
return errors.New("Is not a valid graph")
}
if _, ok := g.Indexs[nodeName]; ok {
return errors.New("This node has been added")
}
g.Indexs[nodeName] = len(g.Nodes)
g.Nodes = append(g.Nodes, nodeName)
return nil
}
func (g *DMGraph) AddEdge(Head, Tail string, val int) error {
if _, ok := g.Indexs[Head]; !ok {
return errors.New("Node does not exist:" + Head)
}
if _, ok := g.Indexs[Tail]; !ok {
return errors.New("Node does not exist:" + Tail)
}
if g.Edges[g.Indexs[Head]][g.Indexs[Tail]] != DMaxNum {
return errors.New("Edge already exists")
}
g.Edges[g.Indexs[Head]][g.Indexs[Tail]] = val
g.EdgeNum++
return nil
}
func (g *DMGraph) GetEdgeList() []DEdge {
var edgeList []DEdge
for i := 0; i < len(g.Nodes); i++ {
for j := 0; j < len(g.Nodes); j++ {
if g.Edges[i][j] != DMaxNum && i != j {
edgeList = append(
edgeList,
DEdge{Head: g.Nodes[i], Tail: g.Nodes[j], Val: g.Edges[i][j]},
)
}
}
}
return edgeList
}
func (g *DMGraph) GetIndegree(ele string) int {
tail, ok := g.Indexs[ele]
if !ok {
return -1 //Point does not exist
}
indegree := 0
for i := 0; i < len(g.Nodes); i++ {
if g.Edges[i][tail] != 0 && g.Edges[i][tail] != DMaxNum {
indegree++
}
}
return indegree
}
func (g *DMGraph) GetOutdegree(ele string) int {
head, ok := g.Indexs[ele]
if !ok {
return -1 //Point does not exist
}
outdegree := 0
for i := 0; i < len(g.Nodes); i++ {
if g.Edges[head][i] != 0 && g.Edges[head][i] != DMaxNum {
outdegree++
}
}
return outdegree
}
func (g *DMGraph) GetEdgesByTail(ele string) []DEdge {
var edgeList []DEdge
tail, ok := g.Indexs[ele]
if !ok {
return nil
}
for i := 0; i < len(g.Nodes); i++ {
if g.Edges[i][tail] != 0 && g.Edges[i][tail] != DMaxNum {
edgeList = append(
edgeList,
DEdge{Head: g.Nodes[i], Tail: g.Nodes[tail], Val: g.Edges[i][tail]},
)
}
}
return edgeList
}
func (g *DMGraph) GetEdgesByHead(ele string) []DEdge {
var edgeList []DEdge
head, ok := g.Indexs[ele]
if !ok {
return nil
}
for i := 0; i < len(g.Nodes); i++ {
if g.Edges[head][i] != 0 && g.Edges[head][i] != DMaxNum {
edgeList = append(
edgeList,
DEdge{Head: g.Nodes[head], Tail: g.Nodes[i], Val: g.Edges[head][i]},
)
}
}
return edgeList
}