RSA

RSA encryption takes advantage of the simple forward solution and complex reverse solution of one-way function

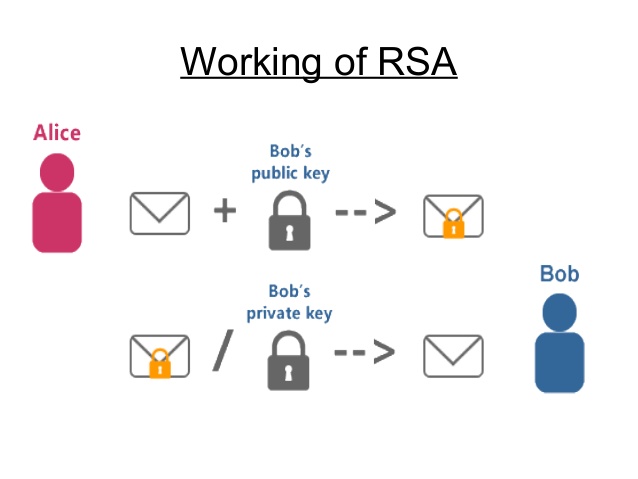
Basic concepts

1, What is "prime"?
A prime number is an integer that cannot be expressed as the product of any other two integers except that it can be expressed as the product of itself and 1. For example, 15 = 3 * 5, so 15 is not a prime number; For another example, 12 = 6 * 2 = 4 * 3, so 12 is not a prime. On the other hand, 13 cannot be expressed as the product of any other two integers except that it is equal to 13 * 1, so 13 is a prime number. Prime numbers are also called prime numbers.

2, What is coprime (or coprime)?
The definition of Coprime number in primary school mathematics textbooks is as follows: "two numbers with only 1 common divisor are called coprime numbers." The "two numbers" mentioned here refer to natural numbers.
The discrimination methods mainly include the following (not limited to):
(1) Two prime numbers must be coprime numbers. For example, 2 and 7, 13 and 19.
(2) If a prime number cannot be divided by another composite number, the two numbers are coprime numbers. For example, 3 and 10, 5 and 26.
(3) 1 is neither a prime number nor a composite number. It is a coprime number together with any natural number. Such as 1 and 9908.
(4) Two adjacent natural numbers are coprime. Such as 15 and 16.
(5) Two adjacent odd numbers are coprime numbers. Such as 49 and 51.
(6) Large numbers are prime numbers, and two numbers are coprime numbers. Such as 97 and 88.
(7) Decimals are prime numbers, and large numbers are not multiples of decimals. Two numbers are coprime numbers. Such as 7 and 16.
(8) Both numbers are composite numbers (the difference between two numbers is large). All the prime factors of decimals are not divisors of large numbers. These two numbers are coprime numbers. For example, 357 and 715357 = 3 × seven × 17, while 3, 7 and 17 are not divisors of 715. These two numbers are coprime numbers. wait.

3, What is modular exponential operation?
Everyone knows exponential operation. Needless to say, let's talk about modular operation first. Modular operation is an integer operation. There is an integer m, which takes n as the module for modular operation, that is, m mod n. How? Let m be divided by N and take only the remainder as the result, which is called modular operation. For example, 10 mod 3=1; 26 mod 6=2； 28 mod 2 =0, etc.
Modular exponential operation is to do exponential operation first, take the result and then do modular operation. For example, (5^3) mod 7 = (125 mod 7) = 6.

RSA encryption and decryption

RSA is an important application of public key encryption algorithm. RSA encryption algorithm consists of five parts:

• Message: the information that needs to be encrypted, which can be digital, text, video, audio, etc M M M indicates.
• Ciphertext: information obtained after encryption, using C C C means.
• Public key and secret key P K PK PK and S K SK SK indicates.
• Encryption algorithm: if E ( x ) E(x) E(x) is an encryption algorithm, and the encryption process can be understood as C = E ( M ) C = E(M) C=E(M) get the ciphertext according to the original text and encryption algorithm.
• Decryption algorithm: if D ( x ) D(x) D(x) is the decryption algorithm, and the decryption process can be understood as M = D ( C ) M = D(C) M=D(C) get the original text according to the ciphertext and decryption algorithm.

Suppose Alice and Bob want to encrypt communication on the Internet, how do they apply RSA to encrypt and decrypt information? The steps are as follows:

1. Randomly select two different prime numbers p , q p,q p,q .
2. take p , q p,q p. Multiply Q and write it as n = p × q n = p\times q n=p×q .
3. calculation n n Euler function of n φ ( n ) \varphi(n) φ (n) When the Euler function is proved p , q p,q p. When q is a different prime, φ ( n ) = ( p − 1 ) ( q − 1 ) \varphi(n)=(p-1)(q-1) φ(n)=(p−1)(q−1) .
4. Select an integer at random e e e. Two conditions are met: φ ( n ) \varphi(n) φ (n) And e e e coprime, and 1 < e < φ ( n ) 1<e<\varphi(n) 1<e<φ(n) .
5. calculation e e e for φ ( n ) \varphi(n) φ (n) Modular inverse element of d d d. That means finding one d d d meet e d = 1 m o d φ ( n ) ed = 1 mod\varphi(n) ed=1mod φ (n). This formula is equivalent to e d − 1 = k φ ( n ) ed-1 = k\varphi(n) ed−1=k φ (n) So, it's actually for the equation e d − k φ ( n ) = 1 ed-k\varphi(n) = 1 ed−k φ (n)=1 ( d , k ) (d,k) (d,k). This equation can be solved by extended Euclidean algorithm.
6. Finally ( e , n ) (e,n) (e,n) encapsulated as a public key, ( d , n ) (d,n) (d,n) encapsulated as a private key.

Let's run this algorithm through a practical example.

RSA algorithm

Java version

package com.tencent.blue.utils;

import org.apache.tomcat.util.codec.binary.Base64;
import org.apache.tomcat.util.http.fileupload.IOUtils;

import javax.crypto.Cipher;
import java.io.ByteArrayOutputStream;
import java.security.*;
import java.security.interfaces.RSAPrivateKey;
import java.security.interfaces.RSAPublicKey;
import java.security.spec.InvalidKeySpecException;
import java.security.spec.PKCS8EncodedKeySpec;
import java.security.spec.X509EncodedKeySpec;
import java.util.HashMap;
import java.util.Map;

/**
 * Created by cuiran on 19/1/9.
 */
public class RSAUtils {

    public static final String CHARSET = "UTF-8";
    public static final String RSA_ALGORITHM = "RSA";


    public static Map<String, String> createKeys(int keySize){
        //Create a KeyPairGenerator object for the RSA algorithm
        KeyPairGenerator kpg;
        try{
            kpg = KeyPairGenerator.getInstance(RSA_ALGORITHM);
        }catch(NoSuchAlgorithmException e){
            throw new IllegalArgumentException("No such algorithm-->[" + RSA_ALGORITHM + "]");
        }

        //Initialize KeyPairGenerator object, key length
        kpg.initialize(keySize);
        //Generate key pair
        KeyPair keyPair = kpg.generateKeyPair();
        //Get public key
        Key publicKey = keyPair.getPublic();
        String publicKeyStr = Base64.encodeBase64URLSafeString(publicKey.getEncoded());
        //Get private key
        Key privateKey = keyPair.getPrivate();
        String privateKeyStr = Base64.encodeBase64URLSafeString(privateKey.getEncoded());
        Map<String, String> keyPairMap = new HashMap<String, String>();
        keyPairMap.put("publicKey", publicKeyStr);
        keyPairMap.put("privateKey", privateKeyStr);

        return keyPairMap;
    }

    /**
     * Get public key
     * @param publicKey Key string (base64 encoded)
     * @throws Exception
     */
    public static RSAPublicKey getPublicKey(String publicKey) throws NoSuchAlgorithmException, InvalidKeySpecException {
        //Obtain the public Key object through the Key instruction encoded by X509
        KeyFactory keyFactory = KeyFactory.getInstance(RSA_ALGORITHM);
        X509EncodedKeySpec x509KeySpec = new X509EncodedKeySpec(Base64.decodeBase64(publicKey));
        RSAPublicKey key = (RSAPublicKey) keyFactory.generatePublic(x509KeySpec);
        return key;
    }

    /**
     * Get private key
     * @param privateKey Key string (base64 encoded)
     * @throws Exception
     */
    public static RSAPrivateKey getPrivateKey(String privateKey) throws NoSuchAlgorithmException, InvalidKeySpecException {
        //Obtain the private Key object through the PKCS#8 encoded Key instruction
        KeyFactory keyFactory = KeyFactory.getInstance(RSA_ALGORITHM);
        PKCS8EncodedKeySpec pkcs8KeySpec = new PKCS8EncodedKeySpec(Base64.decodeBase64(privateKey));
        RSAPrivateKey key = (RSAPrivateKey) keyFactory.generatePrivate(pkcs8KeySpec);
        return key;
    }

    /**
     * Public key encryption
     * @param data
     * @param publicKey
     * @return
     */
    public static String publicEncrypt(String data, RSAPublicKey publicKey){
        try{
            Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
            cipher.init(Cipher.ENCRYPT_MODE, publicKey);
            return Base64.encodeBase64URLSafeString(rsaSplitCodec(cipher, Cipher.ENCRYPT_MODE, data.getBytes(CHARSET), publicKey.getModulus().bitLength()));
        }catch(Exception e){
            throw new RuntimeException("Encrypted string[" + data + "]Exception encountered while", e);
        }
    }

    /**
     * Private key decryption
     * @param data
     * @param privateKey
     * @return
     */

    public static String privateDecrypt(String data, RSAPrivateKey privateKey){
        try{
            Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
            cipher.init(Cipher.DECRYPT_MODE, privateKey);
            return new String(rsaSplitCodec(cipher, Cipher.DECRYPT_MODE, Base64.decodeBase64(data), privateKey.getModulus().bitLength()), CHARSET);
        }catch(Exception e){
            throw new RuntimeException("Decrypt string[" + data + "]Exception encountered while", e);
        }
    }

    /**
     * Private key encryption
     * @param data
     * @param privateKey
     * @return
     */

    public static String privateEncrypt(String data, RSAPrivateKey privateKey){
        try{
            Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
            cipher.init(Cipher.ENCRYPT_MODE, privateKey);
            return Base64.encodeBase64URLSafeString(rsaSplitCodec(cipher, Cipher.ENCRYPT_MODE, data.getBytes(CHARSET), privateKey.getModulus().bitLength()));
        }catch(Exception e){
            throw new RuntimeException("Encrypted string[" + data + "]Exception encountered while", e);
        }
    }

    /**
     * Public key decryption
     * @param data
     * @param publicKey
     * @return
     */

    public static String publicDecrypt(String data, RSAPublicKey publicKey){
        try{
            Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
            cipher.init(Cipher.DECRYPT_MODE, publicKey);
            return new String(rsaSplitCodec(cipher, Cipher.DECRYPT_MODE, Base64.decodeBase64(data), publicKey.getModulus().bitLength()), CHARSET);
        }catch(Exception e){
            throw new RuntimeException("Decrypt string[" + data + "]Exception encountered while", e);
        }
    }

    private static byte[] rsaSplitCodec(Cipher cipher, int opmode, byte[] datas, int keySize){
        int maxBlock = 0;
        if(opmode == Cipher.DECRYPT_MODE){
            maxBlock = keySize / 8;
        }else{
            maxBlock = keySize / 8 - 11;
        }
        ByteArrayOutputStream
                out = new ByteArrayOutputStream();
        int offSet = 0;
        byte[] buff;
        int i = 0;
        try{
            while(datas.length > offSet){
                if(datas.length-offSet > maxBlock){
                    buff = cipher.doFinal(datas, offSet, maxBlock);
                }else{
                    buff = cipher.doFinal(datas, offSet, datas.length-offSet);
                }
                out.write(buff, 0, buff.length);
                i++;
                offSet = i * maxBlock;
            }
        }catch(Exception e){
            throw new RuntimeException("The encryption and decryption threshold is["+maxBlock+"]An exception occurred while retrieving data for", e);
        }
        byte[] resultDatas = out.toByteArray();
        IOUtils.closeQuietly(out);
        return resultDatas;
    }

    public static void main (String[] args) throws Exception {
        Map<String, String> keyMap = RSAUtils.createKeys(1024);
        String  publicKey = keyMap.get("publicKey");
        String  privateKey = keyMap.get("privateKey");
        System.out.println("Public key: \n\r" + publicKey);
        System.out.println("Private key: \n\r" + privateKey);

        System.out.println("Public key encryption - private key decryption");
        String str = "code_cayden";
        System.out.println("\r Plaintext:\r\n" + str);
        System.out.println("\r Plaintext size:\r\n" + str.getBytes().length);
        String encodedData = RSAUtils.publicEncrypt(str, RSAUtils.getPublicKey(publicKey));
        System.out.println("Ciphertext:\r\n" + encodedData);
        String decodedData = RSAUtils.privateDecrypt(encodedData, RSAUtils.getPrivateKey(privateKey));
        System.out.println("Decrypted text: \r\n" + decodedData);


    }


}

C++

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include<string.h>
#include <math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
int e, d, n;

int gcd(int a, int b)  //greatest common factor 
{
    int c = 0;
    if(a<b) swap(a,b);
    c = b;
    do
    {
        b = c;
        c = a%b;
        a = b;
    }
    while (c != 0);
    return b;
}

int PrimarityTest(int a, int i) //Judge whether i is prime
{
    int flag=0;
    for(a;a<i;a++)
    {
        if(i%a==0)
        {
            flag=1;
            break;
        }
    }
    if(flag) return 0;
    return 1;
    // complete this part
}

int ModularExponention(int a, int b, int n)  //Find a^bmodn
{
    int y;

    /*Calculate pow (a, b)% n using binary square multiplication*/
    y=1;

    while(b != 0)
    {
        /*For each 1 in b, accumulate y*/

        if(b & 1)
            y = (y*a) % n;

        /*For each bit in b, calculate the square of a*/
        a = (a*a) % n;

        /*Prepare the next person in b*/
        b = b>>1;
    }

    return y;
    // complete this part
}

void extgcd(ll a,ll b,ll& d,ll& x,ll& y) //Get the result of (1/a)modb
{
    if(!b)
    {
        d=a;
        x=1;
        y=0;
    }
    else
    {
        extgcd(b,a%b,d,y,x);
        y-=x*(a/b);
    }
}

int ModularInverse(int a,int b)  //Get the result of (1/a)modb
{
    ll d,x,y;
    extgcd(a,b,d,x,y);
    return d==1?(x+b)%b:-1;
    // complete this part
}

void KeyGeneration()  //Get public key
{
    int p, q;
    int phi_n;

    do
    {
        do
            p = rand();
        while (p % 2 == 0);

    }
    while (!PrimarityTest(2, p));

    do
    {
        do
            q = rand();
        while (q % 2 == 0);
    }
    while (!PrimarityTest(2, q));

    n = p * q;
    phi_n = (p - 1) * (q - 1);

    do
        e = rand() % (phi_n - 2) + 2; // 1 < e < phi_n
    while (gcd(e, phi_n) != 1);

    d = ModularInverse(e,phi_n);
}

void Encryption(int value, FILE* out)  //encryption
{
    int cipher;
    cipher = ModularExponention(value, e, n);
    fprintf(out, "%d ", cipher);
}

void Decryption(int value, FILE* out)  //decrypt
{
    int decipher;
    decipher = ModularExponention(value, d, n);
    fprintf(out, "%c", decipher);
}
int main(void)
{
    FILE* inp, * out;
    char filepath[15], filename[100];

    strcpy(filepath, "F:\Desktop\\");  //File path

    sprintf(filename, "%s%s", filepath, "cipher.txt");
    out = fopen(filename, "w+");  //Open file
    fclose(out);
    sprintf(filename, "%s%s", filepath, "decipher.txt");
    out = fopen(filename, "w+");  //Open file
    fclose(out);

    KeyGeneration();  //Get public key

    sprintf(filename, "%s%s", filepath, "plain.txt");
    inp = fopen(filename, "r+");  //Read original file
    if (inp == NULL)
    {
        printf("Error opening Source File.\n");
        exit(1);
    }

    sprintf(filename, "%s%s", filepath, "cipher.txt");
    out = fopen(filename, "w+");
    if (out == NULL)
    {
        printf("Error opening Destination File.\n");
        exit(1);
    }

    // encryption starts
    while (1)
    {
        char ch = getc(inp);  //Read file characters, read and output one character by one
        if (ch == -1)
            break;
        int value = toascii(ch);  //toascii converts characters into corresponding ascall values
        Encryption(value, out);  //Encrypted output
    }

    fclose(inp);
    fclose(out);

    // decryption starts
    sprintf(filename, "%s%s", filepath, "cipher.txt");
    inp = fopen(filename, "r");
    if (inp == NULL)
    {
        printf("Error opening Cipher Text.\n");
        exit(1);
    }

    sprintf(filename, "%s%s", filepath, "decipher.txt");
    out = fopen(filename, "w+");
    if (out == NULL)
    {
        printf("Error opening File.\n");
        exit(1);
    }

    while (1)
    {
        int cip;
        if (fscanf(inp, "%d", &cip) == -1)
            break;
        Decryption(cip, out);  //decrypt
    }
    fclose(out);

    return 0;
}

Why do passwords have to use prime numbers?

Who can answer this question?