cs61b experimental record (VI) HW4 A* search algorithm
Specifically, given an object of type WorldState, our solver will take that WorldState and find a sequence of valid transitions between world states such that the puzzle is solved.
all puzzles will be implementations of the WorldState interface, given below
public interface WorldState {
/** Provides an estimate of the number of moves to reach the goal.
* Must be less than or equal to the correct distance. */
int estimatedDistanceToGoal();
/** Provides an iterable of all the neighbors of this WorldState. */
Iterable<WorldState> neighbors();
/** Estimates the distance to the goal. Must be less than or equal
* to the actual (and unknown) distance. */
default public boolean isGoal() {
return estimatedDistanceToGoal() == 0;
}
}
every WorldState object must be able to
- return all of its neighbors
- it must have a method to return the estimated distance to the goal and this estimate must be less than or equal to the true distance
Suppose that the current WorldState is the starting word "horse", and our goal is to get to the word "nurse". In this case,
- Neighbors () would return ["house", "word", "house", "horses"], neighbor s are all states that can be reached with only one operation.
- estimatedDistanceToGoal might return 2, since changing ‘h’ into ‘n’, and ‘o’ into ‘u’ would result in reaching the goal. Just check how many characters are inconsistent between the start word and the target word. The result must be less than or equal to the number of operations required to convert to the target character.
A* search algorithm
We need to define the search unit in the puzzle. The SearchNode class has the following attributes:
- WorldState
- The number of operations required from the initial state to the current state
- A reference to the last state
The process of best first search algorithm is as follows:
- We need to maintain a queue. The content of the queue is the SearchNode object to obtain the best movement state from the queue
- Remove the best move state from the queue
- If the state is the target state, then the end
- If this state is not the target state, take this state as the center, get its neighbor, create SearchNode objects, and add them to the queue
- Then get the best state from the queue, and so on
The priority comparison mechanism of the queue is as follows: the priority of each SearchNode object is equal to the sum of the number of operations from the starting state to the current state and the estimated number of operations from the current state to the target state.
The A* algorithm can also be thought of as "Given a state, pick a neighbor state such that (distance so far + estimated distance to goal) is minimized. Repeat until the goal is seen"
To see an example of this algorithm in action, see this video or these slides.
Solver
Optimizations
Searchnodes corresponding to the same state may be added to the queue many times. Therefore, in order to avoid repeatedly adding and exploring the same state, we need to mark all the passed states. be careful! "Past state" refers to the state that once took this state as the center and added its neighbor to the queue, that is, the state that has been out of the queue! Instead of having joined the team, but not having explored around with it as the center! Its principle is the same as that of Dijkstra. There is more than one way to this state. We have only explored one of them. At this time, we are not sure whether this road is the shortest. Marking this state means that the road leading to it has been determined, and other roads can no longer lead to this state. Only through the next exit of the priority queue can we judge which way is the shortest at this time. After leaving the queue, it means that this point is the closest point to the end point determined by the priority queue. At this point, we can mark this point, indicating that we don't need to explore this point any more.
Marking method: all passed states can be marked (the method adopted by Dijkstra). In this example, the method is to add a previous attribute in SearchNode to refer to the previous node. You only need to avoid adding your parent node to the queue.
A second optimization:
To avoid recomputing the estimatedDistanceToGoal() result from scratch each time during various priority queue operations, compute it at most once per object; save its value in an instance variable;
implementation
SearchNode:
public class SearchNode implements Comparable<SearchNode>{
public WorldState word;
public int moves;
public SearchNode previous;
public int priority;
public SearchNode(WorldState w,int m,SearchNode p){
word=w;
moves=m;
previous=p;
priority=moves+w.estimatedDistanceToGoal();
}
@Override
public int compareTo(SearchNode o) {
return this.priority-o.priority;
}
}
Solver:
-
a naive way:
public class Solver { private int moves=0; private MinPQ<SearchNode>MP=new MinPQ<>(); private ArrayList<WorldState>solutions=new ArrayList<>(); public Solver(WorldState initial){ MP.insert(new SearchNode(initial,0,null)); while (!MP.min().word.isGoal()){ //Each time you explore around a point, increase the number of steps by one moves++; SearchNode min=MP.min(); for (WorldState w:min.word.neighbors()){ //If the currently detected neighbor is different from its parent node, you can join the queue if (min.previous==null||!w.equals(min.previous.word)){ MP.insert(new SearchNode(w, moves,min)); } } solutions.add(min.word); MP.delMin(); } solutions.add(MP.min().word); } public int moves(){ return moves; } public Iterable<WorldState> solution() { return solutions; } }In the above method, I made a fatal mistake. I marked every point exploring outward with it as moves + +, but this is not the actual number of moves of the point. What we need to find is the shortest path to the target state. The real number of movements of a point should be the direct distance from the starting point to that point. I mistakenly think that I can go down a road from the starting point to the target point and never look back until the target point. However, similar to Dijkstra and Prim, we always choose the best path in the priority queue. We may go back on one road and choose another.
For example, from horse - > nurse, we can separate [horse 4, worse 3, horses 4] from horse. At this time, we should select worse to exclude horse from the queue. We can separate [worst 5] from worse. Obviously, at this time, we need to go back and select hose or horses. However, if I follow the above practice, if I choose choose choose at this time, its number of moves will become 2 (horse - > worse - > horse), but its actual number of moves should be 1 (horse - > horse). Therefore, you should not use moves + + every time you explore a point. The moves of all SearchNode objects should be based on the moves+1 of its parent node (similar to the operation of DFS and BFS to calculate the path length).
Similarly, the final specific path should start from the end point and trace upward along the parent node of each point to the starting point.
-
The right approach:
public class Solver { private MinPQ<SearchNode>MP=new MinPQ<>(); private ArrayList<WorldState>solutions=new ArrayList<>(); public Solver(WorldState initial){ MP.insert(new SearchNode(initial,0,null)); while (!MP.min().word.isGoal()){ SearchNode min=MP.delMin(); for (WorldState w:min.word.neighbors()) //If the currently detected neighbor is different from its parent node, you can join the queue if (min.previous==null||!w.equals(min.previous.word)) MP.insert(new SearchNode(w, min.moves+1,min)); } } public int moves(){ return MP.min().moves; } public Iterable<WorldState> solution() { Stack<WorldState>stack=new Stack<>(); SearchNode pos=MP.min(); while (pos!=null) { stack.push(pos.word); pos=pos.previous; } while (!stack.isEmpty()) solutions.add(stack.pop()); return solutions; } }BTW, this algorithm is really too slow. I waited for a long time without results. I thought it was a mistake in the algorithm, which made me look for a bug all day. Finally, I found it was right, but it was too slow
Board
Goal Distance Estimates
We consider two goal distance estimates:
- Hamming estimate: The number of tiles in the wrong position.
- Manhattan estimate: The sum of the Manhattan distances (sum of the vertical and horizontal distance) from the tiles to their goal positions.
8 1 3 1 2 3 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 4 2 4 5 6 ---------------------- ---------------------- 7 6 5 7 8 1 1 0 0 1 1 0 1 1 2 0 0 2 2 0 3 initial goal Hamming = 5 + 0 Manhattan = 10 + 0
We can regard the process of A* search algorithm as a tree. Each state is one of its nodes, and its neighbor corresponds to its child nodes. Leaf nodes are in the priority queue, and all internal nodes have been processed and deleted from the priority queue. Each time, take a leaf node as the center to explore outward, delete the leaf node from the priority queue, and add the unprocessed node adjacent to it to the priority queue to become a new leaf node. The above process is basically similar to Prim and Dijkstra algorithms.
Board:
public class Board implements WorldState{
private int N;
private int[][]start;
private int[][]goal;
private static final int BLANK=0;
public Board(int[][] tiles){
N=tiles.length;
goal=new int[N][N];
start = new int[N][N];
int cnt=1;
for (int i=0;i<N;i++){
for (int j=0;j<N;j++){
goal[i][j]=cnt;
cnt++;
}
}
goal[N-1][N-1]=0;
for (int i=0;i<N;i++){
for (int j=0;j<N;j++){
start[i][j]=tiles[i][j];
}
}
}
public int tileAt(int i, int j){
if (i<0||j<0||i>=N||j>=N)
throw new IndexOutOfBoundsException("i and j must between 0 and N-1");
return start[i][j];
}
public int size(){
return N;
}
public int hamming(){
int hamming=0;
for (int i=0;i<N;i++){
for (int j=0;j<N;j++){
if (goal[i][j] != start[i][j] && goal[i][j] != BLANK) {
hamming++;
}
}
}
return hamming;
}
public int manhattan(){
int manhattan=0;
for (int i=0;i<N;i++){
for (int j=0;j<N;j++){
int number=start[i][j];
if (number!=BLANK){
int goalX = (number - 1) / N;
int goalY = (number - 1) % N;
manhattan += Math.abs(i - goalX) + Math.abs(j - goalY);
}
}
}
return manhattan;
}
public boolean equals(Object y){
if (y == this) return true;
if (y == null || y.getClass() != this.getClass()) return false;
Board a=(Board)y;
if (a.size()!=this.size()) return false;
for (int i=0;i<N;i++)
for (int j=0;j<N;j++)
if (a.tileAt(i,j)!=this.tileAt(i,j))
return false;
return true;
}
@Override
public int estimatedDistanceToGoal() {
return manhattan();
}
@Override
public Iterable<WorldState> neighbors() {
Queue<WorldState> neighbors = new Queue<>();
int hug = size();
int bug = -1;
int zug = -1;
for (int rug = 0; rug < hug; rug++) {
for (int tug = 0; tug < hug; tug++) {
if (tileAt(rug, tug) == BLANK) {
bug = rug;
zug = tug;
}
}
}
int[][] ili1li1 = new int[hug][hug];
for (int pug = 0; pug < hug; pug++) {
for (int yug = 0; yug < hug; yug++) {
ili1li1[pug][yug] = tileAt(pug, yug);
}
}
for (int l11il = 0; l11il < hug; l11il++) {
for (int lil1il1 = 0; lil1il1 < hug; lil1il1++) {
if (Math.abs(-bug + l11il) + Math.abs(lil1il1 - zug) - 1 == 0) {
ili1li1[bug][zug] = ili1li1[l11il][lil1il1];
ili1li1[l11il][lil1il1] = BLANK;
Board neighbor = new Board(ili1li1);
neighbors.enqueue(neighbor);
ili1li1[l11il][lil1il1] = ili1li1[bug][zug];
ili1li1[bug][zug] = BLANK;
}
}
}
return neighbors;
}
/** Returns the string representation of the board.
* Uncomment this method. */
public String toString() {
StringBuilder s = new StringBuilder();
int N = size();
s.append(N + "\n");
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
s.append(String.format("%2d ", tileAt(i,j)));
}
s.append("\n");
}
s.append("\n");
return s.toString();
}
@Override
public int hashCode() {
return 0;
}
}
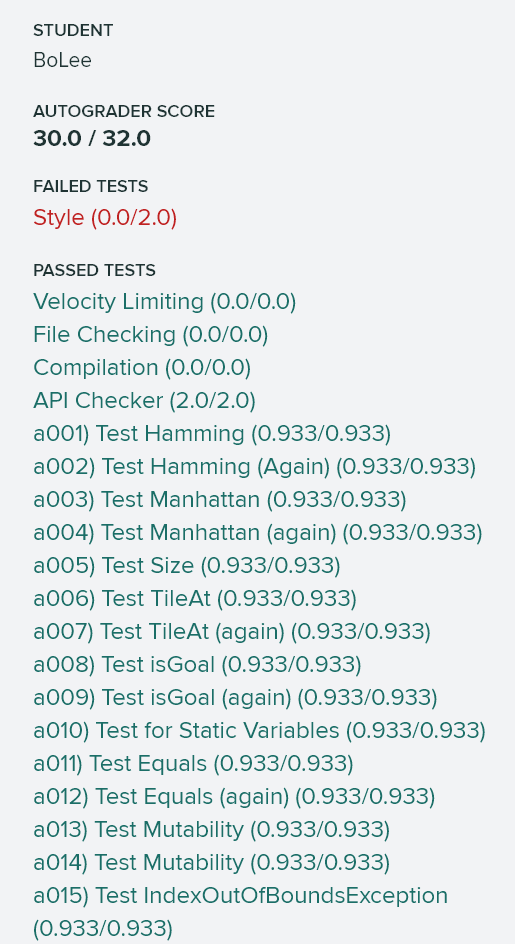
autograder rating: