- See you on the topic [CSP-J2020] expression - Luogu
- Knowledge point analysis:
- Be able to parse the specified data in the string. This topic requires to parse numbers and logical operators from the string. For ex amp le, x123 only resolves 123 and records it as the 123rd variable. For the convenience of storage, you can save &, |,! Save as a specified number, such as & save as - 1, | save as - 2,! Save into - 3, according to personal preferences. Such an array is sufficient.
- Master the suffix expression, and be able to calculate the value of the suffix expression by using the stack. Master the above two points, which can exceed 30pts
- Can establish suffix expression tree with stack, and query and maintain the root value of each subtree in the tree. 1. 3 two 95pts can be obtained. (the fourth point of the official data is a chain, so the time complexity changes from qlogn to q*n can not pass.)
- The characteristics of logical operation, namely a & B, a|b.
-
a
b
a&b
a|b
1
1
1
1
1
0
0
1
0
1
0
1
0
0
0
0
As can be seen from the above table, as long as one of a & B is 0, the result is 0, so it doesn't matter whether the other is 0 or not; a|b as long as one is 1, the result is 1, and the other doesn't matter. Therefore, many operands may be dispensable in the expression, that is, whether they exist or not does not affect the value of the expression at all. As in example 2, X2, X3, X4 and X5 are optional.
-
Therefore, from the knowledge of 3 and 4, we can draw a conclusion: the dispensable operands in the expression cannot change the final result of the expression, and those operands that must be able to change the final result of the expression. Therefore, through the traversal of the expression tree, the optional operands are marked. When changing an operand, as long as it is not a required operand, the initial value of the expression is returned directly. Otherwise, the initial value of the expression is reversed and returned. Time complexity n+p, 100pts
2, Code analysis:1, 30pts is pure violence. The result of each time is calculated by stack, and the time complexity is n*q (omitted)
2, 95pts uses the stack to build a tree. Each time the result is updated from the changed leaf node to the parent node, the tree root is the answer, and the time complexity is q*logn.
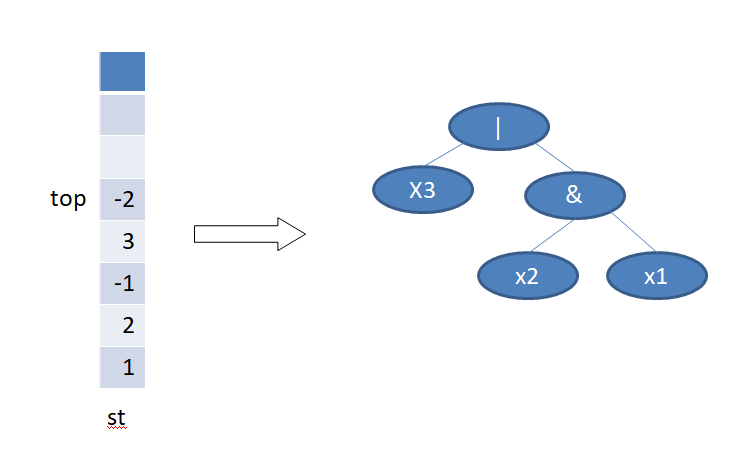
1. The value in the parsing expression is stored in the stack for standby. As in the ex amp le x1, X2 & x3 |, the operands are stored in numbers, and the operators & are stored in - 1, | - 2,! Save - 3, as shown in the right figure
2. Make achievements. Take the operand as the leaf node, the operator as the intermediate node, and the tree root is the last operator involved in the operation, that is, the last operator in the suffix expression, that is, the top element of the stack. The elements in the stack pop up in turn, return in case of operands, and recursively establish their left and right subtrees in case of operators. When the stack is empty, the tree is formed.
Read in the initial value of each operand and store it in the array:
| 1 | 0 | 1 |
Use structure array to store nodes and build the relationship between nodes.
Example 1 tree: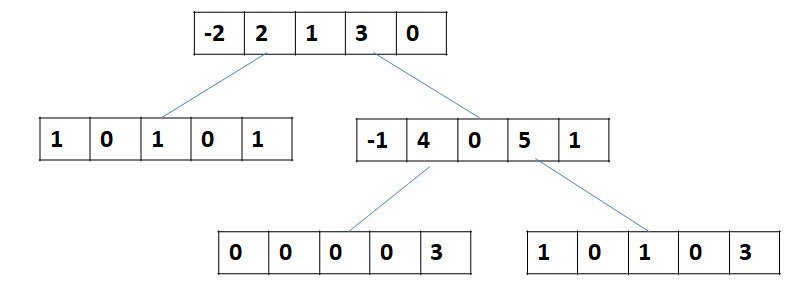
3. Read in the operand number to be modified. At this time, it should be noted that when building the tree, we should save the subscript of each operand in the structure array, so that when we read the operand number to be modified, we can directly find this node in the tree. For ex amp le, to modify the value of X2, the process: find the X2 node, set the current node as X2, find the parent node & of x2 through the tree structure, find another child node X1 through the parent node, and then replace the operation value of the parent node & with the result of operation x2 & x1. Then set the parent node as the current node and continue to look up until the root node. The operation value of the root node is the answer. Remember to restore the modified value (skillfully set recursive parameters without real modification, see the code) to complete a query.
Reference code:
#include<iostream>
#include<cstdio>
#include<string>
#define N 1000000
using namespace std;
struct NOD//Node of tree
{
int b;//Initial value
int lc,rc,pa;//About children and fathers
bool re;//The value of the tree with this node as the root
int f;//Firewood mark
};
struct NN//Record the initial value of n operands and the corresponding array subscript in the tree.
{
bool sn;//Record the initial value of the input operand
int p;//Subscript of record tree node in array
};
NN pos[N+10];
NOD a[N+10];//Tree building array
int p,cnt,n,q,st[N+10],top,v,u;//st is the array simulation stack to help build the tree. cnt is used to build the tree and record the total number of nodes. Top is the top mark of the stack and various temporary variables
int num; //Used to convert the subscript of the operand in the expression.
string s;//Save initial string
void init();//Parse the characters of the original expression, and store the results in the stack to prepare for tree building
void dfs(int k);//Calculate the result after changing a value.
void buildtree(int t);//Build a tree and calculate the value of each result when returning recursively.
int main()
{
init();
cin>>n;
for(int i=1;i<=n;i++)//Enter the initial value of n variables
scanf("%d",&pos[i].sn);
a[++cnt].b=st[top--];//Determine the root of the tree and store it at the subscript 1 of the array. Suffix expression, the last character is the tree root, which is the top element of the stack.
buildtree(1);//Start to build a tree with the subscript 1 of the tree group as the parent node
scanf("%d",&q);//Number of inquiries
while(q--)
{
scanf("%d",&u);
dfs(pos[u].p);//Bottom up calculation results
}
return 0;
}
void init()//There are various methods in the analysis process. It's good to achieve the goal
{
getline(cin,s);
int lts=s.length();
for(int i=0;i<lts;i++)
{
if(s[i]=='x')
{
i++;
num=0;
while(s[i]!=' ')
{
num=num*10+(s[i]-'0');i++;
}
st[++top]=num;//Operand subscript stack
}
else if(s[i]=='&')st[++top]=-1;//&Operator stack
else if(s[i]=='|')st[++top]=-2;//|Operator stack
else if(s[i]=='!')st[++top]=-3;//! Operator stack
}
}
void buildtree(int t)//Take the node with array subscript t as the tree root and try to establish its left and right subtrees
{
if(!a[t].lc)//If there is no left subtree, build the left subtree first
{
if(top<1)return;//When the stack is empty, no elements are available. The tree is established and returned.
v=st[top--];//Element out of stack into v
if(v>=0)//If it is 1 2 3 4... n, it is the operand
{
a[++cnt].b=pos[v].sn;//Save result initial value
a[cnt].re=a[cnt].b;//The result operation value is equal to the initial value
pos[v].p=cnt;//Record the position of the node in the tree
a[t].lc=cnt;//Left child marker
a[cnt].pa=t;//Father mark
//The operand is a leaf node without a subtree.....
}
else //If it is - 1, - 2, - 3, it is said to be an operator
{
a[++cnt].b=v;//Operators are saved directly to the tree
a[t].lc=cnt;//Left child marker
a[cnt].pa=t;//Father mark
buildtree(cnt);//Recursively establish a subtree of operators.
}
}
if(!a[t].rc&&a[t].b!=-3)//Create a right subtree. Note that if the root of the tree is a non operator, there is no right subtree. By default, one of its operands is built on the left subtree.
{
if(top<1)return;
v=st[top--];
if(v>=0)
{
a[++cnt].b=pos[v].sn;
a[cnt].re=a[cnt].b;
pos[v].p=cnt;
a[t].rc=cnt;
a[cnt].pa=t;
}
else
{
a[++cnt].b=v;
a[t].rc=cnt;
a[cnt].pa=t;
buildtree(cnt);
}
}
//Now that the left and right subtrees are established, calculate the value of the subtree below
if(a[t].b==-1)a[t].re=a[a[t].lc].re&a[a[t].rc].re;
else if(a[t].b==-2)a[t].re=a[a[t].lc].re|a[a[t].rc].re;
else if(a[t].b==-3)a[t].re=!a[a[t].lc].re;
}
void dfs(int k)//There are many ways to write the result after the change of the k operand of recursive query. You can complete the goal
{ //This way of writing is recursive only when k is sure to take the inverse.
if(k==1)
{
printf("%d\n",!a[1].re);
return;
}
bool b=!a[k].re;//The k-th number is reversed and stored in b, so the original result has not really changed, so it does not need to be reversed again after the query is completed
int pp=a[k].pa;//Save the corresponding father
int child;//The other child of the surviving father may be left or right
if(a[pp].b==-3)dfs(pp);//If the inverse operation is performed, it is directly recursive, because it can change the value of the parent node
else if(a[pp].b==-1)//If it is & operation, recursion can be performed only when the father can be changed
{
child=a[pp].lc==k?a[pp].rc:a[pp].lc;
if(a[child].re&b!=a[pp].re)dfs(pp);//If it is & operation, recursion can be performed only when the father can be changed
else //If the value of the parent node can no longer be changed, that is, it is determined to be fee ⒀. The value of the expression cannot be finally changed, and the value of the initial expression can be directly output
{
printf("%d\n",a[1].re);
return;
}
}
else if(a[pp].b==-2)//|Operation, class & operation
{
child=a[pp].lc==k?a[pp].rc:a[pp].lc;
if((a[child].re|b)!=a[pp].re)dfs(pp);
else
{
printf("%d\n",a[1].re);
return;
}
}
}
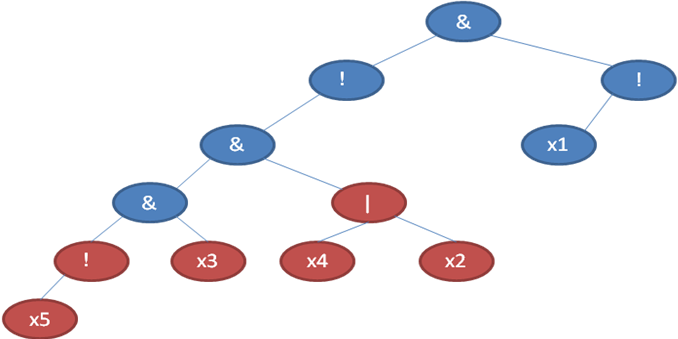
3, 100pts, which is optimized on the basis of 95pts. Using the analysis of knowledge points 4 and 5, mark the operand nodes that cannot affect the final value of the expression according to the initial value. The nodes that are not marked will certainly affect the final value when changing. Complete the O (1) change query. The total complexity O(n+q) is as shown in example 2. After marking, the following tree is displayed: Red nodes are useless nodes. For example 2, the red dot is useless. Only when the value of x1 is changed will it have an impact on the final result.
Reference code:
#include<iostream>
#include<cstdio>
#include<string>
#define N 1000000
using namespace std;
struct NOD//Node of tree
{
int b;//Initial value
int lc,rc,pa;//About children and fathers
bool re;//The value of the tree with this node as the root
int f;//Fei Chai mark
};
struct NN//Record the initial value of n operands and the corresponding array subscript in the tree.
{
bool sn;//Record the initial value of the input operand
int p;//Subscript of record tree node in array
};
NN pos[N+10];
NOD a[N+10];//Tree building array
int p,cnt,n,q,st[N+10],top,v,u;//st is the array simulation stack to help build the tree. cnt is used to build the tree and record the total number of nodes. Top is the top mark of the stack and various temporary variables
int num; //Used to convert the subscript of the operand in the expression.
string s;//Save initial string
void init();//Parse the characters of the original expression, and store the results in the stack to prepare for tree building
void fdfs(int k);//Firewood marking
void buildtree(int t);//Build a tree and calculate the value of each result when returning recursively.
int main()
{
init();
cin>>n;
for(int i=1;i<=n;i++)//Enter the initial value of n variables
scanf("%d",&pos[i].sn);
a[++cnt].b=st[top--];//Determine the root of the tree and store it at the subscript 1 of the array. Suffix expression, the last character is the tree root, which is the top element of the stack.
buildtree(1);//Start to build a tree with the subscript 1 of the tree group as the parent node
fdfs(1);//Recursion marks all the firewood on the tree.
scanf("%d",&q);//Number of inquiries
while(q--)
{
scanf("%d",&u);
if(a[pos[u].p].f==1)//If it is Fei Chai, the initial expression value is directly output
printf("%d\n",a[1].re);
else
//dfs(pos[u].p);
printf("%d\n",!a[1].re);//If it is not Fei Chai, take the inverse value of the initial expression and output it.
}
return 0;
}
void init()//There are various methods in the analysis process. It's good to achieve the goal
{
getline(cin,s);
int lts=s.length();
for(int i=0;i<lts;i++)
{
if(s[i]=='x')
{
i++;
num=0;
while(s[i]!=' ')
{
num=num*10+(s[i]-'0');i++;
}
st[++top]=num;//Operand subscript stack
}
else if(s[i]=='&')st[++top]=-1;//&Operator stack
else if(s[i]=='|')st[++top]=-2;//|Operator stack
else if(s[i]=='!')st[++top]=-3;//! Operator stack
}
}
void buildtree(int t)//Take the node with array subscript t as the tree root and try to establish its left and right subtrees
{
if(!a[t].lc)//If there is no left subtree, build the left subtree first
{
if(top<1)return;//When the stack is empty, no elements are available. The tree is established and returned.
v=st[top--];//Element out of stack into v
if(v>=0)//If it is 1 2 3 4... n, it is the operand
{
a[++cnt].b=pos[v].sn;//Save result initial value
a[cnt].re=a[cnt].b;//The result operation value is equal to the initial value
pos[v].p=cnt;//Record the position of the node in the tree
a[t].lc=cnt;//Left child marker
a[cnt].pa=t;//Father mark
//The operand is a leaf node without a subtree.....
}
else //If it is - 1, - 2, - 3, it is said to be an operator
{
a[++cnt].b=v;//Operators are saved directly to the tree
a[t].lc=cnt;//Left child marker
a[cnt].pa=t;//Father mark
buildtree(cnt);//Recursively establish a subtree of operators.
}
}
if(!a[t].rc&&a[t].b!=-3)//Create a right subtree. Note that if the root of the tree is a non operator, there is no right subtree. By default, one of its operands is built on the left subtree.
{
if(top<1)return;
v=st[top--];
if(v>=0)
{
a[++cnt].b=pos[v].sn;
a[cnt].re=a[cnt].b;
pos[v].p=cnt;
a[t].rc=cnt;
a[cnt].pa=t;
}
else
{
a[++cnt].b=v;
a[t].rc=cnt;
a[cnt].pa=t;
buildtree(cnt);
}
}
//Now that the left and right subtrees are established, calculate the value of the subtree below
if(a[t].b==-1)a[t].re=a[a[t].lc].re&a[a[t].rc].re;//Sum of operation values of left and right subtrees
else if(a[t].b==-2)a[t].re=a[a[t].lc].re|a[a[t].rc].re;//Summation of operation values of left and right subtrees
else if(a[t].b==-3)a[t].re=!a[a[t].lc].re;//If it is a non operation, we put its operand on the left subtree and directly take the value of the left subtree
}
void fdfs(int k)//Recursive marking. Traverse the whole number of subtrees with root k from top to bottom, and mark it if it is Fei Chai.
{
if(a[k].lc==0&&a[k].rc==0)return;//If k is a leaf, return directly
if(k!=1&&a[k].f==1) a[a[k].lc].f=a[a[k].rc].f=1;//If k-point is Fei Chai, all the children are Fei Chai
else//If k it's not Fei Chai, see if his children have Fei Chai
{
if(a[k].b==-1)//&Check whether one of the two children is 0. If one is 0, the other child is Fei Chai. If both are 0, they are Fei Chai
{
if(a[a[k].lc].re==0)a[a[k].rc].f=1;
if(a[a[k].rc].re==0)a[a[k].lc].f=1;
}
if(a[k].b==-2)//|Check whether one of the two children is 1. If one is 1, the other child is Fei Chai. If both are 1, they are Fei Chai.
{
if(a[a[k].lc].re==1)a[a[k].rc].f=1;
if(a[a[k].rc].re==1)a[a[k].lc].f=1;
}
}
fdfs(a[k].lc);//Recursive left subtree
fdfs(a[k].rc);//Recursive right subtree
}Summary:
- The data scale of this question is 10 ^ 6, and the maximum number of queries per test point is also 10 ^ 6. Therefore, the time complexity of n^2 can not solve this question. The average time of data processing for each query should not be higher than N, otherwise it will not pass. Therefore, it can be predicted that there must be a data preprocessing process once and for all. So I think of the time complexity solution of qlogn or q+n.
- Most of the problems related to expressions need to use data structures such as stack and binary tree. The processing time of tree is logn, so using tree to solve similar problems is the first thinking direction.