Dafeng Armored Air Mother
Time limit: 1 Sec memory limit: 128 MB
Submitted: 108 Solutions: 15
[Submission] [Status] [Proposer: admin]
Topic Description
The aircraft carrier Dafeng likes arithmetic very much.
It is the most advanced aircraft carrier in the old Japanese navy.
It was the shortest-lived aircraft carrier in the old Japanese navy.
At the same time, she is the flattest aircraft carrier.
So many first...
Life two, life three, life three things...
Maybe that's why Dafeng likes arithmetic.
One day, she saw such a question:
order
Electrical exploration has found torpedoes from afar, and time is running out.

input
Two non-negative integers separated by spaces in a row are n and p, respectively.

output
One line represents the answer.

sample input
Duplicate sample data
5 97
sample output
11

Tips
Time limit: 1 Sec memory limit: 128 MB
Submitted: 108 Solutions: 15
[Submission] [Status] [Proposer: admin]
Topic Description
The aircraft carrier Dafeng likes arithmetic very much.
It is the most advanced aircraft carrier in the old Japanese navy.
It was the shortest-lived aircraft carrier in the old Japanese navy.
At the same time, she is the flattest aircraft carrier.
So many first...
Life two, life three, life three things...
Maybe that's why Dafeng likes arithmetic.
One day, she saw such a question:
order
Electrical exploration has found torpedoes from afar, and time is running out.

input
Two non-negative integers separated by spaces in a row are n and p, respectively.

output
One line represents the answer.

sample input
Duplicate sample data
5 97
sample output
11

Tips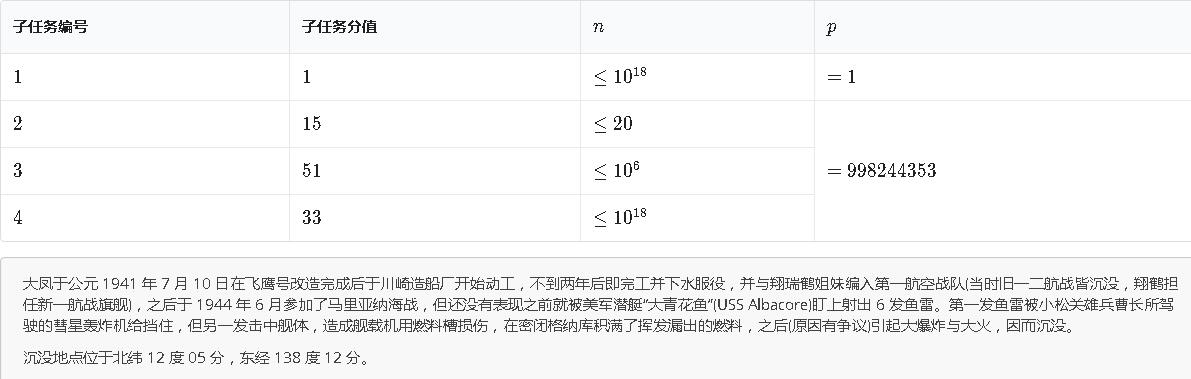

Ideas for solving problems:
By typing the table,

It can be deduced that the value dp[n]dp[n]dp[n] dp[n]dp[n]dp[n] satisfies xn lfloor x ^ n rfloor xn:
dp[n]=f[n]+f[n 2]dp[n]=f[n]+f[n-2]dp[n]=f[n]+f[n 2], that is, dp[n]=f[n] = f[n 1] + 2 f[n 2]dp[n]=f[n-1]+2*f[n-2]dp[n]=f[n] = f[n 1] + 2 f[n-2] dp[n]=f[n] + 2 2
When n n%2==1n:dp[n]dp[n]dp[n]
Otherwise: dp[n]1dp[n]-1dp[n]1
Therefore, dp[n]dp[n]dp[n] DP [n] DP [n] can be quickly calculated by matrix fast power.
∣dp[n]f[n]f[n−1]000000∣\begin{vmatrix} dp[n] & f[n] & f[n-1]\\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{vmatrix}∣∣∣∣∣∣​dp[n]00​f[n]00​f[n−1]00​∣∣∣∣∣∣​ =∣0f[1]f[0]000000∣\begin{vmatrix} 0& f[1] & f[0]\\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{vmatrix}∣∣∣∣∣∣​000​f[1]00​f[0]00​∣∣∣∣∣∣​*∣000111211∣n\begin{vmatrix} 0 & 0 & 0\\ 1 & 1 & 1 \\ 2 & 1 & 1 \end{vmatrix}^n∣∣∣∣∣∣​012​011​011​∣∣∣∣∣∣​n
Therefore, the value of dp[n]dp[n]dp[n] DP [n] can be obtained by matrix fast power, and then discussed according to the parity classification of nnn.
ps: It's necessary to judge the case of nnn 0.
Code:

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <bitset>
#include <set>
#include <utility>
#include <sstream>
#include <iomanip>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define inf 0x3f3f3f3f
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define lep(i,l,r) for(int i=l;i>=r;i--)
#define ms(arr) memset(arr,0,sizeof(arr))
//priority_queue<int,vector<int> ,greater<int> >q;
const int maxn = (int)1e5 + 5;
const ll mod = 1e9+7;
struct node
{
	ll arr[3][3];
	node() {
		ms(arr);
	}
};
ll p;
node mul(node a,node b) {
	node c;
	for(int i=0;i<3;i++) {
		for(int j=0;j<3;j++) {
			for(int k=0;k<3;k++) {
				c.arr[i][j]=(c.arr[i][j]+(a.arr[i][k]*b.arr[k][j])%p)%p;
			}
		}
	}
	return c;
}
ll quickpow(ll n) {
	node a,b;
	a.arr[0][0]=a.arr[0][1]=a.arr[0][2]=a.arr[2][2]=0;
	a.arr[1][0]=a.arr[1][1]=a.arr[1][2]=a.arr[2][1]=1;
	a.arr[2][0]=2;
	b.arr[0][0]=b.arr[0][1]=1;
	b.arr[0][2]=b.arr[1][0]=b.arr[1][1]=b.arr[1][2]=0;
	b.arr[2][0]=b.arr[2][1]=b.arr[2][2]=0;
	while(n) {
		if(n&1) b=mul(b,a);
		a=mul(a,a);
		n>>=1;
	}
	return b.arr[0][0]%p;
}
int main() 
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    #endif
    //freopen("out.txt", "w", stdout);
    //ios::sync_with_stdio(0),cin.tie(0);
    ll n;
    scanf("%lld %lld",&n,&p);
    ll ans=quickpow(n);
    if(n==0) printf("%lld\n",1%p);
    else {
	    if(n%2==1) printf("%lld\n",ans);
	    else {
	    	printf("%lld\n",(ans-1+p)%p);
	    }
	}
    return 0;
}