subject

Given the head node of a linked list, it returns the first node from the linked list into the ring. If the linked list is acyclic, null is returned.

If there is a node in the linked list that can be reached again by continuously tracking the next pointer, there is a ring in the linked list. In order to represent the links in a given linked list, the evaluation system uses the integer pos to represent the position where the tail of the linked list is connected to the linked list (the index starts from 0). If pos is - 1, there is no ring in the linked list. Note: pos is not passed as a parameter, but only to identify the actual situation of the linked list.

Input: head = [3,2,0,-4], pos = 1
 Output: returns the linked list node with index 1
 Explanation: there is a ring in the linked list, and its tail is connected to the second node.

Input: head = [1], pos = -1
 Output: Return null
 Explanation: there are no links in the linked list.

Traversal + hash

The simplest way is to traverse each node and save the node in a dictionary. When traversing the next node, check whether the node pointed to by the next node already exists in the dictionary.

def detectCycle(head: ListNode) -> ListNode:
    hashTable = {}
    while head:
        if head.next in hashTable:
            return head.next
        hashTable[head] = 1
        head = head.next
    return None

Time complexity: O(n)
Space complexity: O(n)

Double pointer

To understand the idea of double pointer, we need to draw a picture and calculate the equivalent relationship of moving distance: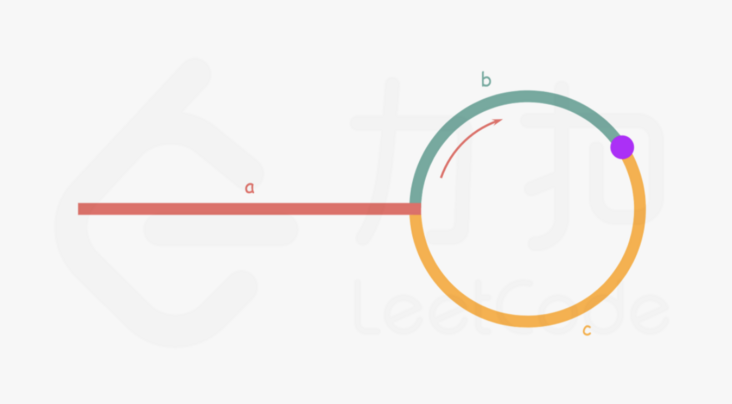

In the chain header node, define two pointers: fast and slow
fast moves 2 nodes at a time and slow moves 1 node at a time

If the linked list has no rings, the fast pointer will first move to null
If the linked list has a ring, fast enters the ring first, slow then enters the ring, and eventually they will meet at a node in the ring

Suppose that the node when fast and slow meet for the first time is as shown in the figure
a represents the number of nodes from the chain header node to the ring entry node
b represents the number of nodes from the entry node of the ring to the node where fast and slow meet for the first time
c represents the number of nodes from the first encounter node to the entry node of the ring

At this time, the number of nodes fast passes through is a+b+n(c+b), and N represents the number of turns fast makes in the ring
The number of nodes passed by slow is a+b
Fast and slow move together, so they move in the same number of steps at any time, but fast moves two nodes at a time. Under the same number of steps, fast should move twice as many nodes as slow
So a+b+n(c+b) = 2(a+b)
Sorting out the equation: a=n(b+c)-b = nb+nc-b = (n-1)b+nc = (n-1)b+(n-1)c+c=(n-1)(b+c)+c
Get a = (n-1)(b+c)+c
That is, the distance from the head node to the ring entry node = the distance from the first encounter node to the ring entry node + (n-1) the length of the ring
If there are two pointers A and b at this time, a moves from the beginning node, b moves from the node where slow and fast meet for the first time, moving one node at a time, and a and b will eventually meet at the ring entry node.
At this time, slow is already in the position of the first encounter node. Therefore, when slow and fast meet for the first time, define a pointer at the head node and move one node with slow at a time. The node they meet is the ring entry node.

def detectCycle(self, head: ListNode) -> ListNode:
    # Exclude empty linked list
    if not head:
        return None
    fast,slow,ptr = head,head,head

    while fast:
        # Exclude the case that the linked list has only one node
        if not fast.next:
            return None
        # Move fast and slow
        slow = slow.next
        fast = fast.next.next
        # When fast and slow meet
        if slow == fast:
            # ptr and slow begin to move until they meet
            while ptr != slow:
                slow = slow.next
                ptr = ptr.next
            # When meeting, return to this node, which is the entry node
            return ptr       
    return None

# Simple and elegant version
def detectCycle(self, head: ListNode) -> ListNode:
    fast, slow = head, head
    while True:
        if not (fast and fast.next): return
        fast, slow = fast.next.next, slow.next
        if fast == slow: break
    fast = head
    while fast != slow:
        fast, slow = fast.next, slow.next
    return fast

Time complexity: O(N), where N is the number of nodes in the linked list. When judging whether the fast and slow pointers meet at first, the distance traveled by the slow pointer will not exceed the total length of the linked list; Then, when looking for the entry point, the distance will not exceed the total length of the linked list. Therefore, the total execution time is O(N)+O(N)=O(N).

Space complexity: O(1). We only use three pointers: slow, fast and PTR.