Catalog

1. Preface

2. Introduction of Stack Content

3. Sequence stack

Chain Stack

V. Summary

1. Preface

This paper mainly introduces the related knowledge of stack and some basic operations of stack. The encapsulated sequential stack and chain stack code are given for direct replication.

2. Introduction of Stack Content

A stack is a linear table that restricts insert or delete operations only at the end of the table. Simply speaking, it can only insert and delete operations at the port at the end of the table, which is simpler than a linear table. Therefore, for a stack, the end of the table is called the top of the stack, the end of the table is called the bottom of the stack, and the stack without elements is called the empty stack.

Assuming a1, a2,..., an elements are stacked in turn, A1 is the bottom element and an is the top element. If insertion and deletion (i.e., in and out) occur at the top of the stack at this time, the first element of the stack is an, so the modification of the stack is based on the principle of LIFO, as shown in the following figure. Therefore, the stack is also known as the linear form of Last In First Out (LIFO).

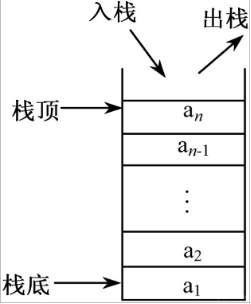
3. Sequence stack

A sequential stack is a stack implemented using a sequential storage structure, and the following code is implemented using a one-dimensional array. Base is the bottom pointer, always pointing to the bottom of the stack, top is the top pointer, always pointing to the top element of the stack, if the stack is empty, top==base. As shown in the following figure

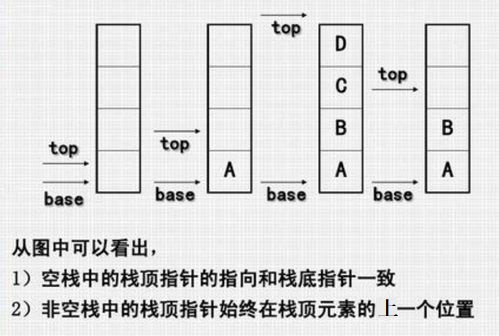
The next step is to give the implementation of the complete code directly, see the code comments for the specific steps.

template<class T>
class SqStack
{
private:
	T *top;		//top of stack
	T *base;	//Bottom stack pointer
	int m_capacity;	//Maximum capacity of stack

public:
	//Constructor, Initialization Stack
	SqStack(int capacity)
	{
		base = new T[capacity];	//Allocate array space in heap area
		top = base;	//top initialization points to base, empty stack
		m_capacity = capacity;
	}
	//Destructor, destroy stack
	~SqStack()
	{
		delete [] base;
	}
	//Judging stack is empty, empty returns true, non-empty returns false
	bool empty()
	{
		if(top == base)
			return true;
		return false;
	}
	//The stacking of a sequential stack
	void push(T e)
	{
		if(top - base == m_capacity)//Full stack
		{
			cout << "SqList::push()The call failed and the stack was full and could not be stacked." << endl;
			exit(-1);
		}
		//Element e is pushed to the top of the stack, the top pointer is added 1
		*top++ = e;	//*top = e; top++;
	}
	//Stack Out of Sequence Table
	void pop(T &e)
	{
		//Determine if stack is empty
		if(empty())
		{
			cout << "SqList::pop()Call failed, empty stack cannot be stacked." << endl;
			exit(-1);
		}
		//The top pointer is subtracted by 1, and the top element is assigned to e
		e = *--top;	//--top; e = *top;
	}
	//Remove top stack element
	T getTop()
	{
		if(empty())
		{
			cout << "SqList::getPop()The call failed because the stack was empty and the top element could not be removed." << endl;
			exit(-1);
		}
		//Returns the value of the top stack element, with the top pointer unchanged
		return *(top - 1);
	}
};

Chain Stack

A chain stack is a stack implemented with a chain storage structure, usually represented by a single-chain table, as illustrated below.

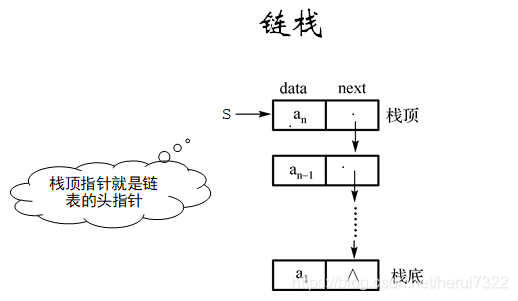
Next, the implementation of the complete code is given, and the steps are described in the code comments.

#pragma once
#include<iostream>
using namespace std;

//Storage structure of chain stack nodes
template<class T>
struct StackNode
{
	T data;//Data Domain
	StackNode *next;//Pointer field
};

//Chain Stack Template Class
template<class T>
class LinkStack
{
private:
	StackNode<T> *s;//top of stack
	
public:
	//Constructor, construct an empty stack
	LinkStack()
	{
		//Stack top pointer empty
		s = NULL;
	}
	//Destructor, destroy chain stack
	~LinkStack()
	{
		
		StackNode<T>* p = NULL;
		while (s)
		{
			p = s;
			s = s->next;
			delete p;
		}
	}
	//Judging stack empty
	bool empty()
	{
		if(s == NULL)
			return true;
		return false;
	}
	//Stacking of Chain Stack
	void push(T e)
	{
		//Create a new node, data field location e
		StackNode<T> *p = new StackNode<T>;
		p->data = e;
		//Insert a new node at the top of the stack
		p->next = s;
		//Reset stack top to p
		s = p;
	}
	//Stack Out of Chain Stack
	void pop(T &e)
	{
		//Determine if stack is empty
		if(empty())
		{
			cout << "LinkStack::pop()The call failed because the chain stack was empty and could not be stacked." << endl;
			system("pause");
			return;
		}
		//The top element of the stack is assigned to e
		e = s->data;
		//Node p temporary storage s
		StackNode<T>* p = s;
		//Update stack top pointer
		s = s->next;
		//Release p
		delete p;
	}
	//Take the top element of the chain stack, return the top element, do not modify the top pointer
	T getTop()
	{
		//Send blank
		if(empty())
		{
			cout << "LinkStack::getTop()The call failed because the stack was empty and the top element could not be removed." << endl;
			system("pause");
			exit(1);
		}
		return s->data;
	}
};

V. Summary

Thank you for your observation. If there are any mistakes or confusing places you can comment on, I will respond to them one by one. Data structure updates will continue.