tips
• avoid falling into the swamp of 'definition' and 'concept', and try to understand it with intuition and natural cognition
• intuitive understanding of algorithm ideas and processes > > details
• it is recommended to use full time to learn and master at one time
I Basic concept of graph (many to many logical structure)
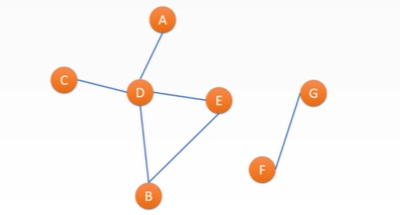
• suppose ABCDEFG is seven telephones, and the connection between them indicates that there is a communication line
• the phone is the vertex of the graph
, the communication line is the side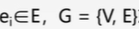
It's a graph.
• as long as there is a line between two phones, you can talk to each other = > undirected graph
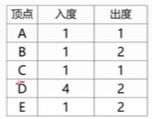
• number of lines (edges) connected by telephone (vertex): degrees
• message cannot be delivered between ABCDE and GF: not connected
• ABCDE and GF are two connected components
• suppose ABCDE is five telephones, the connection between them indicates that there is a communication line, and the number indicates the telephone charge of the line
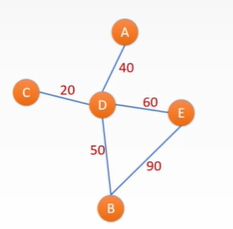
• different telephone charges on different communication lines: weighted diagram
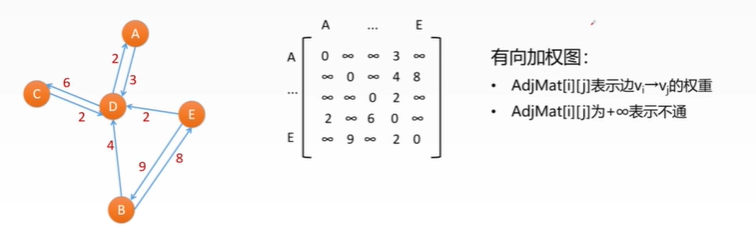
• suppose ABCDE is five cities, and the line with arrow indicates that there are flights operating in this direction
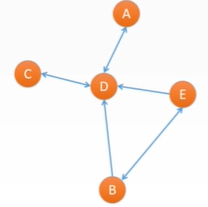
• for example, flight A - > can only support A to D, and the side is one-way = > digraph
• number of flights to a certain place: in degrees
• number of flights departing from a certain place:
• the graph can not only represent geographic data, as long as the data elements meet the many to many relationship:
• can represent the friendship between several students = > undirected graph
• can represent the attention / attention relationship of social media = > directed graph
• it can represent the dependency between multiple tasks with different time consuming = > directed weighted graph
....
*key1: in an undirected graph, the sum of the degrees of all vertices is twice the number of edges
*key2: in a directed graph, the sum of the out degrees of all vertices = = the sum of the in degrees of all vertices
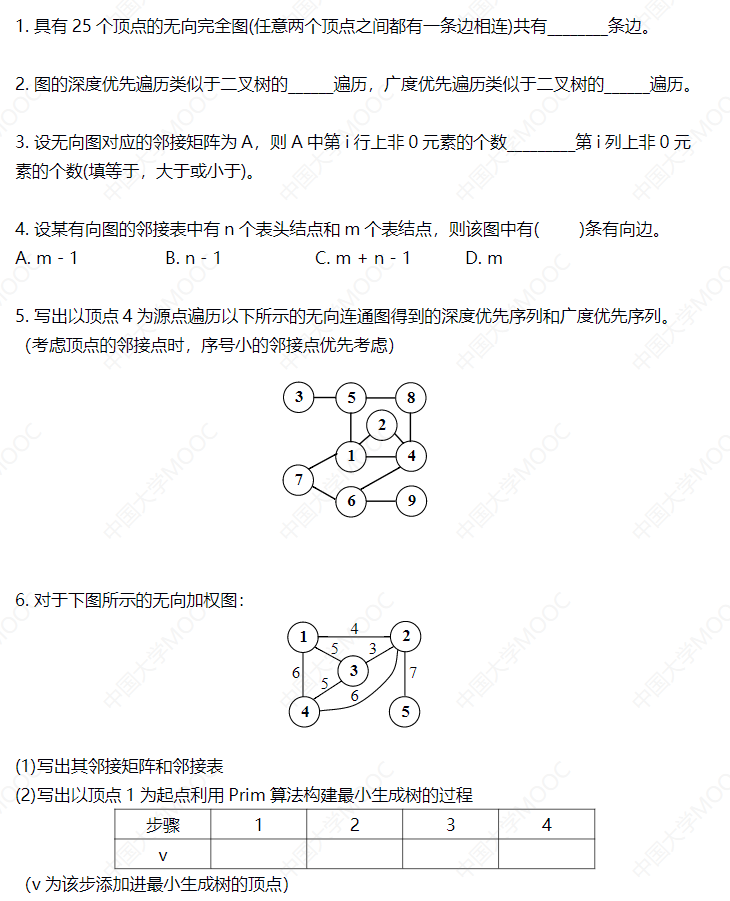
1. In the undirected graph G={V,E}, | V|=n, then the maximum of | E | is? ()
A.n ＾ square of B.n ＾ C.n(n-1) D.n(n-1)/2
analysis:
N nodes, each node has an edge connected with other nodes except itself, and one edge connects two nodes, so the answer is n(n-1)/2
2. Starting from a certain city, you can arrive at all other cities along the expressway with or without transfer, then these cities are (D)
A. Directed B. strongly connected C. weighted D. connected
II Storage structure of graph: adjacency matrix and adjacency table
adjacency matrix
• if | V|=n, the graph can be represented by an n*n square matrix
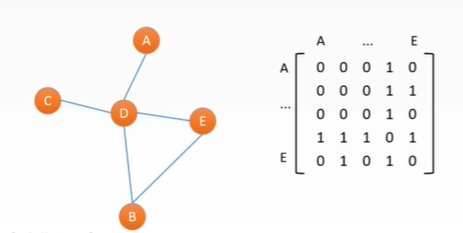
• a two-dimensional array AdjMat[n][n]
• AdjMat[i][j] indicates the adjacency of vi and vj
Undirected graph:
• AdjMat[i][j] is 1, which means there are edges connected, and 0 means there are no edges
• AdjMat is symmetrical
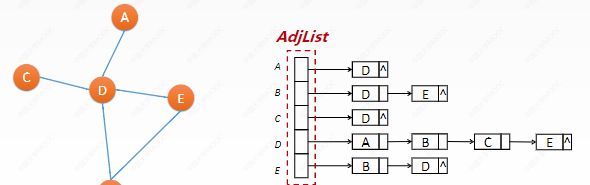
Adjacency table
• each vertex uses a linked list to store its own adjacency
•|V|=n, there are n linked lists, and the graph can be stored in a linked list array AdjList[n]
• AdjList[i] indicates the linked list (header) with vertex vi
• starting from AdjList[i], you can traverse all vi's neighbors
Comparison of adjacency matrix and adjacency table
• let G={V,E},|V|=n
• the adjacency matrix needs a two-dimensional array [n][n] anyway, and the length of each linked list in the adjacency list depends on how many neighbors it has
• adjacency matrix access AdjList[i][j] is O(1), but the adjacency table access specific edge needs to look back along the linked list of the starting point.
• advantages of adjacency table:
• save a lot of space when there are fewer edges = > suitable for sparse graphs
• disadvantages of adjacency table:
• unable to obtain a certain edge information directly, the vi linked list needs to be accessed from scratch, and the worst case is O (n)
III Figure DFS and BFS traversal
Depth First Search
DFS: depth first traversal
• go in when you meet a new neighbor Return until there are no neighbors to enter
• give priority to the neighbors encountered later = > recursion / stack
Breath First Search
BFS: breadth first traversal
• first traverse the neighbors of the current node, and then expand outward layer by layer according to the neighbors who traverse the neighbors first come first.
• priority to enter the neighbor of the first visited neighbor = > queue
• first traverse the neighbors of the current node, and then expand outward layer by layer according to the neighbors who traverse the neighbors first come first.
• priority to enter the neighbor of the first visited neighbor = > queue
*Key1: each step of DFS operation: enter the next unreachable neighbor of the current node, and return if none
*Key2: each step of BFS operation: enter the first node of the current queue and let it out of the queue, and join its unreachable neighbors in the queue
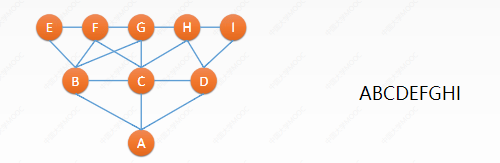
1. Given the following adjacency matrix, write the DFS sequence starting from v0:_________
A.0243156
B.0136542
C.0134256\wa
D.0361542
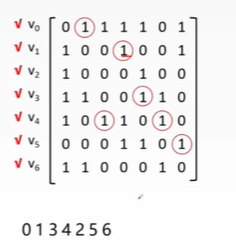
analysis:
1. There is no need to draw the structure diagram
2. Mark the nodes that have been traversed
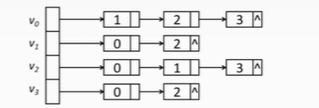
2. Given the following adjacency table, the depth first traversal result from v0 is (D) and the breadth first traversal result is (D).
A.0132
B.0231
C.0321
D.0123
IV Minimum spanning tree (Prim algorithm)
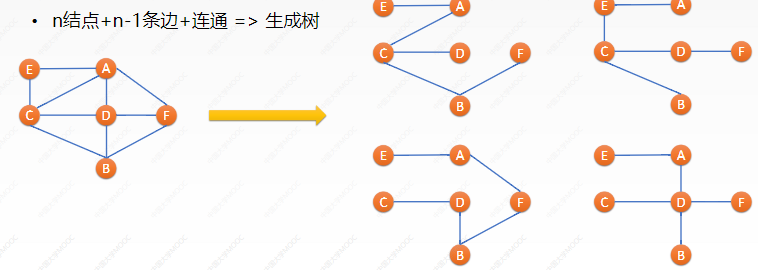
Spanning tree
• for an undirected connected graph with n nodes, the maximum number of edges is n (n-1) / 2 and the minimum is n-1.
• while maintaining connectivity, select n-1 edges and eliminate other edges, and it becomes a tree.
• there are no rings in the spanning tree
Minimum spanning tree MST
• select n-1 edges in the weighted graph to form its spanning tree, and the sum of the weights of these edges is the smallest.
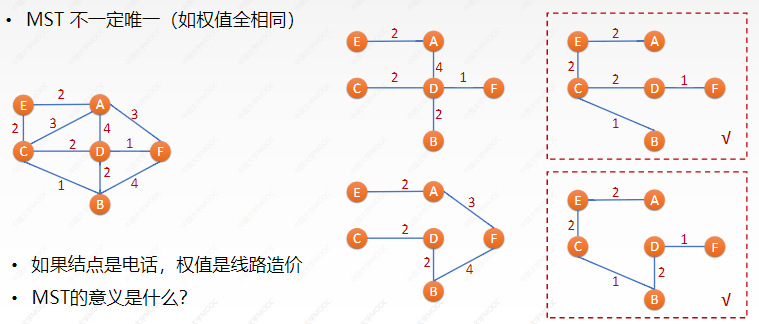Finding the minimum spanning tree: Prim algorithm "point adding method"
• select n-1 edges in the weighted graph to form a spanning tree, and the sum of their weights is the smallest. What strategy is used to select?
• select one of the edges connecting the completed node and the unfinished node with the smallest weight and repeat n-1 times each time
• the algorithm uses the greedy idea: select the local optimum
*key1:Prim algorithm is a point adding method, which gradually adds n-1 points to form MST
*key2:Prim algorithm meets 1 (the minimum weight of the edge to which this point belongs is 2) every time adding points. Adding points will not form a ring
1. Given the structure shown in the figure below, find the minimum spanning tree.
V Dijkstra's algorithm
Single source shortest path: Dijkstra algorithm
• find the shortest distance from a vertex s to other points in the weighted graph
•|V|=n, the algorithm cycles n-1 times, in each cycle:
1. Find the T with the shortest s - > distance among the unfinished nodes and mark t as completed
2. Update the distance of neighbors from s to t with t as the transit
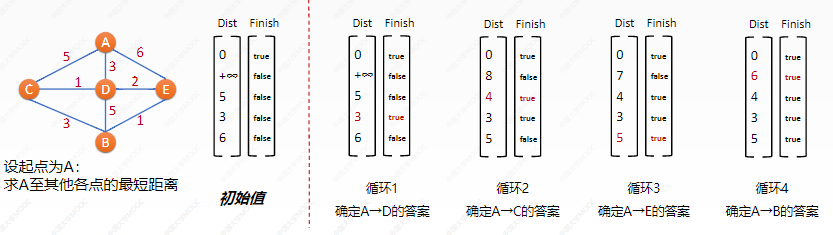
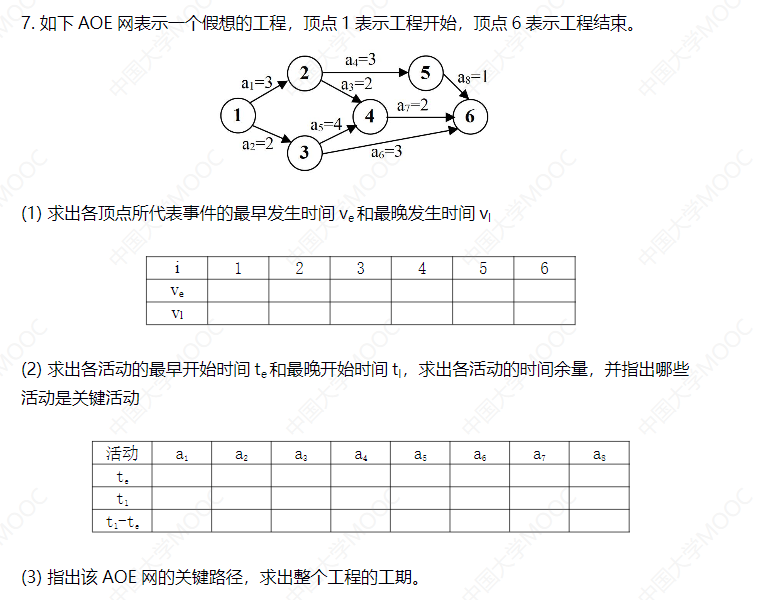
Vi Topological sorting of AOV graph
Topological sorting
• assuming that the vertices in the following directed graph represent different courses and the edges represent the dependencies between courses, can you graduate smoothly?
• yes. Because following the arrow will not produce a ring = > directed acyclic graph (DAG)
• a feasible course selection sequence: 1, 2, 5, 4, 3, 6, 7, 8, 9
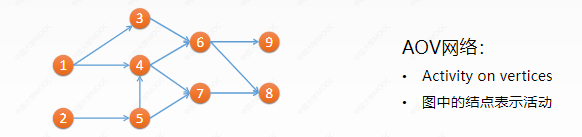
• how to sort topology?
• in short, take the class that can be taken at present (without preamble dependency), and then delete the dependency related to it
• if there are still remaining courses not taken, but there are no courses that can be taken = > topological sorting is not possible = > there are rings in a directed graph
• a feasible course selection sequence: 1, 2, 5, 4, 3, 6, 7, 8, 9
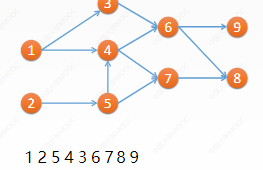
VII AOE network solving critical path
AOE network, critical activities, critical path
• designers, architects, front-end, back-end and testers jointly develop a website:
1. The designer can start work only after designing the front end, the architect can start work only after setting up the back end of the frame, and the front and rear ends can start work only after testing
2. It takes three days for designers, five days for architects, four days for the front end, eight days for the back end and two days for testing
• at least how many days? Who is more critical?
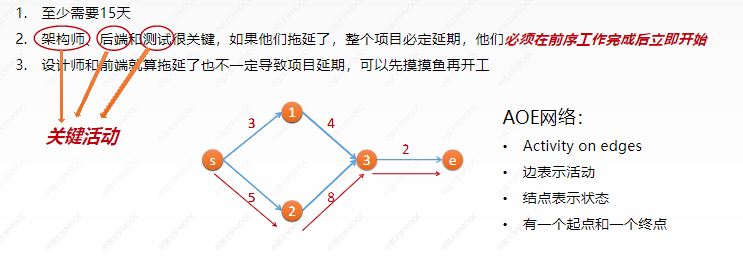
• generally, an AOE network will be given to find key activities and critical paths
• method: calculate the earliest / latest occurrence time VE and VL of each node and the earliest / latest start time eE and eL of each activity
1. According to the topological order, the VE of all nodes is obtained
2. Let the VL of the end point = VE, and calculate the VL of all nodes according to the reverse order of topological sorting
3. The eE of all activities (edges) is equal to the VE of their starting point (an activity can start as soon as the starting point state is reached)
4. The eL of all activities (edges) is equal to the VL wi of their end point (can also be dragged to the last minute)
5. E = el is the key activity, which constitutes the key path
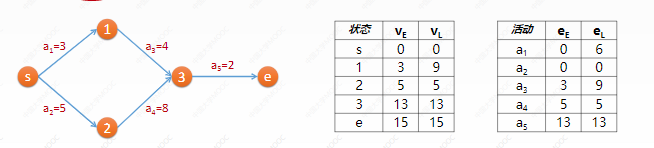
Exercise:
Code:
/*
chart
*/
#include <cstdio>
/* (Undirected graph */
// Adjacency matrix representation
#define N 100
typedef struct GraphAdjMatrix {
int mat[N][N];
} AdjMat;
// Adjacency table representation
typedef struct LinkListNode {
int v;
struct LinkListNode *next;
} ListNode;
typedef struct GraphAdjList {
ListNode *list[N]; // Pointer array, which stores the adjacent header of each node
} AdjList;
// DFS of graph is represented by adjacency matrix
void helper(AdjMat &G, int v, bool *visited) {
// helper is a recursive function that represents the current access node v
printf("%d\n", v);
for (int i = 0; i < N; ++i) {
if (G.mat[v][i] == 1 &&
!visited[i]) { // If v and i are connected and i has not been accessed
helper(G, i, visited); // Access node i
}
}
}
void DFS(AdjMat &G) {
bool visited[N] = {false}; // visited records which nodes have been accessed
for (int i = 0; i < N; ++i) {
if (!visited[i]) { // This loop ensures access to each connected component in G
helper(G, i, visited);
}
}
}
// DFS of graph is represented by adjacency table
void helper(AdjList &G, int v, bool *visited) {
// helper is a recursive function that represents the current access node v
bool visited[N] = {false}; // visited records which nodes have been accessed
printf("%d\n", v);
for (ListNode *p = G.list[v]; p; p = p->next) { // Traverse all neighbors
if (!visited[p->v]) {
helper(G, p->v, visited); // If this neighbor has not been accessed, access it
}
}
}
void DFS(AdjList &G) {
bool visited[N] = {false}; // visited records which nodes have been accessed
for (int i = 0; i < N; ++i) {
if (!visited[i]) { // This loop ensures access to each connected component in G
helper(G, i, visited);
}
}
}
// BFS of graph is represented by adjacency matrix
#include <queue>
void BFS(AdjMat &G) {
bool visited[N] = {false}; // visited records which nodes have been accessed
std::queue<int> q; // Queue memory node number
for (int i = 0; i < N; ++i) { // This loop ensures access to each connected component in G
if (!visited[i]) {
q.push(i); // Start traversing a new connected component
visited[i] = true;
while (!q.empty()) {
int cur = q.front(); // Get the first node number
printf("%d\n", cur); // Visit
q.pop(); // Team first team
for (int i = 0; i < N; ++i) {
int v = G.mat[cur][i];
if (!visited[v]) {
q.push(v); // Traverse all cur neighbors and queue unreachable vertices
visited[v] = true; // Set to accessed to avoid repeated queue entry
}
}
}
}
}
}
// Dijestra algorithm (implementation of adjacency matrix) (only considering that G is a fully connected graph)
void Dijkstra(AdjMat &G, int start) {
int Dist[N]; // Distance array of S - > t
bool finish[N]; // Mark the T of the shortest path of S - > t
// Initialize distance array and completed array
for (int i = 0; i < N; ++i) {
finish[i] = false;
for (int j = 0; j < N; ++j) {
Dist[i] = G.mat[start][i];
}
}
int count = 1; // Record the number of completed nodes. When count == N, the algorithm ends
finish[start] = true;
while (count < N) {
int v = -1, d = INT_MAX;
for (int i = 0; i < N; ++i) {
if (!finish[i] && Dist[i] < d) {
v = i;
d = Dist[i];
}
}
finish[v] =
true; // Find that v is the shortest path in the current unfinished node. This time, determine its answer
count++;
// Then use v transfer to update the shortest distance from the starting point to other nodes
for (int i = 0; i < N; ++i) {
int newDist = d + G.mat[v][i];
Dist[i] = newDist < Dist[i] ? newDist : Dist[i];
}
}
// Show the answer (the following has nothing to do with this algorithm, only for demonstration)
for (int i = 0; i < N; ++i) {
printf("%d -> %d: %d\n", start, i, Dist[i]);
}
}