preface
Heap sort is a sort method with time complexity of O(nlgn). The data structure "heap" is used. This article will answer what is "heap"? How to sort with "heap"?
Binary reactor
First, let's answer what is "heap".
Heap is usually an array object that can be regarded as a complete binary tree. It can be regarded as a structure similar to a binary tree. Except for the bottom layer, other positions are completely filled.
In the heap sorting described in this article, the "binary heap" is used, which is a special heap.
Here is an example:
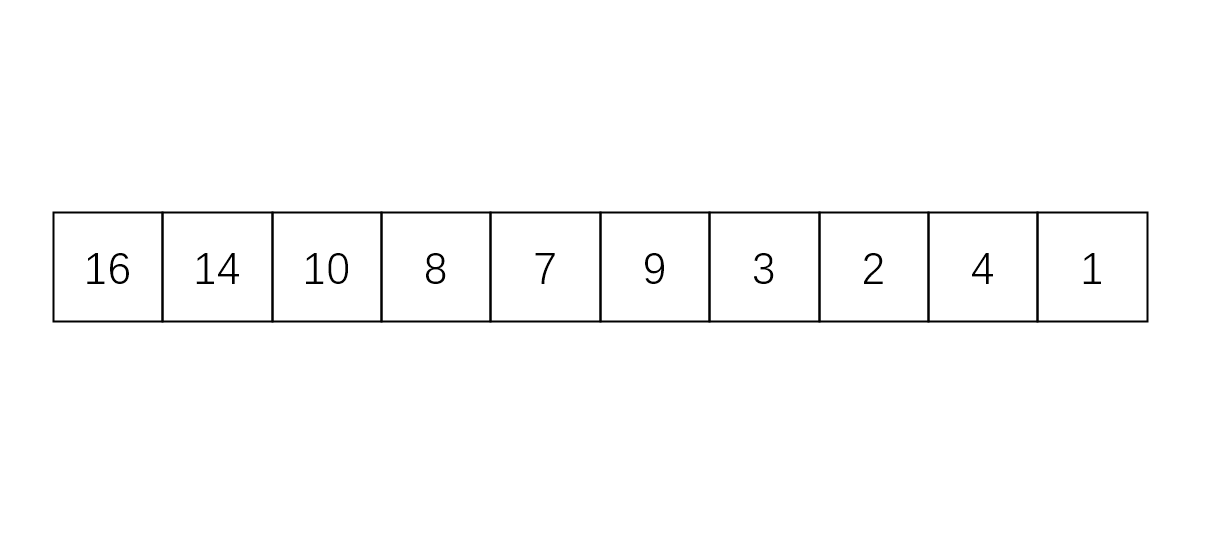
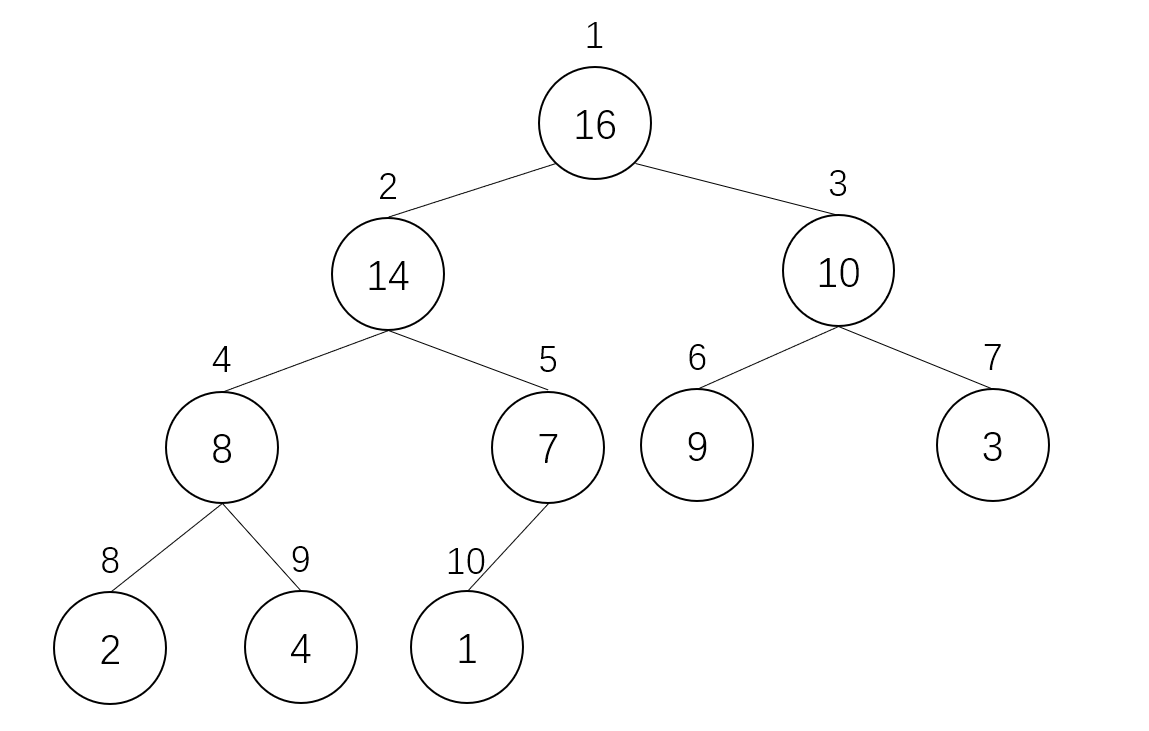
The above figure shows the internal relationship of binary heap in the form of binary tree. The number on each node in the tree represents its position in the array.
Note: in order to correspond the position of the array to the number of nodes in the tree, we mark the beginning and bottom of the array as 1.
As can be seen from the figure, each node also has a left node and a right node, which we call left child and right child. It is not difficult to find that the left child sequence number of a node with sequence number i is 2i and the right child sequence number is 2i+1; The sequence number of the parent node of the left and right children is i/2.
Namely:
//Parent node
int PARENT(int i) {
return i / 2;
}
//Left child
int LEFT(int i) {
return 2 * i;
}
//Right child
int RIGHT(int i) {
return 2 * i + 1;
}A.length and A.heap-size
For an array A, there are two characteristic quantities: the length of the array A.length and the size of the heap A.heap-size. It is worth noting that for array A, to build A heap, you do not need to contain all the elements of A, but the elements in the heap must belong to A. Therefore, there is A.length ≥ A.heap-size. It can be said that given an array A, the A.length has been determined and unchanged, but the A.heap-size also determines how large the heap is formed according to whether the elements at the corresponding position comply with the characteristics of the heap. You will experience the difference between the two when sorting.
Classification of binary reactor
Binary heap can be divided into two forms: maximum heap and minimum heap.
In the maximum heap, the nature of the maximum heap is that all nodes except the root must meet a [parent (I)] ≥ a [i]. That is, the parent node must be greater than or equal to all child nodes.
In the minimum heap, all nodes except the root must meet a [parent (I)] ≤ a [i]. That is, the parent node must be less than or equal to all child nodes.
In the heap sorting in this chapter, we take the maximum heap as an example. The principle of the minimum heap is similar.
Basic operation of binary stack
-
Maintenance heap max-heapify (a, I)
MAX-HEAPIFY is used to maintain the maximum heap nature. Its inputs are array A and subscript i.
When using this operation, there is an important premise: the heap rooted in left (I) and right (I) is the maximum heap. That is, left (I) and right (I) are the maximum of the left subtree and the maximum of the right subtree of I, respectively. The operation of max-heap is to select the largest as the root node in a [i], a [left (I)], a [right (I)], so as to maintain the nature of the largest heap.
For example, we maintain the following heap. Want to maintain the nature of the largest heap at the position a [2] = 4, and its left and right subtrees are the largest heap.
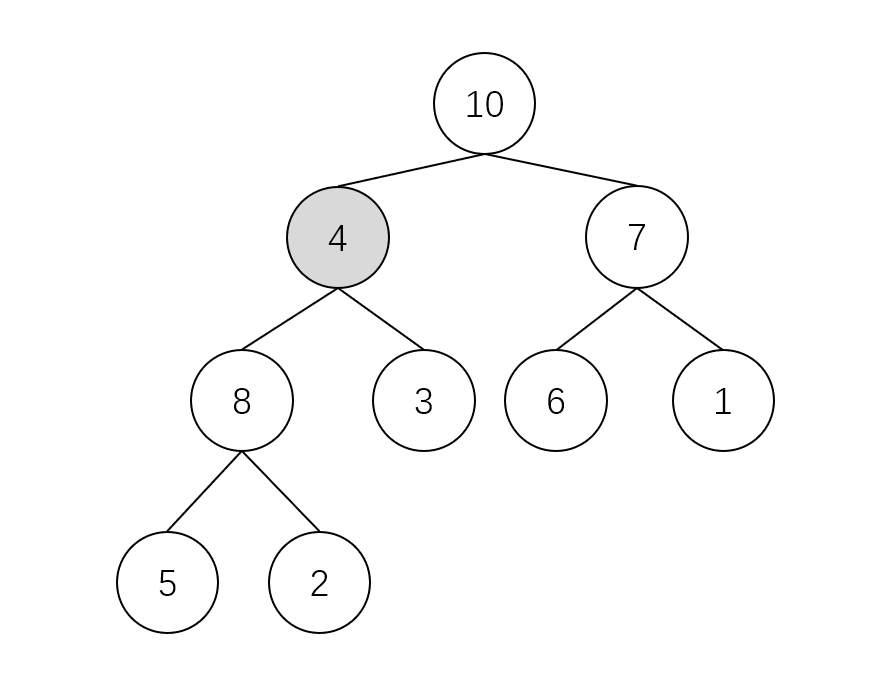
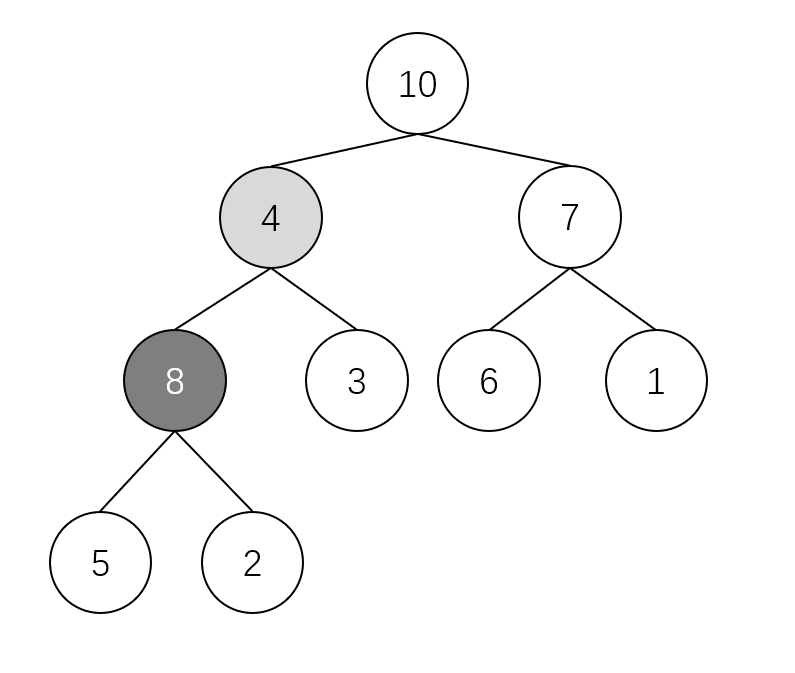
Through the comparison of 4, 8 and 3, it is found that 8 is the largest, so 8 should be the root node, so we naturally exchange 8 and # 4. It becomes the following figure:
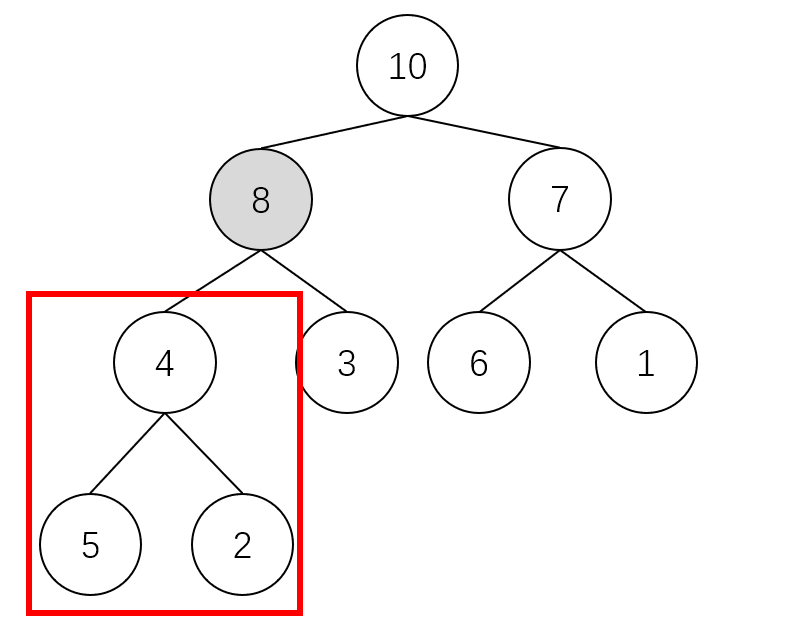
This operation will destroy the maximum heap state of the left subtree, but you only need to re maintain the heap at this position.
Here is the pseudo code for maintaining the heap:
MAX-HEAPIFY( A, i )
1 l = LEFT( i ) r = RIGHT( i )
2 if l ≤ A.heap-size and A[ l ] > A[ i ] largest = l
3 else largest = i
4 if r ≤ A.heap-size and A[ r ] > A[ largest ] largest = r
5 if largest ≠ i
6 swap A[ i ] and A[ largest ]
7 MAX-HEAPIFY( A, largest )
If you can understand the above example, you can understand the code. Lines 1-4 are to find out the root node and the largest items of the left and right children, and then line 5 is to check whether the root node is the largest. If not, it will be exchanged with the largest. Since the exchange will destroy the maximum heap property of the subtree, line 7 is to continue to maintain the maximum heap property of the subtree.
-
Build-max-heap (a)
The purpose of heap building is to convert an array of size A.length into the maximum heap. The maintenance heap operation max-heapify (a, I) is used, but there is a premise for this operation: the left and right subtrees of node i must be the largest heap, which provides a bottom-up design idea for heap building. In other words, the lowest node should be maintained as the largest heap, and then their parent node should be maintained until the root node. This idea is very clear.
Let's look at the pseudo code:
BUILD-MAX-HEAP( A )
1 A.heap-size = A.length
2 for i = ( A.length / 2 ) to 1
3 MAX-HEAPIFY( A, i )
-
Heap sort algorithm HEAPSORT (a)
If you know the nature of the maximum heap, you will know that the root node of the maximum binary heap must be the maximum value of the whole heap element. That is, according to this feature, to sort an array from small to large, you only need to take the largest root node element out of the heap each time and put it at the end of the array, then take the value at the end of the array as the root node, and then maintain the heap again. Just like the following figure:
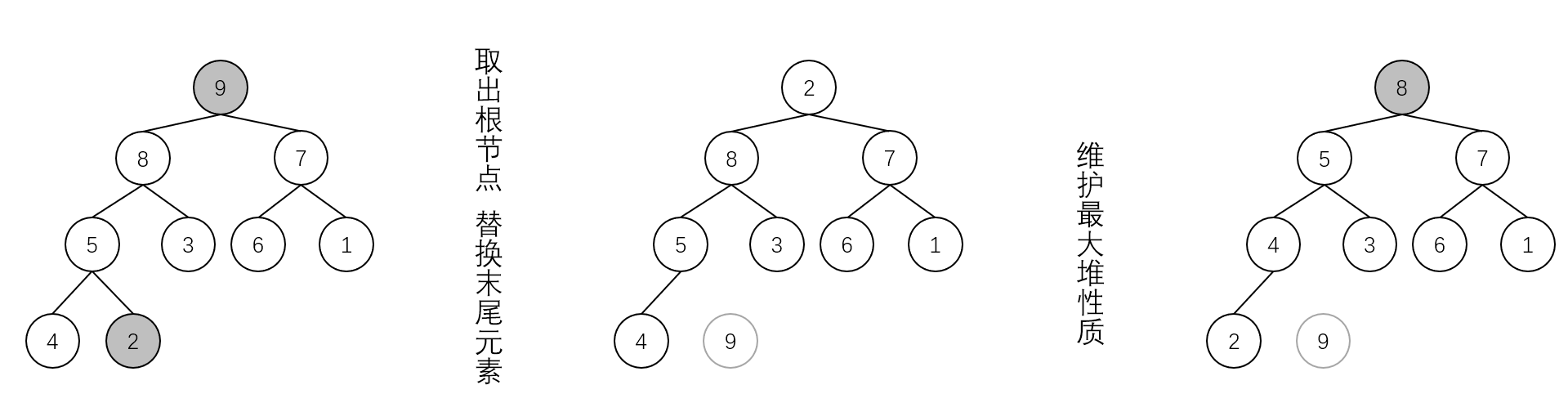
With this A.length-1 operation, we can sort the entire array from small to large.
The pseudo code is as follows:
HEAPSORT( A )
1 BUILD-MAX-HEAP( A )
2 for i = A.length to 2
3 swap A[ 1 ] with A[ i ]
4 A.heap-size - -
5 MAX-HEAPIFY( A, 1 )
The above is the heap sorting algorithm. The specific analysis of time complexity is cumbersome. If you are interested, you might as well deduce it yourself.
Finally, the code of the whole C/C + + implementation is attached:
//Find parent node
int PARENT(int i) {
return i / 2;
}
//Left child
int LEFT(int i) {
return 2 * i;
}
//Right child
int RIGHT(int i) {
return 2 * i + 1;
}
//Maintenance heap (maximum heap)
void Max_Heapify(int* a, const int size, int i) { //Parameters: array, heap size, parent node
int l = LEFT(i); //Get left and right children
int r = RIGHT(i);
int largest; //Create the maximum value, and large is responsible for recording the largest of the three nodes
if (l <= size && a[l] > a[i]) //Compare left child
largest = l;
else
largest = i;
if (r <= size && a[r] > a[largest]) //Compare right child
largest = r;
if (largest != i) { //Parent the largest node
int t = a[i];
a[i] = a[largest];
a[largest] = t;
Max_Heapify(a, size, largest); //Then maintain the position of the replaced number
}
return;
}
//Maintenance heap (minimum heap)
void Min_Heapify(int* a, const int size, int i) { //Parameters: array, heap size, parent node
int l = LEFT(i); //Get left and right children
int r = RIGHT(i);
int smallest; //Create a minimum value, and smallest is responsible for recording the largest of the three nodes
if (l <= size && a[l] < a[i]) //Compare left child
smallest = l;
else
smallest = i;
if (r <= size && a[r] < a[smallest]) //Compare right child
smallest = r;
if (smallest != i) { //Parent the largest node
int t = a[i];
a[i] = a[smallest];
a[smallest] = t;
Min_Heapify(a, size, smallest); //Then maintain the position of the replaced number
}
return;
}
//Build reactor (maximum reactor)
void Build_Max_Heap(int* a, const int length, int size) { //Parameters: array, array length, heap size
size = length;
for (int i = length / 2; i >= 1; i--) {
Max_Heapify(a, size, i);
}
return;
}
//Build reactor (minimum reactor)
void Build_Min_Heap(int* a, const int length, int size) { //Parameters: array, array length, heap size
size = length;
for (int i = length / 2; i >= 1; i--) {
Min_Heapify(a, size, i);
}
return;
}
//Heap sort, from small to large
void Heap_Sort_Up(int* a, int length, int& size) { //Parameters: array, array length, heap size
Build_Max_Heap(a, length, size); //Construct the heap of the array as a whole
for (int i = length; i >= 2; i--) { //From the last item to the second item
int t = a[i]; a[i] = a[1]; a[1] = t; //Take out the root node
size--; //Heap size - 1
Max_Heapify(a, size, 1); //Re maintain the heap
}
return;
}
//Heap sort, from large to small
void Heap_Sort_Down(int* a, int length, int& size) {
Build_Min_Heap(a, length, size); //Construct the heap of the array as a whole
for (int i = length; i >= 2; i--) { //From the last item to the second item
int t = a[i]; a[i] = a[1]; a[1] = t; //Take out the root node
size--; //Heap size - 1
Min_Heapify(a, size, 1); //Re maintain the heap
}
return;
}The summary of this paper is the introduction to personal learning algorithm. If you have any questions, please criticize and correct them in the comment area!