Introduction to data structure
data Structure is computer Storage, organization data The way. A data structure is a structure that has one or more specific relationships with each other data elements A collection of. In general, carefully selected data structures can lead to higher operation or storage efficiency . Data structure is often the same as efficient retrieval algorithm and Indexes Technology related.
Data structure classification
Linear structure:
In short, linear structure is that each node in the table has a linear relationship. If described in the language of data structure, the linear structure should include the following points:
1. Linear structures are nonempty sets.
2. Linear structures have only one start node and one end node
3. All nodes of linear structure have at most one direct forward node and one direct successor node.
Linear table is a typical linear structure, and stack, queue and string all belong to linear structure.
Nonlinear structure
In short, nonlinear structure is that there are multiple corresponding relationships between each node in the table. If described from the language of data structure, the nonlinear structure should include the following points:
1. Nonlinear structures are nonempty sets.
2. A node of a nonlinear structure may have multiple direct forward nodes and multiple direct successor nodes.
In practical application, data structures such as array, generalized table, tree structure and graph structure belong to nonlinear structure.
Arrays and sparse arrays

/**
* Sparse array: sparseArray (Gobang scene)
* Suppose two pieces recorded on a 5 * 10 Gobang board
*/
public class ArrayTest {
@Test
public void commonArray(){
int array [][] = new int[5][10];
array[1][2]=1;
array[2][3]=2;
for (int[] ints : array) {
for (int i : ints) {
System.out.print(i);
}
System.out.println();
}
/*
0000000000
0010000000
0002000000
0000000000
0000000000
*/
}
/**
* Using sparse arrays to simplify,
* sparesArray The first line records the size of the original array and the number of data different from the same data in a large area, and the above array will be simplified to
* 5 10 2
* 1 2 1
* 2 3 2
*/
There are a lot of invalid data in the original array, which occupies a lot of storage space, but there are few really useful data
Compressed storage can save storage space to avoid unnecessary waste of resources. When data is serialized to disk, compressed storage can improve IO efficiency
Convert 2D array to sparse array/**
/** Convert 2D array to sparse array
* @param common
* @return
*/
public int[][] commonToSpares(int[][] common){
//Determine the maximum same value in the two-dimensional array 𞓜 obtain the number different from the maximum same value
//Record the number of occurrences of each number in 0-9 according to the subscript
int nums [] = new int[10];
int rows = 0;
int cols = 0;
for (int[] row : common) {
rows++;
cols=0;
for (int i : row) {
for (int num = 0 ; num < nums.length ; num++) {
if (i==num){
nums[num]++;
break;
}
}
cols++;
}
}
//Gets the number that appears the most, and the number and number of other numbers
int most = 0;
int mostIndex = 0;
int sum = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i]>most){
most = nums[i];
mostIndex=i;
}
sum = sum + nums[i];
}
int otherSum = sum - most;
//After obtaining the number of other elements and the size of the original array, you can create a sparse array
int spares[][] = new int[otherSum+1][3];
//Sets the data for the first row of a sparse array
spares[0][0]=rows;
spares[0][1]=cols;
spares[0][2]=otherSum;
//Set other values for sparse arrays
List<Map<Integer,Integer>> list = new ArrayList<>();
for (int i1 = 0; i1 < rows; i1++) {
for (int i2 = 0; i2 < cols; i2++) {
if (common[i1][i2]!=mostIndex){
Map<Integer,Integer> map = new HashMap<>();
map.put(0,i1);
map.put(1,i2);
map.put(2,common[i1][i2]);
list.add(map);
}
}
}
for (int i = 1; i < spares.length; i++) {
Map<Integer, Integer> integerMap = list.get(i - 1);
spares[i][0]=integerMap.get(0);
spares[i][1]=integerMap.get(1);
spares[i][2]=integerMap.get(2);
}
return spares;
}
Convert sparse array to two-dimensional array
/**
* Convert sparse array to general array
* @return
*/
public int[][] sparesToCommon(int [][] spares){
//1. According to the first row of sparse array, you can create the size of two-dimensional array
int [][] common = new int[spares[0][0]][spares[0][1]];
//2. Determine other values of 2D array
for (int i = 1; i < spares.length; i++) {
common[spares[i][0]][spares[i][1]]=spares[i][2];
}
return common;
}
Persistent sparse array (serialization)
- Prepare classes that can be serialized
/**
* Persistent sparse array
*/
public class SparesArray implements Serializable {
private int[][] sparesArray;
public SparesArray(int[][] sparesArray) {
this.sparesArray = sparesArray;
}
public SparesArray() {
}
public int[][] getSparesArray() {
return sparesArray;
}
public void setSparesArray(int[][] sparesArray) {
this.sparesArray = sparesArray;
}
}
- write in
/**
* Persistent sparse array
* @param sparesArray
* @param file
* @return
*/
public boolean sparesArrayToFiles(SparesArray sparesArray, File file){
boolean flag = false;
try {
ObjectOutputStream obs = new ObjectOutputStream(new FileOutputStream(file));
obs.writeObject(sparesArray);
obs.flush();
flag = true;
obs.close();
} catch (IOException e) {
e.printStackTrace();
}
return flag;
}
- Write
/**
* Convert file to sparse array
* @param file
* @return
*/
public SparesArray fileToSparesArray(File file){
try {
ObjectInputStream ois = new ObjectInputStream(new FileInputStream(file));
return (SparesArray) ois.readObject();
} catch (IOException | ClassNotFoundException e) {
return null;
}
}
queue
- Queue is a special linear table. The special feature is that it only allows deletion at the front of the table and insertion at the back of the table. Like stack, queue is a linear table with restricted operations. The end of insertion is called the end of the queue, and the end of deletion is called the head of the queue.
- It can be understood as first in first out
- Queues can be implemented through arrays and linked lists
Array implementation
package queue;
import java.util.Arrays;
public class ArrayToQueue {
private int maxSize;
private int front;
private int rear;
private Object[] queue;
/**
* Initialize queue: determine the size of the queue according to the size passed by the user
* @param size
*/
public ArrayToQueue(int size) {
maxSize=size;
queue = new Object[size];
front = -1;
rear = -1;
}
/**
* Determine whether the queue is full
*/
public boolean isFull(){
return rear >= maxSize;
}
/**
* Judge whether it is empty
*/
public boolean isEmpty(){
return rear==front;
}
/**
*Add element to queue
* @param o
*/
public void setValue(Object o){
rear++;
if (isFull()){
throw new IndexOutOfBoundsException("Cannot add element because the queue is full");
}else {
queue[rear] = o;
}
}
/**
* Fetch queue element
* @return
*/
public Object getValue(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
front++;
return queue[front];
}
}
/**
* Show all elements of the queue
*/
public void show(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
System.out.println(Arrays.toString(queue));
}
}
/**
* Display header element
*/
public Object getHead(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
return queue[front+1];
}
}
}
Note: in the above code, we cannot realize the reuse of the extracted space, so we need to optimize it.
Optimization: Ring queue is realized by array, which can be realized by taking modulus
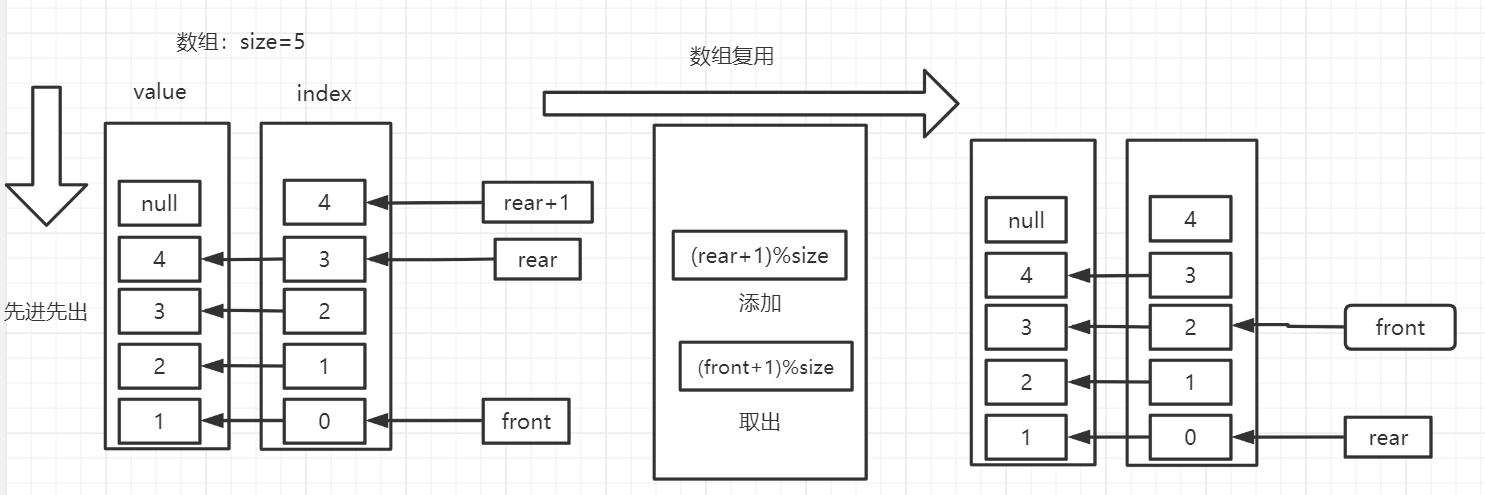
package queue;
import java.util.Arrays;
/**
* Array to implement ring queue
*/
public class RingQueue {
private int maxSize;
private int front;
private int rear;
private Object[] queue;
/**
* Initialize queue: determine the size of the queue according to the size passed by the user
* @param size
*/
public RingQueue(int size) {
maxSize=size;
queue = new Object[size];
front = 0;
rear = 0;
}
/**
* Determine whether the queue is full
*/
public boolean isFull(){
return (rear+1)%maxSize==front;
}
/**
* Judge whether it is empty
*/
public boolean isEmpty(){
return rear==front;
}
/**
*Add element to queue
* @param o
*/
public void setValue(Object o){
if (isFull()){
throw new IndexOutOfBoundsException("Cannot add element because the queue is full");
}else {
queue[rear] = o;
rear = (rear+1)%maxSize;
}
}
/**
* Fetch queue element
* @return
*/
public Object getValue(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
Object a = queue[front];
front = (front+1)%maxSize;
return a;
}
}
/**
* Show all elements of the queue
*/
public void show(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
for (int i = front; i <front+maxSize; i++) {
System.out.println(i%maxSize+"--->"+queue[i%maxSize]);
}
}
}
/**
* Display header element
*/
public Object getHead(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
return queue[front];
}
}
}
Of course, there are many other ways, such as:
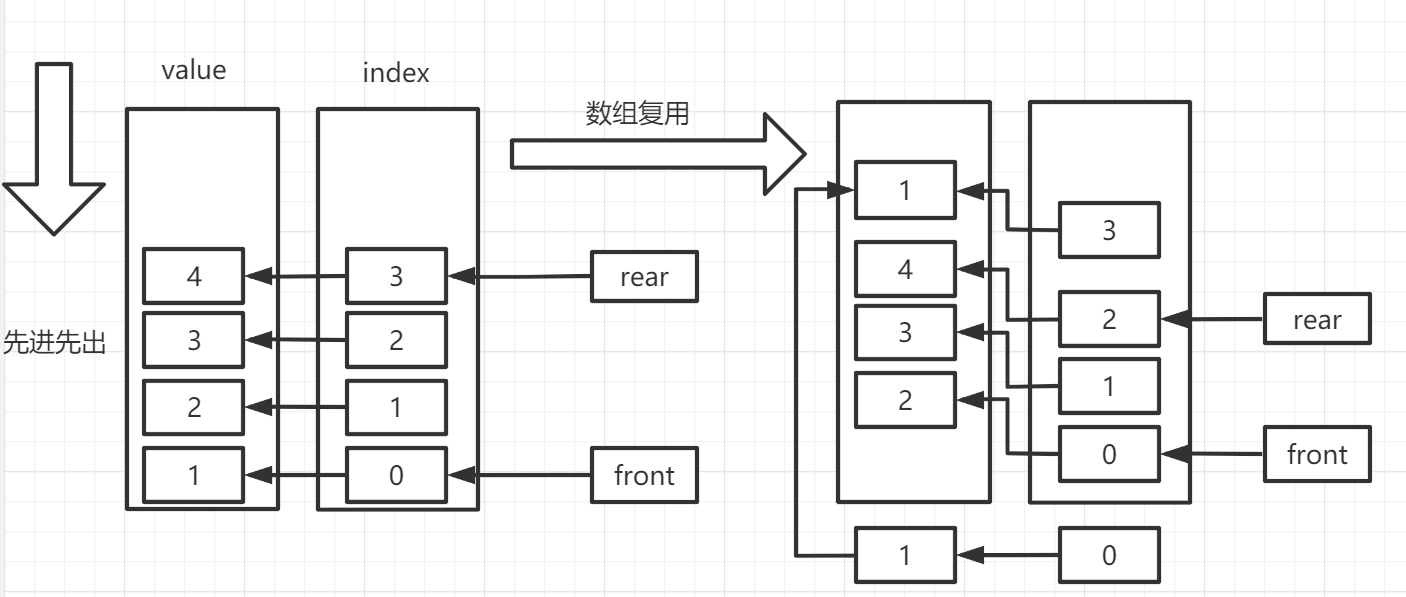
This method is easy to understand, but each pair of column elements will be traversed, and the time complexity will be high. The first implementation scheme is recommended.
package queue;
import java.util.Arrays;
/**
* There are other ways to realize array reuse besides ring queue. There are too many ideas
*/
public class OtherWay {
private int maxSize;
private int front;
private int rear;
private Object[] queue;
/**
* Initialize queue: determine the size of the queue according to the size passed by the user
* @param size
*/
public OtherWay(int size) {
maxSize=size;
queue = new Object[size];
front = 0;
rear = 0;
}
/**
* Determine whether the queue is full
*/
public boolean isFull(){
return rear == maxSize;
}
/**
* Judge whether it is empty
*/
public boolean isEmpty(){
return rear==front;
}
/**
*Add element to queue
* @param o
*/
public void setValue(Object o){
if (isFull()){
throw new IndexOutOfBoundsException("Cannot add element because the queue is full");
}else {
queue[rear] = o;
rear++;
}
}
/**
* Fetch queue element
* @return
*/
public Object getValue(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
Object o = queue[front];
//After taking out the elements, move the array down one bit
for (int i = 0; i < queue.length; i++) {
queue[i]=queue[(i+1)%maxSize];
}
rear--;
return o;
}
}
/**
* Show all elements of the queue
*/
public void show(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
System.out.println(Arrays.toString(queue));
}
}
/**
* Display header element
*/
public Object getHead(){
if (isEmpty()){
throw new NullPointerException("The queue is empty and cannot fetch the element");
}else {
return queue[front];
}
}
}
Linked list
- Linked list is a non continuous and non sequential storage structure on the physical storage unit. The logical order of data elements is realized through the pointer link order in the linked list. A linked list consists of a series of nodes (each element in the linked list is called a node), which can be generated dynamically at runtime. Each node includes two parts: one is the data field for storing the data element, and the other is the pointer field for storing the address of the next node. Compared with the linear list sequential structure, the operation is complex. Because it does not have to be stored in order, the linked list can reach O(1) when inserted The complexity of is much faster than that of another linear table sequential table, but it takes O(n) time to find a node or access a node with a specific number, while the corresponding time complexity of linear table and sequential table are O(logn) and O(1) respectively.
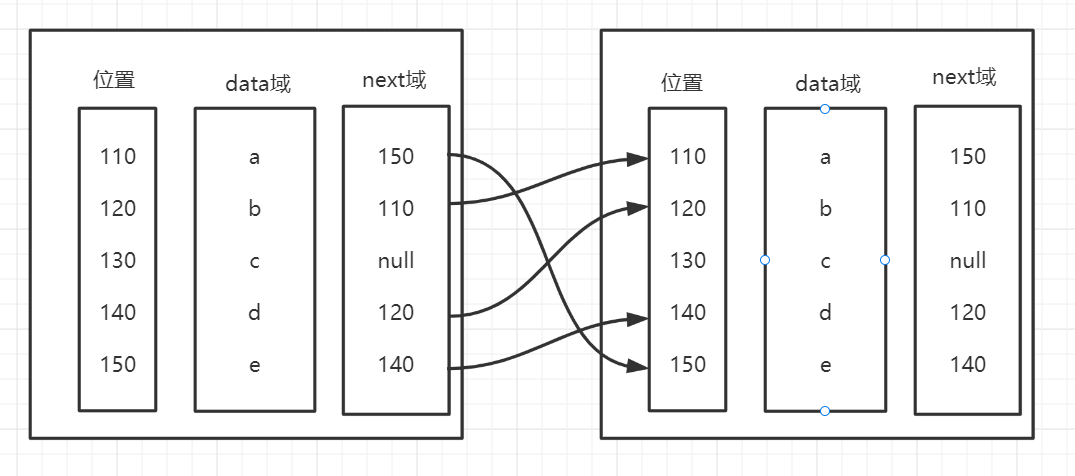
Implement a linked list to complete the simple operation of adding, deleting and modifying the linked list.
package linkedList;
/**
* Simulate a simple linked list. The idea is:
* 1. You can define a header node to specify the starting position of the linked list. The header node does not change. You can define the value field and the next field
* 2. Initialize the header node (the header node should be determined according to the business requirements)
* 3. Add, delete, modify query
*/
public class SimpleLinkedList {
//Initialization of linked list
private Student head = new Student(0,"",0);
//Add linked list node
//Without considering sorting the student id, the newly added linked list is placed directly after the node with next=null
public void addValue(Student newNode){
//Set a variable to dynamically point to each node to facilitate traversal
Student temp = head;
//ergodic
while (true){
if (temp.next==null){
temp.next = newNode;
break;
}
temp = temp.next;
}
}
//Insert in the case of sorting. If the number is the same from low to high, an error will be reported
public void addValueById(Student newNode){
//0 1 5
//The auxiliary variable points to the header node
Student temp = head;
//Loop through the node to find the appropriate insertion position
while (true){
if (temp.next==null){ //Process the first inserted element
temp.next = newNode;
break;
}
if (newNode.id>temp.next.id){ //Get its location and insert
newNode.next=temp.next;
temp.next=newNode;
break;
}
if (newNode.id==temp.id||newNode.id==temp.next.id){ //report errors
System.out.println("The node already exists");
break;
}
temp = temp.next;
}
}
//The linked list is modified according to the id of the object. If the id does not exist, an error is reported
public void updateList(int id ,String name,Double score){
Student temp = head;
while (true){
if (temp.next==null){
System.out.println("The element does not exist in the linked list");
break;
}
if (temp.next.id==id){
temp.next.name=name;
temp.next.score=score;
System.out.println("Successfully modified to:");
System.out.println(temp.next);
break;
}
temp=temp.next;
}
}
//Delete linked list
public void deleteNode(int id){
Student temp = head;
while (true){
if (temp.next==null){
System.out.println("The element does not exist");
break;
}
if (temp.next.id==id){
if (temp.next.next!=null){
temp.next=temp.next.next;
break;
}else {
break;
}
}
temp = temp.next;
}
}
//Inversion of single linked list
public void reversalList(){
//Initialize the linked list and receive the header node
Student temp1 = head.next;
//Customize a new head node, which is realized by the mutual transformation of two linked lists
Student temp2 = new Student(0,"",0);
if (temp1==null){
System.out.println("The linked list is empty");
}else {
while (true){
Student loop = null;
if (temp1==null){
head.next = null;
head.next = temp2.next;
System.out.println("Reverse complete");
break;
}
loop = temp2.next;//null,1,2
temp2.next=temp1;//3 2 1
temp1 = temp1.next;//1-2 2-3 3-null
temp2.next.next=loop;//1-=null,2-1-null
}
}
}
//Print linked list in reverse order
public void printlnList(){
Stack<Student> stack = new Stack<>();
Student temp = head;
if (temp.next==null){
System.out.println("The linked list is empty");
}else {
while (true){
if (temp.next==null){
break;
}
stack.add(temp.next);
temp=temp.next;
}
}
while (stack.size()>0){
System.out.println(stack.pop());
}
}
//View linked list elements
public void showList(){
//Set a variable to dynamically point to each node to facilitate traversal
Student temp = head;
if (temp.next==null){
System.out.println("The linked list is empty");
}
//ergodic
while (true){
if (temp.next==null){
break;
}
System.out.println(temp.next);
temp = temp.next;
}
}
}
class Student{
Integer id;
String name;
double score;
Student next;
public Student(Integer sId, String sName, double sScore) {
this.id = sId;
this.name = sName;
this.score = sScore;
}
@Override
public String toString() {
return id+"---->"+name+"----->"+score;
}
}
Bidirectional linked list
- In the above one-way linked list, when querying, you can always find it in one direction.
- A single linked list cannot be deleted by itself. Each deletion depends on the previous node.
- Bidirectional linked list can be self deleted.
Bidirectional linked list, also known as double linked list, is a kind of linked list. There are two pointers in each data node, pointing to the direct successor and direct precursor respectively. Therefore, starting from any node in the two-way linked list, you can easily access its predecessor node and successor node. Generally, we construct a two-way circular linked list.
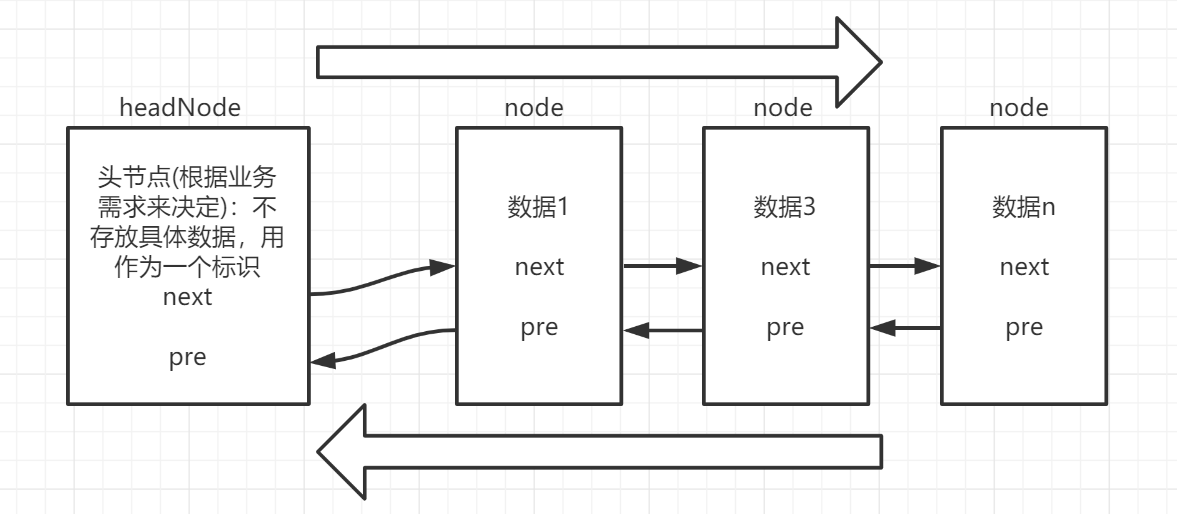
package linkedList;
/**
* Simulate the addition, deletion, modification and query function of two-way linked list
*/
public class BidirectionalLinkedList {
//Initialize a header node
public Person head = new Person(0, "0");
//The default method is to add directly to the back of the linked list
public void addValueByDefaultWey(Person newNode) {
Person temp = head;
while (true) {
if (temp.next == null) {
temp.next = newNode;
newNode.pre = temp;
break;
}
temp = temp.next;
}
}
//Display all nodes in the linked list
public void showNodes() {
Person temp = head;
if (temp.next != null) {
while (true) {
if (temp.next == null) {
break;
}
System.out.println(temp.next);
temp = temp.next;
}
} else {
System.out.println("empty......");
}
}
//Modify the data by id of the linked list
public void updateData(int id, String name) {
Person temp = head;
while (true) {
if (temp.next == null) {
System.out.println("No such element");
break;
}
if (temp.next.id == id) {
temp.next.name = name;
break;
}
temp = temp.next;
}
}
//Delete node (self delete)
public void deleteNode(int id){
Person temp = head;
while (true){
if (temp.next==null){
System.out.println("No such element");
break;
}
if (temp.id==id){
temp.next.pre=temp.pre;
temp.pre.next=temp.next;
break;
}
temp=temp.next;
}
}
}
class Person{
public int id;
public String name;
public Person next;
public Person pre;
public Person(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "Person{" +
"id=" + id +
", name=" + name +
'}';
}
}
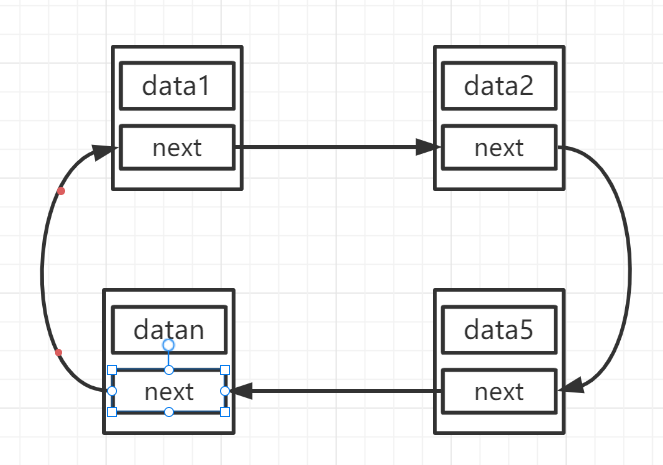
Joseph (ring) problem - one-way linked list to solve
Problem Description: throw a handkerchief: 1-n people form a circle and count off from k. each time they count off 1, when they check in m, that person will be out of the line. After the person listed, one person will count off, and so on. When everyone exits, a number of the queue will be arranged from the beginning to the end.
package linkedList;
import java.util.Scanner;
/**
* Use one-way linked list
* Solve the Joseph problem
*/
public class JosephusProblem {
Children temp = null;
Children head = null;
//Create a new list to accept pop-up elements
Children [] children = null;
int length = 0;
int index = 0;
//Create a ring linked list according to the number of incoming people
public void setList(int num){
//Get the length of the linked list
length = num;
index = num;
for (int i = 0; i < num; i++) {
if (temp==null){
temp = new Children(i);
head = temp;
}else {
temp.next=new Children(i);
temp = temp.next;
}
}
children = new Children[num];
//Let the last element of the linked list point to the first element to form a closed loop
temp.next=head;
for (int i = 0; i < num; i++) {
System.out.println(head);
head = head.next;
}
}
/**
* Determine the elements of the pop-up linked list
* @param id: Represents who to count from
*/
public void getNode(int id){
Children begin = null;
//Find the previous element of the element represented by this id through traversal
if (id<=0){
for (int i = 1; i < length; i++) {
head=head.next;
}
begin=head;
}else {
for (int i = 0; i < length; i++) {
if (head.id==(id-1)){
begin=head;
break;
}
head=head.next;
}
}
System.out.println("The selected element node is:"+begin.next);
Scanner scanner = new Scanner(System.in);
while (true){
if (length==0){
//Indicates that all elements have been ejected
System.out.println("There are no more elements");
break;
}
System.out.println("Please enter the number of times you want to register and pop up the element");
int num = scanner.nextInt()%length;
if (num==0){
num=length;
}
for (int i = 1; i < num; i++) {
begin = begin.next;
}
System.out.println("Out of line:"+begin.next);
children[index-length]=begin.next;
begin.next=begin.next.next;
length--;
}
System.out.println("The order of leaving the queue is");
for (Children child : children) {
System.out.println(child);
}
}
}
class Children{
//Representative number
public int id;
public Children(int id) {
this.id = id;
}
public Children next;
@Override
public String toString() {
return "Children{" +
"id=" + id +
'}';
}
}