3.7 quick sort (quick sort)

Quick sort is an improvement of bubble sort. Its basic idea is to divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so as to turn the whole data into an ordered sequence.
Quick sort and merge sort are similar, except that merge sort is a direct grouping, while quick sort is a required grouping. However, there is no so-called auxiliary array in fast sorting, so it saves some space than merging sorting.

• Requirements:
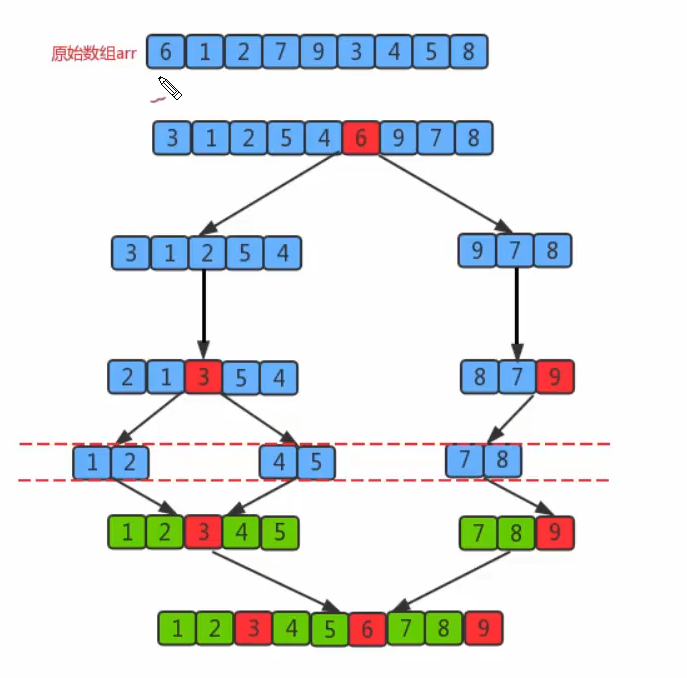
  Before sorting: {6,1,2,7,9,3,4,5,8}
  After sorting: {1,2,3,4,5,6,7,8,9}

• Sorting principle:

1. First, set a boundary value, and divide the array into left and right parts through the boundary value;
2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value;
3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.
4. By repeating the above process, we can see that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed.

• Quicksort API design:
  
• Segmentation principle:

The basic idea of dividing an array into two subarrays:

1. Find a reference value and point to the head and tail of the array with two pointers respectively;
2. First, search for an element smaller than the reference value from the tail to the head, stop the search, and record the position of the pointer;
3. Then, search for an element larger than the reference value from the head to the tail, stop when the search is found, and record the position of the pointer;
4. Exchange the elements of the current left pointer position and the right pointer position;
5. Repeat steps 2 and 3.4 until the value of the left pointer is greater than the value of the right pointer.

• Solve a set of two element problems and matters needing attention

1. Why solve a set of problems with two elements? Because in the actual program operation, we will find that the pointer may search for a group of two elements with left > right. Because when two elements are, the benchmark value is the first element, which is special at this time. We need to write and draw on the draft paper to find some solutions for judging special situations.
2. if right decreases continuously, an if statement must be used to ensure that right cannot be reduced below the initial position of hi.
3. if left continues to increase, an if statement must be used to ensure that left cannot increase to the highest position higher than hi.
4. We must know that no matter what special situation happens, the final lo position and right position will not be wrong!! This is also inevitable. Because our benchmark is on the far left. When right < left, it often comes to the position of the reference value (i.e. special cases).
5. During pointer search, if left > = right is encountered, there is a great chance that it is left > right, so you must break out directly and exchange lo and right! It can complete all handling of special and normal conditions.
6. If you want to include both normal and special situations! Then we need to use the outermost dead cycle. Otherwise, if the loop is dead, it will be over, and there may be fewer cases.

• Quick sort algorithm code

package com.muquanyu.algorithm.sort;

public class Quick {
    /*
    Compare whether element v is less than element w
     */
    private static boolean less(Comparable v,Comparable w){
        return v.compareTo(w) < 0;
    }

    /*
    Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i,int j)
    {
        Comparable temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    /*
    Sort the elements in array a
     */
    public static void sort(Comparable[] a)
    {
        int lo = 0;
        int hi = a.length - 1;
        sort(a,lo,hi);
    }

    /*
    Sort the elements from lo to hi in array a
     */
    private static void sort(Comparable[] a,int lo,int hi)
    {
        //Security verification
        if(lo > hi)
        {
            return;
        }
        //Remember: the index returned by the partition is the boundary value index after grouping
        int partation = partation(a,lo,hi);

        //Order the left subgroup
        sort(a,lo,partation-1);

        //Order the right subgroup
        sort(a,partation+1,hi);


    }

    private static int partation(Comparable[] a,int lo,int hi)
    {
        Comparable key = a[lo];
        //Set two pointers
        int left = lo;
        int right = hi + 1;

        while(true)
        {
            while(less(key,a[--right]))
            {
                if(right == lo)
                {
                    break;
                }
            }
            while(less(a[++left],key))
            {
                if(left == hi)
                {
                    break;
                }
            }
            if(left >= right)
            {
                break;
            }else{
                exch(a,left,right);
            }
        }

        /*while(true)
        {
            while(less(key,a[right]))
            {
                if(right == lo)
                {
                    break;
                }
                right--;
            }
            while(less(a[left],key))
            {
                if(left == hi)
                {
                    break;
                }
                left++;
            }
            if(left >= right)
            {
                break;
            }
            exch(a,left,right);
        }*/
        exch(a,lo,right);
        return right;
    }
}

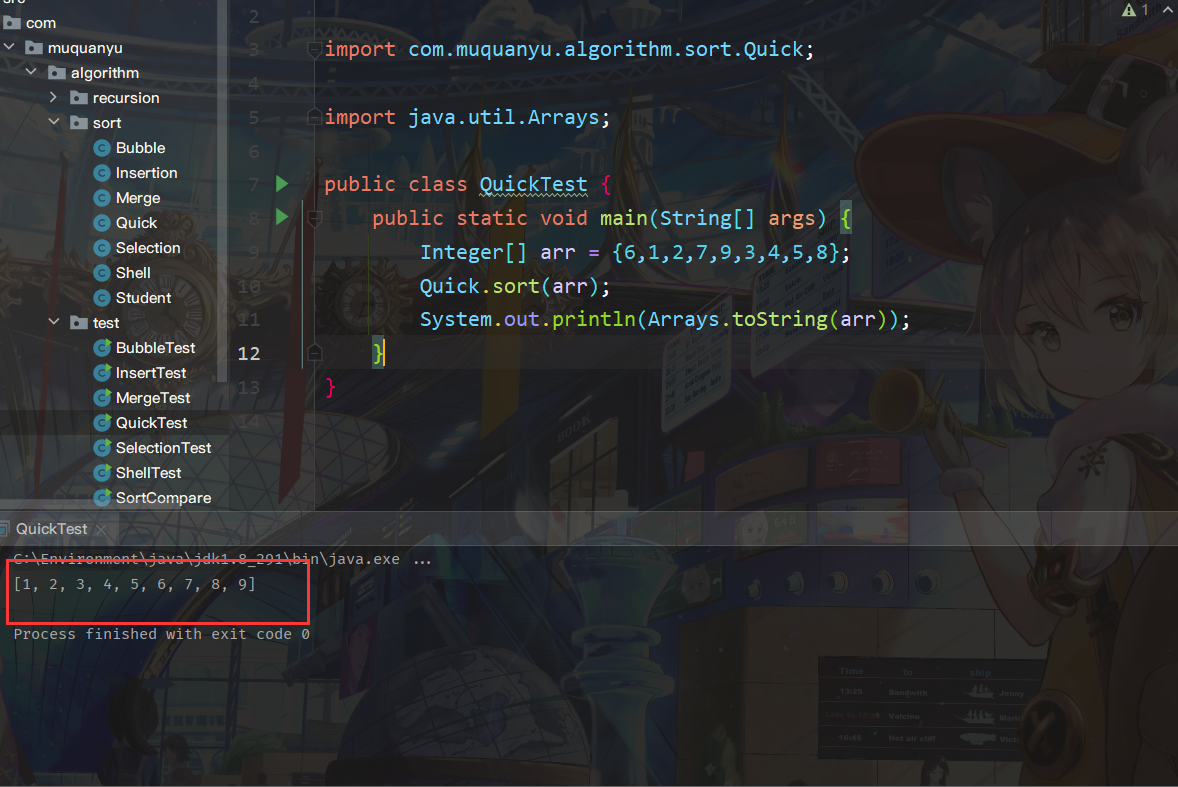
• Quick sort algorithm test

package com.muquanyu.algorithm.test;

import com.muquanyu.algorithm.sort.Quick;

import java.util.Arrays;

public class QuickTest {
    public static void main(String[] args) {
        Integer[] arr = {6,1,2,7,9,3,4,5,8};
        Quick.sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

• Difference between quick sort and merge sort:

Quick sort is another divide and conquer sorting algorithm. It divides an array into two sub arrays and sorts the two parts independently. Quick sort and merge sort are complementary: merge sort divides the array into two sub arrays, sorts them respectively, and merges the ordered sub arrays to sort the whole array. The way of quick sort is that when the two arrays are ordered, the whole array is naturally ordered. In merge sort, an array is equally divided into two parts. The merge call occurs before processing the whole array. In quick sort, the position of the split array depends on the content of the array, and the recursive call occurs after processing the whole array.

• Quick sort time complexity analysis:

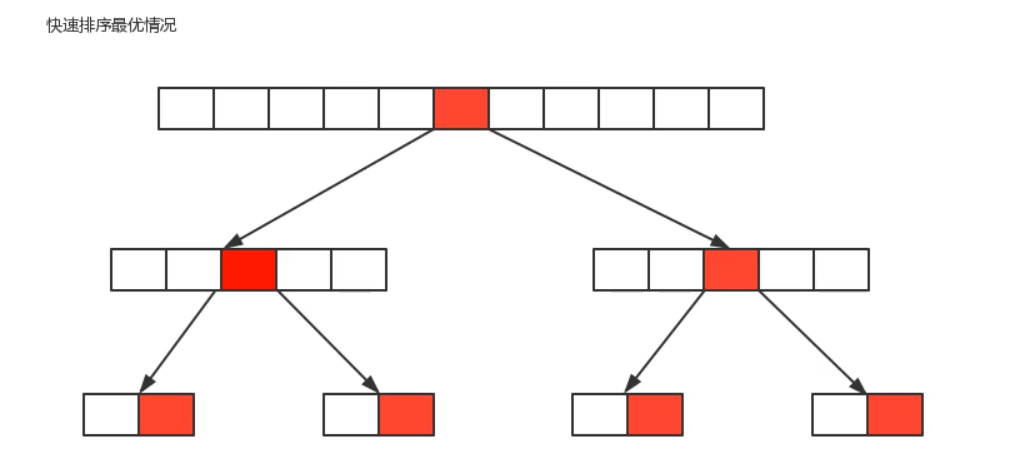
The first segmentation of quick sorting starts from both ends and searches alternately until left and right coincide. Therefore, the time complexity of the first segmentation algorithm is o(n), but the time complexity of the whole quick treatment is related to the number of segmentation.
Optimal situation: the reference number selected for each segmentation just divides the current sequence equally.

Anyway, I'm very slow in measuring fast scheduling. It's not as fast as Hill sorting and merging sorting! I don't know why, the difference is nearly 10 times, and it seems that it is a matter of recursive stack pressing. 10w pieces of reverse order data can't be processed! It directly indicates that the stack overflows.

But officials say the time complexity of fast scheduling is O(n) = n lgn