Data structure and algorithm (C implementation)

Posted by rUmX on Tue, 08 Feb 2022 05:40:00 +0100

Data structure and algorithm (C/C + + implementation)

Chapter 1 C + + review

1.1 C + + preliminary

1. C + + namespace

For example, Xiao Li and Xiao Han both participated in the development of a file management system. They both defined a global variable fp to indicate the previously opened files. When compiling their code together, it is obvious that the compiler will prompt fp for Redefinition errors.

In order to solve the naming conflict in cooperative development, C + + introduces the concept of Namespace. Take the following example:

namespace Li{  //Xiao Li's variable definition
    FILE fp = NULL;
}
namespace Han{  //Xiao Han's variable definition
    FILE fp = NULL
}

Xiao Li and Xiao Han have customized the namespace with their last name. At this time, there will be no problem if they put their fp variables together for compilation.

Namespaces are sometimes called namespaces, namespaces. Namespace is a keyword in C + +. It is used to define a namespace. The syntax format is:

namespace name{
    //variables, functions, classes
}

Name is the name of the namespace, which can contain variables, functions, classes, typedef s, #define, etc., and is finally surrounded by {}.

When using variables and functions, indicate their namespace. Take the fp variable above as an example, you can use it as follows:

Li :: fp = fopen("one.txt", "r");  //Use the variable fp defined by Xiao Li
Han :: fp = fopen("two.txt", "rb+");  //Use the variable fp defined by small Han

:: is a new symbol called domain resolution operator, which is used in C + + to indicate the namespace to be used.

In addition to directly using the domain resolution operator, you can also use the using declaration, for example:

using Li :: fp;
fp = fopen("one.txt", "r");  //Use the variable fp defined by Xiao Li
Han :: fp = fopen("two.txt", "rb+");  //Use the variable fp defined by small Han

Li::fp is declared at the beginning of the code with using, which means that if fp with unspecified namespace appears in the program after ` ` using declaration, Li::fp will be used; However, if you want to use fp defined by Han::fp ', you still need Han::fp'.

The using declaration can be used not only for a variable in the namespace, but also for declaring the entire namespace, for example:

using namespace Li;
fp = fopen("one.txt", "r");  //Use the variable fp defined by Xiao Li
Han :: fp = fopen("two.txt", "rb+");  //Use the variable fp defined by small Han

If other variables are defined in the namespace Li, it also has the effect of fp variables. After the using declaration, if there is a naming conflict caused by a variable that does not specify a namespace, the variable in the namespace Li is adopted by default.

Not only variables can be declared or defined inside the namespace, but also other names that can be declared or defined outside the namespace. For example, classes, functions, typedef s, #define, etc. can appear in the namespace.

2. C + + standard library and std namespace

In order to avoid duplicate header file names, the new C + + library has also adjusted the naming of header files and removed the suffix h. So iostream.com in old c + + H becomes iostream, fsstream H becomes fstream. The same method is used for the header file of the original C language, but a c letter must be added before each name, so stdio H becomes cstdio, stdlib H becomes cstdlib

It can be found that for those without h header file, all symbols are located in namespace std, and namespace std needs to be declared when using; For tape The header file of h does not use any namespace, and all symbols are in the global scope. This is also stipulated in the C + + standard

In C language, we usually use scanf and printf to input and output data. In C + + language, we can still use this set of input and output libraries of C language, but C + + has added a new set of input and output libraries that are easier to use.

The input and output in C + + can be regarded as a series of data streams. The input can be regarded as inputting a series of data streams in the program from the file or keyboard, while the output can be regarded as outputting a series of data streams from the program to the display screen or file. When writing C + + programs, if you need to use input and output, you need to include the header file iostream, which contains the objects used for input and output. For example, the common cin represents standard input, cout represents standard output, and cerr ` represents standard error. Iostream is the abbreviation of Input Output Stream, which means "Input Output Stream". Cout and cin are built-in objects of C + +, not keywords.

3. new and delete operators

In C language, malloc() function is used to dynamically allocate memory and free() function is used to free memory. As follows:

int *p = (int*) malloc( sizeof(int) * 10 );  //Allocate 10 memory spaces of type int
free(p);  //Free memory

In C + +, these two functions can still be used, but C + + adds two new keywords: new and delete: new is used to dynamically allocate memory and delete is used to free memory.

int *p = new int;  //Allocate 1 memory space of type int
delete p;  //Free memory
//The new operator infers the size of the required space based on the following data types.

//If you want to allocate a continuous set of data, you can use new []:
int *p = new int[10];  //Allocate 10 memory spaces of type int
delete[] p;

The memory allocated with new [] needs to be released with delete [] and they correspond to each other one by one.

Like malloc (), new allocates memory in the heap and must be released manually. Otherwise, it can only be recycled by the operating system after the program runs. In order to avoid memory leakage, new and delete, new [] and delete [] operators should usually appear in pairs and should not be mixed with malloc() and free() in C language.

4. Inline inline function

The execution process of a C/C + + program can be regarded as the mutual call process between multiple functions. They form a simple or complex call chain. The starting point of this chain is main(), and the end point is also main(). When main() calls all the functions, it will return a value (for example, return 0;) To end your life and end the whole program.

Function calls have time and space overhead. Before a program executes a function, it needs to do some preparatory work. It needs to push the arguments, local variables, return addresses and several registers into the stack, and then it can execute the code in the function body; After the code in the function body is executed, the site must be cleaned up and the data previously pushed into the stack must be out of the stack before the code after the function call position can be executed.

If there are many function body codes and a long execution time is required, the time occupied by the function call mechanism can be ignored; If the function has only one or two statements, most of the time will be spent on the function call mechanism, which can not be ignored.

In order to eliminate the time and space cost of function call, C + + provides a method to improve efficiency, that is, replace the function call with the function body during compilation, which is similar to the macro expansion in C language. This kind of function directly embedded in the function body at the function call is called ` ` Inline Function ', also known as embedded function or built-in function.

Note that adding the inline keyword at the function definition is not wrong, but it is invalid. The compiler will ignore the inline keyword at the function declaration.

The disadvantage of using inline functions is also very obvious. There will be multiple copies of the same function in the compiled program. If the function body declared as inline functions is very large, the volume of the compiled program will also become large. Therefore, it is emphasized again that generally only those short and frequently called functions are declared as inline functions.

1.2 C + + function improvement

1. Function parameters

1. Value transfer parameter

int abc(int a ,int b,int)
{
	return a+b+c;	
}

a. B and C are formal parameters, and each formal parameter is plastic; You can make z=abc(2,x,y) call the summation function. Then 2, X and Y correspond to the arguments of a, B and C respectively. Formal parameters a, B and C are actually value passing parameters. At runtime, the actual parameters are copied to the formal parameters before the execution of functions a, B and C. The copy procedure consists of a copy constructor of parameter type

2. Default parameters

In C + +, the formal parameters in the formal parameter list of a function can have default values

Syntax: return value type function name (parameter A = default value 1, parameter B = default value 2)

int add(int a, int b = 10, int c = 20)
{
    return a + b + c;
}
//If a location has a default parameter, it must have a default value from this location
//Only one declaration and implementation can have default parameters

/*Error example
int add(int a, int b = 10, int c)
{
    return a + b + c;
}
*/

2. Function overloading

**Function: * * same function name to improve reusability

Conditions satisfied by function overload:

Under the same scope
Same function name
The type, number or order of function parameters are different

int add(int a, int b)
{
    return a + b;
}
int add(int a, int b, int c)
{
    return a + b + c;
}
double add(double a, double b, double c)
{
    return a + b + c;
}

int main()
{
    int m, n;
    cout << " 1 : " << add(1, 2) << endl;
    cout << " 2 : " << add(1, 2, 3) << endl;
    cout << " 3 : " << add(1.1, 2.2, 3.3) << endl;
    system("pause");
    return 0;
}

Precautions for function overloading:

Reference as a condition for function overloading
Function overload encountered default parameter

Note: compiler ambiguity

3. Template function

Suppose we want to write another function to evaluate the same expression, but this time a, b and c are float types, and the result is also float types. The specific code is given in program 1-2. The only difference lies in the types of formal parameters and function return values.

float abc(float a, float b, float c)
{
    return a+b+c;
}

Instead of writing a new version of the corresponding function for each possible parameter type, it is better to write a general code. Its parameter type is a variable, and its value is determined by the compiler. This generic code uses template statements.

template <class T>
T abc(T a, T b, T c)
{
    return a+b+c;
}

From this general-purpose code, the compiler can replace T with int or float. In fact, by replacing T with double or long, the compiler can also construct double and long versions of function abc. If abc function is written as a template function, we don't need to know the type of formal parameter.

1.3 C + + classes and objects

The three characteristics of C + + object-oriented: encapsulation, inheritance and polymorphism. Everything in C + + task is an object, and the object has its properties and behavior.

Each object class can create one or more object types; The process of creating objects is also called class instantiation. Each object is a concrete instance of the class and has member variables and member functions of the class.

Some tutorials refer to the member variable of a class as the Property of the class, and the member Function of a class as the Method of the class. In object-oriented programming languages, functions are often called methods.

class Student
{
public:
    //Property
    string name;
    int old;
    float score;
	//Method
    void StudentInformation()
    {
        cout << "the old of " << name << "is " << old << ","
             << "and his(her) score is " << score << endl;
    }
};

1. Meaning of encapsulation

Three kinds of access rights:

public permission: members can be accessed inside the class and outside the class

protected: members can access inside the class, but not outside the class. Subclasses can access the parent class

private permission: members can access inside the class, but not outside the class. Subclasses cannot access the parent class

class Person
{
public:
    string m_name;
protected:
    int m_car;
private:
    int m_card_ID;
public:
    void func()
    {
        m_name = "zwy";
        m_car = 123;
        m_card_ID = 123456;
    }
};

Set member properties to private

1. You can control the read and write properties yourself

2. For write, data validity can be detected

2. Object initialization and cleanup

1. Constructors and destructors

Constructor syntax: class name () {}

The constructor does not return a value and does not write void
The function name is the same as the class name
Constructors can also have parameters, so overloading can also occur
When the program calls the object, it automatically calls the construct without manual call, and it will only be called once

Destructor syntax: ~ class name () {}

The destructor does not return a value and does not write void
The function name is the same as the class name, and the symbol is added before the name~
Destructors cannot have parameters, so overloading cannot occur
The program automatically calls the destructor when the object is destroyed without manual call, and it will only be called once

class Person
{
public:
    Person()
    {
        cout << "1" << endl;
    }

    ~Person()
    {
         cout << "2" << endl;
    }
};

2. Classification of constructors

Classified by parameters: nonparametric construction (default construction) and parametric construction

Classification by type: copy construction and normal construction (default construction)

//Parametric structure  
Person(int a)
{
    cout << "1" << endl;
}
//copy construction 
Person(const Person &p)
{
    //Copy all the attributes of the incoming class to this one
}

3. Function template

Another programming idea of C + + is called generic programming. The main technology used is template
C + + provides two template mechanisms: function template and class template

Function template syntax:

//definition
template<typename T>
void func(T &a,T &b)
{
    
}
//use
func<datatype>(a,b) ;

Explanation:

Template -- Declaration template

typename -- indicates that it is followed by a data type, which can be replaced by class

T -- General data type, with replaceable name, usually capital letters

Function template function: establish - a general function whose function return value type and formal parameter type can be represented by - Virtual types without specific formulation.

Limitation of function template: suppose there is a class - human, which has two attributes - name and age. Can you directly judge whether it is the same person through the function template?

class Person{
public:
  string _name;
  int _age;
  Person(string name, int age) : _name(name), _age(age){};
  ~Person(){};
};

The following is an example of an error:

/*
template <typename T>
bool func(T &a, T &b)
{
    if (a == b)
        return true;
    else
        return false;
}
void test_1()
{
    Person P1("Tom", 10);
    Person P2("Tom", 10);
    bool re = func(P1, P2);
}*/

resolvent:

template <typename T>
bool func(T &a, T &b)
{
    if (a == b)
        return true;
    else
        return false;
}
template <>
bool func(Person &a, Person &b)
{
    if (a._age == b._age && a._name == b._name)
        return true;
    else
        return false;
}
void test_2()
{
    Person P1("Tom", 10);
    Person P2("Tom", 10);
    bool re = func<Person>(P1, P2);
    cout << re << endl;
}

4. Class template

Class template syntax:

template <class nameType, class ageType = int>
class Person
{
public:
  nameType _name;
  ageType _age;
  Person(nameType name, ageType age) : _name(name), _age(age){};
  ~Person(){};
};

Explanation:

Template -- Declaration template

typename -- indicates that it is followed by a data type, which can be replaced by class

T -- General data type, with replaceable name, usually capital letters

Chapter 2 program performance analysis

2.1 space complexity

1. Composition of spatial complexity
The space required by the program is mainly composed of the following parts:
(1) Instruction space: instruction space refers to the storage space required by the compiled program instructions.

The amount of instruction space depends on the following factors:
● a compiler that converts programs into machine code.
● compiler options at compile time.
● target computer.

(2) Data space: data space refers to the storage space required for all constant and variable values. It consists of two parts:

● storage space required for constants and simple variables.
● space required by dynamic objects such as dynamic arrays and dynamic class instances.

type	Space size	Range
bool	1	{true,flase}
char	1	{-128,127}
unsigned char	1	{0,255}
short	2	{-32768,32767}
unsigned short	2	{0,65535}
long	4	{-231,-231-1}
unsigned long	4	{0,232-1}
int	4	{-231,-231-1}
unsigned int	4	{0,232-1}
float	4	± 3.4E ± 38 (7 bits)
double	8	± 1.7E ± 308 (15 bits)
long double	10	± 1.2E ± 4392 (19 bits)

(3) environment stack space: the environment stack is used to store the number of pauses and the information required by the method when it resumes operation. For example, if the function foo calls the lie number goo, we should at least save the instruction address that the function foo continues to execute at the end of the function goo.

● return address.
● values of all local variables and formal parameters of the function being called (only for recursive functions).

2.2 time complexity

2.3 operation count

2.4 steps

Chapter 3 linear table - array description

3.1 data structure of linear table

Linear list is also called ordered list. Every instance of it is an ordered set of elements. The form of each instance is (e0,e1,e2,e3... en), where n is a finite natural number, ei is the element of the linear table, i is the index of the element ei, and N is the length or size of the linear table. Elements can be regarded as atoms, and their own structure is independent of the structure of the linear table. When n=0, the linear table is empty; When n > 0, e0 is the 0th or first element of the linear table, and en-1 is the last element of the linear table. It can be considered that e0 precedes e1, e1 precedes e2 and so on. In addition to this sequential relationship, the linear table has no other relationship.

Operation on linear table:

Create linear table

ChaLenArray *Init_Array() //Initialize a dynamic array
{
    ChaLenArray *NewArray = (ChaLenArray *)malloc(sizeof(ChaLenArray));
    NewArray->size = 0;
    NewArray->cap = 20;
    NewArray->pAddr = (int *)malloc(sizeof(int) * NewArray->cap);
    return NewArray;
}

Undo a linear table.

void FreeSpace_Array(ChaLenArray *arr) //Free up memory space of a dynamic array
{
    if (arr == NULL)
        return;
    if (arr->pAddr != NULL)
    {
        /* code */
        free(arr->pAddr);
    }
    free(arr);
}

Determine the length of the linear table.

int Size_Array(ChaLenArray *arr)
{
if (arr == NULL)
return -1;
return arr->size;
}

Finds an element by a given index.

int At_Array(ChaLenArray *arr, int pos)
{
    if (arr == NULL)
        return -1;
    return arr->pAddr[pos];
}

Finds the index of a given element by its index.

int Find_Array(ChaLenArray *arr, int value) //Found an element
{
    if (arr == NULL)
        return -1;
    int pos = -1;
    for (int i = 0; i < arr->size; i++)
    {
        if (arr->pAddr[i] == value)
        {
            pos = i;
            break;
        }
    }
    return pos;
}

Deletes -- elements by a given index.

void RemoveByPos_Array(ChaLenArray *arr, int pos) //Delete an element by position
{
    if (arr == NULL)
        return;
    if (pos < 0 || pos >= arr->size)
        return;
    for (int i = pos; i < arr->size - 1; i++)
    {
        arr->pAddr[i] = arr->pAddr[i + 1];
    }
    arr->size--;
}

Inserts - an element at a given index.

void Push_Back_Array(ChaLenArray *arr, int value) //Insert a data in the tail
{
    if (arr == NULL)
        return;
    if (arr->size >= arr->cap)
    {
        int *Newspce = (int *)malloc(arr->cap * 2 * sizeof(int));
        memcpy(Newspce, arr->pAddr, arr->cap * sizeof(int));
        free(arr->pAddr);
        arr->cap = arr->cap * 2;
        arr->pAddr = Newspce;
    }
    arr->pAddr[arr->size] = value;
    arr->size++;
}

Output linear table elements from left to right.

void Printf_Array(ChaLenArray *arr) //Print
{
    if (arr == NULL)
        return;
    for (int i = 0; i < arr->size; i++)
    {
        /* code */
        printf("%d ", arr->pAddr[i]);
    }
    printf("\n");
}

3.2 variable length one-dimensional array

One dimensional array. Linear table elements exist in array[0,n-1]. To increase or decrease the length of this array, first create a new array, then copy array to this array, and finally change the value of array, which can reference the new array.

//c + + implementation
template <class T>
void ChangeLength1D(T *a, int OldLength, int NewLength)
{
    //if (NewLength <= 0)
    //    throw "new length must be >=0";
    T *temp = new T[NewLength];
    int number = min(OldLength, NewLength);
    copy(a, a + number, temp);
    delete[] temp;
    a = temp;
}
//C language implementation
ChaLenArray *Expand_Capacity(ChaLenArray *old_arr)
{
    if (old_arr == NULL)
        return NULL;
    ChaLenArray *New_arr;
    New_arr->cap = (int *)malloc(sizeof(int) * old_arr->cap * 2);
    memcpy(New_arr->pAddr, old_arr->pAddr, old_arr->cap * sizeof(int));
    New_arr->size = old_arr->size;
    free(old_arr->pAddr);
    return New_arr;
}

Chapter IV linear list - linked list

4.1 one way linked list

In chain description, each element of a data instance is described by a unit or node. The position of the element of the array does not need to be determined by the formula. Instead, each node explicitly contains the location information of another related node, which is called a link or pointer.

Generally speaking, in order to find the element whose index is theIndex, you need to start with firstNode and trace theIndex pointers to find it. Each node of the chain of a linear list has only one chain. This structure is called a singly linked list. From left to right in the linked list, each node (except the last node) is linked to the next node, and the chain field value of the last node is NULL. Such a structure is also called a chain.

Therefore, the data types are defined as follows:

//Define node
typedef struct LINKNODE
{
    void *data; //Pointer to any data (data field)
    struct LINKNODE *next;//Point to the next node (pointer field)
} LinkNode;
//Define linked list
typedef struct LINKLIST
{
    LinkNode *head;//Define header node
    int size;//Define linked list length
} LinKList;

Initialization: first, you need to initialize the linked list. For a linked list, you only need to initialize the pointer field and data field of the head node.

LinKList *Init_LinkList()
{
    LinKList *list = (LinKList *)malloc(sizeof(LinKList));//Application memory storage linked list
    list->size = 0;
    list->head = (LinkNode *)malloc(sizeof(LinkNode));//Request memory storage header node
    list->head->data = NULL;//Data field of head node
    list->head->next = NULL;//Pointer field of header node
}

Insert element: pass in the element to be inserted together with table List, position Pos and Data pointer Data. This insert_ The linklist() function inserts a meta cable after the position indicated by Pos. It means that there are no fully defined rules for how the insert operation is implemented. It is very possible to insert the new element into position Pos (i.e. in front of the element cable at that time at position P), so you need to know the element in front of position P.

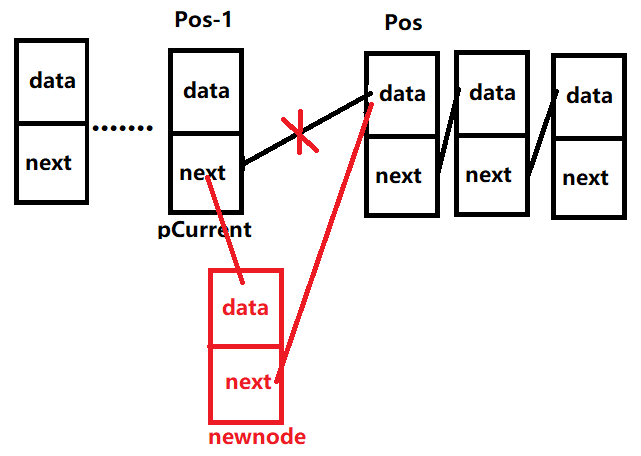
void Insert_LinkList(LinKList *List, int Pos, void *Data)
{
    if (list == NULL || data == NULL)
        return;
    if (pos < 0 || pos > list->size)
        pos = list->size;
    //Create a new node
    LinkNode *newNode = (LinkNode*)malloc(sizeof(LinkNode));
    newNode->data = data;
    newNode->next = NULL;
    //Find node (i.e. Pos-1 location)
    LinkNode *pCurrent = list->head; //Auxiliary pointer
    for (int i = 0; i < pos; i++)
    {
        pCurrent = pCurrent->next;
    }
    //New node into linked list
    newNode->next = pCurrent->next;
    pCurrent->next = newNode;
    list->size++;
}

Delete element: delete an element X in the table List by position. It is necessary to obtain the position of element x, which is the same as the insertion operation. Maybe find the previous element, cache the pointer field information of the previous element, and point the pointer field information to the next position of Pos.

void RemoveByBos_linkList(LinKList *list, int pos)
{
    if (list == NULL)
        return;
    if (pos < 0 || pos >= list->size)
        return;
    //Find the previous node deleted
    LinkNode *pCurrent = list->head;
    for (int i = 0; i < pos; i++)
    {
        pCurrent = pCurrent->next;
    }
    //Cache nodes to be deleted
    LinkNode *pDel = pCurrent->next;
    pCurrent->next = pDel->next->next;
    //Delete memory node release
    free(pDel);
    list->size--;
}

Find elements: find the specified data elements in the linked list. The most common method is to traverse the nodes in the table in turn from the header, and compare the found elements with the data elements stored in the data field of each node.

int Find_LinkList(LinKList *list, void *data)
{
    if (list == NULL || data == NULL)
        return -1;
    int i;
    LinkNode *pCurrent = list->head->next;
    while (pCurrent != NULL)
    {
        if (pCurrent->data == data)
        {
            break;
        }
        i++;
        pCurrent = pCurrent->next;
    }
    return i;
}

Printout: traverse all elements in the linked list until the last element is NULL. Here, in order to Print any type of data, the function pointer is used and the Print function is redefined.

void MyPrint(void *data)
{
    PERSON *p = (PERSON *)data;
    printf("Name:%s Age:%d Score:%d\n", p->name, p->age, p->score);
}

void Printf_LinkList(LinKList *list, PRINTFLINKNODE print)
{
    if (list == NULL)
        return;
    LinkNode *pCurrent = list->head->next;
    while (pCurrent != NULL)
    {
        print(pCurrent->data);
        pCurrent = pCurrent->next;
    }
}

Release linked list: empty the memory of all elements, including linked list and nodes.

void FreeSpace_LinkList(LinKList *list)
{
    if (list == NULL)
        return;
    LinkNode *pCurrent = list->head;
    while (pCurrent != NULL)
    {
        //Cache next node
        LinkNode *pNext = pCurrent->next;
        free(pCurrent);
        pCurrent = pNext;
    }
    list->size = 0;
    free(list);
}

4.2 bidirectional linked list

Although the use of single linked list can 100% solve the storage problem of data whose logical relationship is "one-to-one", single linked list is not the most efficient storage structure when solving some special problems. For example, if the algorithm needs to find a large number of forward nodes of a specified node, using a single linked list is undoubtedly disastrous, because the single linked list is more suitable for "looking from front to back", and "looking from back to front" is not its strength. In this section, learn about the two-way linked list (double linked list for short).

Bidirectional means that the logical relationship between nodes is bidirectional, but usually only one header pointer is set, unless required by the actual situation.

As can be seen from the above figure, each node in the two-way linked list contains the following three parts of information:

Pointer field: used to point to the direct precursor node of the current node;
Data field: used to store data elements.
Pointer field: used to point to the direct successor node of the current node;

Data type:

typedef int NodeDataType;
typedef struct _DoublelinkedNode
{
    struct _DoublelinkedNOde *prior; //Direct forward trend
    NodeDataType data;
    struct _DoublelinkedNode *next; //Direct successor
} DoubLinkNode;

Initialize a two-way linked list:

DoubLinkNode *DoubListInit()
{
    DoubLinkNode *head = (DoubLinkNode *)malloc(sizeof(DoubLinkNode));
    head->prior = NULL;
    head->next = NULL;
    head->data = 1;
    //Declare a pointer to the initial node to facilitate the later addition of newly created nodes to the linked list
    DoubLinkNode *list = head;
    for (int i = 2; i <= 5; i++)
    {
        //Create a new node and initialize it
        DoubLinkNode *body = (DoubLinkNode *)malloc(sizeof(DoubLinkNode));
        body->prior = NULL;
        body->next = NULL;
        body->data = i;
        //The new node establishes a relationship with the last node in the linked list
        list->next = body;
        body->prior = list;
        //List always points to the last node in the linked list
        list = list->next;
    }
    return head;
}

Adding nodes to a two-way linked list: there are three cases: head insertion, middle insertion and tail insertion.

1. Header insertion: to add a new data element to the header, you only need to establish a double-layer logical relationship between the element and the header element.

In other words, assuming that the new element node is temp and the header node is head, you need to do the following two steps:

temp->next=head; head->prior=temp;
Move the head to temp and point to the new header again;

2. Middle position insertion: the same as Single linked list Similar to adding data, adding data in the middle of a two-way linked list requires the following two steps,

The new node first establishes a two-tier logical relationship with its direct successor nodes;
The direct precursor node of the new node establishes a two-level logical relationship with it;

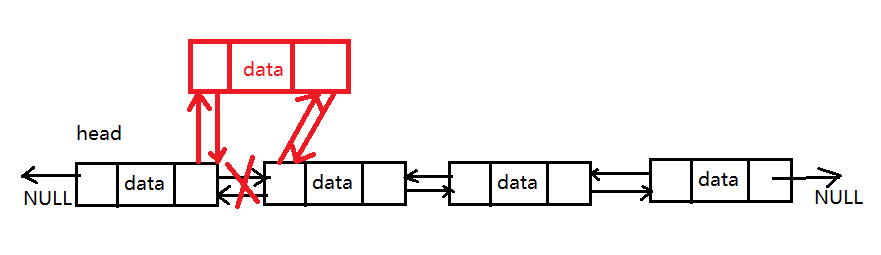
3. Tail insertion: it is the same as adding to the header. The implementation process is as follows:

Find the last node in the double linked list;
Make the new node and the last node have a double-layer logical relationship;

[the external link image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-7y6OSqPT-1622084567131)(D: \ Xiaozhou's tribal Pavilion \ DataStructAndAlgorithms \ bidirectional linked list footer. png)]

DoubLinkNode *InsertList(DoubLinkNode *list, NodeDataType data, int pos)
{
    DoubLinkNode *NewNode = (DoubLinkNode *)malloc(sizeof(DoubLinkNode));
    NewNode->data = data;
    NewNode->next = NULL;
    NewNode->prior = NULL;
    //Special consideration should be given to inserting into the chain header
    if (pos == 1)
    {
        NewNode->next = list;
        list->prior = NewNode;
        list = NewNode;
    }
    //Insert into linked list
    else
    {
        DoubLinkNode *pCurrent = list; //Auxiliary pointer to find the previous node of the insertion position
        for (int i = 0; i < pos - 1; i++)
        {
            pCurrent = pCurrent->next;
        }
        if (pCurrent->next == NULL) //Note the insertion point is the tail
        {
            pCurrent->next = NewNode;
            NewNode->prior = pCurrent;
        }
        else //Indicates that the insertion point is in the middle
        {
            pCurrent->next->prior = NewNode;
            NewNode->next = pCurrent->next;
            pCurrent->next = NewNode;
            NewNode->prior = pCurrent;
        }
    }
    return list;
}

Bidirectional linked list delete node: when deleting a node from a double linked list, you only need to traverse the linked list to find the node to be deleted, and then remove the node from the list.

DoubLinkNode *DeleteNodeByData(DoubLinkNode *list, int data)
{
    if (list == NULL)
        return -1;
    DoubLinkNode *pCurrent = list;
    while (pCurrent)
    {
        if (pCurrent->data == data)
        {

            pCurrent->next->prior = pCurrent->prior;
            //pCurrent->prior->next = pCurrent->next;
            free(pCurrent);
            return list;
        }
        pCurrent = pCurrent->next;
    }
    printf("tThis list doesn't have this element\n");
    return list;
}

Two way linked list lookup node: usually, two-way linked lists, like single linked lists, have only one header pointer. Therefore, the implementation of finding the specified elements in the double linked list is similar to that in the single linked list, which traverses the elements in the list in turn from the header.

NodeDataType selectElem(DoubLinkNode *list, NodeDataType elem)
{
    //Create a new pointer t and initialize it as the head pointer head
    DoubLinkNode *t = list;
    int i = 1;
    while (t)
    {
        if (t->data == elem)
        {
            return i;
        }
        i++;
        t = t->next;
    }
    //If the program executes here, the search fails
    return -1;
}

Two way linked list change node: the operation of changing the specified node data field in the double linked list is completed on the basis of search. The implementation process is: find the node storing the data element through traversal, and directly change its data field.

//Update function, where add means to change the position of the node in the double linked list, and newElem is the value of the new data
DoubLinkNode *amendElem(DoubLinkNode *list, int pos, int newElem)
{
    DoubLinkNode *temp = list;
    //Traverse to the deleted node
    for (int i = 1; i < pos; i++)
    {
        temp = temp->next;
    }
    temp->data = newElem;
    return list;
}

4.3 classic algorithm problem - Joseph Ring

Joseph's ring problem is a classic circular linked list problem. The meaning of the question is: it is known that n individuals (represented by numbers 1, 2, 3,..., n respectively) sit around a round table, count clockwise from the person numbered k, and the person counted to m is listed; His next person starts from 1 again, or starts counting clockwise, and the person who counts to m is listed again; Repeat until there is one person left on the round table.

As shown in the figure, assuming that there are 5 people around the circumference at this time, it is required to count clockwise from the person numbered 3, and the person counted to 2 is listed:

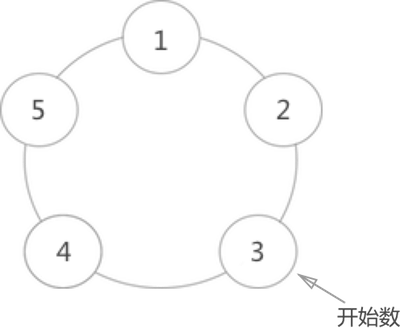
The order of listing is as follows:

The person with number 3 starts counting 1, and then 4 counts 2, so 4 comes out first;
After 4 is out of the train, count 1 from 5, and 1 counts 2, so 1 is out of the train;
After 1 is out of the train, count 1 from 2, and 3 counts 2, so 3 is out of the train;
After 3 is out of the train, count 1 from 5 and 2 from 2, so 2 is out of the train;
In the end, there were only 5 of them, so 5 won.

It is possible to use the linked list method to simulate this process. N individuals are regarded as n linked list nodes. Node 1 points to node 2, node 2 points to node 3,..., node N-1 points to node n, and node n points to node 1. In this way, a ring is formed. Then start from node 1, 1, 2, 3... And count down. Every time M is checked in, the node is deleted from the ring. The next node then starts counting from 1. Finally, there is only one node left in the linked list. It is the ultimate winner.

Disadvantages: to simulate the whole game process, the time complexity is as high as O(nm). When n and m are very large (for example, millions, tens of millions), there is almost no way to produce results in a short time.

#include <stdio.h>
#include <stdlib.h>
typedef struct node{
    int number;
    struct node * next;
}person;
person * initLink(int n){
    person * head=(person*)malloc(sizeof(person));
    head->number=1;
    head->next=NULL;
    person * cyclic=head;
    for (int i=2; i<=n; i++) {
        person * body=(person*)malloc(sizeof(person));
        body->number=i;
        body->next=NULL; 
        cyclic->next=body;
        cyclic=cyclic->next;
    }
    cyclic->next=head;//end to end
    return head;
}

void findAndKillK(person * head,int k,int m){
 
    person * tail=head;
    //Find the previous node of the first node in the linked list to prepare for the deletion operation
    while (tail->next!=head) {
        tail=tail->next;
    }
    person * p=head;
    //Find the person with number k
    while (p->number!=k) {
        tail=p;
        p=p->next;
    }
    //Starting from the person with number k, only when p - > next = = P is met, it indicates that all numbers in the linked list are listed except for node P,
    while (p->next!=p) {
        //Find the person who reports m from p to 1, and also know the location tail of the number of m-1de people, so as to facilitate the deletion operation.
        for (int i=1; i<m; i++) {
            tail=p;
            p=p->next;
        }
        tail->next=p->next;//Remove the p node from the linked list
        printf("Listed by number:%d\n",p->number);
        free(p);
        p=tail->next;//Continue to use the p pointer to point to the next number of the column number, and the game continues
    }
    printf("The number of the listed person is:%d\n",p->number);
    free(p);
}

int main() {
    printf("Enter the number of people on the round table n:");
    int n;
    scanf("%d",&n);
    person * head=initLink(n);
    printf("From the first k People began to count off(k>1 And k<%d): ",n);
    int k;
    scanf("%d",&k);
    printf("Count to m List of people:");
    int m;
    scanf("%d",&m);
    findAndKillK(head, k, m);
    return 0;
}

Chapter 5 stack and queue

4.1 stack

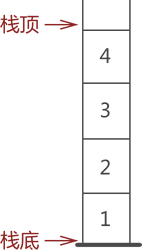
Like sequential list and linked list, stack is also a linear storage structure used to store "one-to-one" data with logical relationship, as shown in the figure.

[the external link image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-b0e0CuPG-1622084567140)(D: \ Xiaozhou's tribal Pavilion \ DataStructAndAlgorithms \ stack png.png)]
As can be seen from the figure, the stack storage structure is different from the linear storage structure learned before. This is because the stack has special requirements for the process of "saving" and "fetching" data:

The stack can only access data from one end of the table, and the other end is closed;
In the stack, whether storing or fetching data, we must follow the principle of "first in and last out", that is, the first element in the stack is the last one out of the stack. Judging from the storage state of the data in the figure, element 1 is the most advanced stack. Therefore, when element 1 needs to be taken out of the stack, according to the principle of "first in, last out", element 3 and element 2 need to be taken out of the stack in advance, and then element 1 can be successfully taken out.

Therefore, stack is a linear storage structure that can only access data from one end of the table and follows the "first in, last out" principle.

The open end of the stack is called the top of the stack; Accordingly, the sealing end is called the bottom of the stack. Therefore, the stack top element refers to the element closest to the stack top. Take Figure 2 for example, the stack top element is element 4; Similarly, the element at the bottom of the stack refers to the element at the bottom of the stack. The element at the bottom of the stack in the figure is element 1.

4.2 stacking in and out

Based on the characteristics of stack structure, in practical application, only the following two operations are usually performed on the stack:

Adding elements to the stack is called "stacking" (stacking or pressing);
Extracting the specified element from the stack is called "out of stack" (or pop stack);

Stack is a "special" linear storage structure. Therefore, there are two ways to realize stack:

Sequential stack: the sequential storage structure can simulate the characteristics of stack storage data, so as to realize the stack storage structure;

//Data structure of stack
typedef int dataType;
typedef struct _LinearStack
{
    dataType arr[MAX_SIZE];
    int size;
} LinearStack;

//Initialize a stack:
LinearStack *StackInit()
{
    LinearStack *stack = (LinearStack *)malloc(sizeof(LinearStack));
    for (int i = 0; i < MAX_SIZE; i++)
        stack->arr[i] = 0;
    stack->size = 0;
    return stack;
}

//Push 
LinearStack *PushStack(LinearStack *stack, dataType data)
{
    stack->arr[stack->size] = data;
    printf("data:%d Press into the stack at:%d \n", stack->arr[stack->size], stack->size);
    stack->size++;
    return stack;
}
//Out of stack
LinearStack *PopStack(LinearStack *stack)
{

    printf("data:%d Out of stack", stack->arr[stack->size]);
    stack->arr[stack->size] = 0;
    stack->size--;
    printf("The remaining stack length is:%d \n", stack->size);
    return stack;
}

4.3 queue

Different from the stack structure, both ends of the queue are "open", which requires that data can only enter from one end and exit from the other end, as shown in the figure:

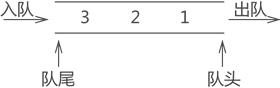
Generally, one end of incoming data is called "queue tail", one end of outgoing data is called "queue head", the process of data elements entering the queue is called "queue in", and the process of data elements leaving the queue is called "queue out".

Stack and queue should not be confused. The stack structure is sealed at one end, which is characterized by "first in and last out"; Both ends of the queue are full of openings, which are characterized by "first in, first out".

4.4 joining and leaving the team

Because the bottom layer of the sequential queue uses arrays, it is necessary to apply for a large enough memory space to initialize the sequential queue in advance. In addition, in order to meet the requirements of data in the sequential queue from the end of the queue, the first out of the queue and first in first out.

typedef int datatype;
typedef struct _Queue
{
    datatype arr[MAX];
    int size;
} Queue;
Queue *QueueInit()
{
    Queue *queue = (Queue *)malloc(sizeof(queue));
    for (int i = 0; i < MAX; i++)
    {
        queue->arr[i] = NULL;
    }
    queue->size = 0;
}
void PushQueue(Queue *queue, datatype data)
{
    if (queue == NULL || queue->size == MAX)
    {
        return;
    }
    queue->arr[queue->size] = data;
    queue->size++;
}
void PopQueue(Queue *queue)
{
    if (queue == NULL || queue->size == MAX)
    {
        return;
    }
    for (int i = 0; i < queue->size - 1; i++)
    {
        queue->arr[i] = queue->arr[i + 1];
    }
    queue->size--;
}
datatype BackTopQueue(Queue *queue)
{
    if (queue == NULL || queue->size == MAX)
    {
        return;
    }
    return queue->arr[queue->size];
}

4.5 application of stack and queue

Based on the characteristics of "first in, last out" principle for data access based on stack structure, it can be used to realize many functions.

For example, we often use browsers to find information on various websites. Suppose you browse page a first, then close page A and jump to page B, and then close page B and jump to page C. At this time, if we want to return to page a, we have two choices:

Search again to find page A;
Use the browser's fallback function. The browser will first go back to page B and then back to page A.

The bottom layer of the browser's "fallback" function is the stack storage structure. When you close page A, the browser will put page A on the stack; Similarly, when you close page B, the browser will put B on the stack. Therefore, when you perform the fallback operation, you will first see page B and then page A, which is the effect of the data in the stack coming out of the stack in turn.

Moreover, the stack storage structure can also help us detect the bracket matching problem in the code. Most programming languages use parentheses (small parentheses, square brackets and curly braces). The wrong use of parentheses (usually missing right parentheses) will lead to program compilation errors. Many development tools have the function of detecting whether the code has editing errors, including detecting the matching of parentheses in the code. The underlying implementation of this function uses the stack structure.

At the same time, the stack structure can also realize the hexadecimal conversion of values. For example, writing a program to automatically convert decimal numbers into binary numbers can be realized by using stack storage structure.

The above is only the tip of the iceberg in the field of stack applications. There are no more examples here. In the following chapters, we will use a lot of stack structure. Next, we will learn how to implement sequential stack and chain stack, and how to input and output the elements in the stack.

Chapter VI string

In the data structure, the string should be stored separately with a storage structure, which is called string storage structure. The string here refers to the string. Strictly speaking, the string storage structure is also a linear storage structure, because the characters in the string also have a "one-to-one" logical relationship. The string structure used to store data is different from the previous linear structure.

No matter which programming language you learn, the string is always the most operated. In the data structure, some special strings are named according to the number and characteristics of characters stored in the string, such as:

Empty string: a string that stores 0 characters, such as S = "" (double quotation marks next to each other);
Space string: a string containing only space characters, such as S = "" (double quotation marks contain 5 spaces);
Substring and main string: suppose there are two strings a and b. if the string composed of several consecutive characters can be found in a is exactly the same as b, then a is the main string of b and b is the substring of A. For example, if a = "shujujiegou", b = "shuju", because a also contains "shuju", string a and string b are the relationship between the main string and the sub string;

In addition, for two strings with the relationship between main string and sub string, you will usually use the algorithm to find the position of the sub string in the main string. The position of the substring in the main string refers to the position of the first character of the substring in the main string.

For example, string a = "shujujiegou", string b = "jiegou", through observation, it can be judged that a and b are the relationship between the main string and sub string, and sub string b is located at the 6th position in main string a, because in string a, the position of the first character 'j' of string b is 6.

6.1 fixed length sequential storage of strings

The fixed length sequential storage structure of strings can be simply understood as using "fixed length sequential storage structure" to store strings, so it is limited that its underlying implementation can only use static arrays.

When using the fixed length sequential storage structure to store strings, it is necessary to apply for enough memory space in advance in combination with the length of the target string. For example, the fixed length sequential storage structure is used to store "www.codezou. Club". Through visual inspection, it is known that the length of this string is 17, so the length of the array space we apply for is at least 18 (the end flag '\ 0' of the last stored string), which is expressed in C language as follows:

char str[18] = "www.codezhou.club";

6.2 heap allocation storage of string

The heap allocation storage of string is realized by using dynamic array to store string. Usually, the programming language will divide the memory space occupied by the program into several different areas, and the data contained in the program will be classified and stored in the corresponding area. Take C language for example. The program will divide the memory into four areas: heap area, stack area, data area and code area.

Different from other areas, the memory space in the heap area needs to be applied for manually by the programmer using malloc function, and it needs to be released manually through the free function after it is not used.

The scene where malloc function is most used in C language is to allocate space to arrays, which are called dynamic arrays. For example:

char * a = (char*)malloc(5*sizeof(char));

This line of code creates a dynamic array A and applies for heap storage space of 5 char types by using malloc.

The advantage of dynamic array over ordinary array (static array) is that the length is variable. In other words, dynamic array can apply for more heap space as needed (use the relloc function):

a = (char*)realloc(a, 10*sizeof(char));

By using this line of code, the dynamic array with 5 char storage spaces can be expanded to store 10 char data.

The complete display is as follows:

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main()
{
    char *a1 = NULL;
    char *a2 = NULL;
    a1 = (char *)malloc(10 * sizeof(char));
    strcpy(a1, "http://Www "); / / string" http://www Copy to a1
    a2 = (char *)malloc(10 * sizeof(char));
    strcpy(a2, "codezhou.club");
    int lengthA1 = strlen(a1); //a1 length of string
    int lengthA2 = strlen(a2); //a2 length of string
    //Try to store the merged string in a1. If there is not enough space in a1, use realloc to apply dynamically
    if (lengthA1 < lengthA1 + lengthA2)
    {
        a1 = (char *)realloc(a1, (lengthA1 + lengthA2 + 1) * sizeof(char));
    }
    //Merge two strings into a1
    for (int i = lengthA1; i < lengthA1 + lengthA2; i++)
    {
        a1[i] = a2[i - lengthA1];
    }
    //Add \ 0 to the end of the string to avoid errors
    a1[lengthA1 + lengthA2] = '\0';
    printf("%s", a1);
    //Dynamic array to be released immediately
    free(a1);
    free(a2);
    return 0;
}

6.3 BF algorithm

Brute force algorithm is an ordinary pattern matching algorithm. The idea of BF algorithm is to match the first character of target string S with the first character of pattern string T. if they are equal, continue to compare the second character of S with the second character of T; If they are not equal, compare the second character of S with the first character of T, and compare them successively until the final matching result is obtained. BF algorithm is a brute force algorithm.

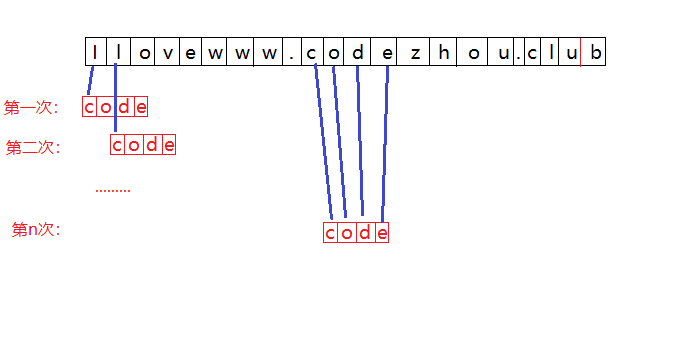
int index( String S, String T, int pos )
{
    int i = pos;                        // i indicates the subscript of the current position in the main string S
    int j = 1;                            // j represents the current position subscript in substring T
    while( i <= S[0] && j <= T[0] ){    // If one of i or j reaches the tail, the search is terminated
        if( S[i] == T[i] ){             // If equal, continue with the next element match
            i++;
            j++;
        }
        else {                         // If the match fails, j backtrack to the first element to rematch
            i = i - j + 2;              // Retrace i to the next element in the first place of the last match
            j = 1;
        }
    }
    if( j > T[0] ){
        return i - T[0];
    }
    else {
        return 0;
    }
}

Time complexity of BF algorithm: the optimal time complexity of the algorithm is O(n). N represents the length of string A, that is, the first matching is successful. The worst-case time complexity of BF algorithm is O(n*m), n is the length of string A and M is the length of string B. For example, string B is "0000000001" and string A is "01". In this case, each time the two strings match, they must match to the end of string A to judge the matching failure. Therefore, it runs n*m times.

The implementation process of BF algorithm is "mindless" and does not contain any skills. When pattern matching a string with a large amount of data, the efficiency of the algorithm is very low.

6.4 KMP algorithm

stay computer science Knuth Morris Pratt String lookup algorithm (referred to as KMP algorithm for short) can be in one character string Find the position of a word W in S. When a word does not match, it itself contains enough information to determine the possible starting position of the next match. This algorithm uses this feature to avoid rechecking the previous match character.

This algorithm consists of Gartner and Vaughan Pratt Conceived in 1974, the same year James H. Morris The algorithm was also designed independently, and finally jointly published by the three in 1977.

Topics: Algorithm linked list

Programmer Think