Basic sorting: bubble sorting, selection sorting and insertion sorting. In the worst case, the time complexity is O(N^2), square order. With the increase of input scale, the time cost will rise sharply, so these basic sorting methods can not deal with larger scale problems

4.1 Hill sorting

Hill sort is a kind of insertion sort, also known as "reduced incremental sort", which is a more efficient improved version of insertion sort algorithm

Case:

• Requirements: before sorting: {9,1,2,5,7,4,8,6,3,5} after sorting: {1,2,3,4,5,5,6,7,8,9}

• Sorting principle

  1. Select a growth amount h and group the data according to the growth amount h as the basis for data grouping

  2. Insert and sort each group of data divided into groups

  3. Reduce the growth to 1 and repeat the second step

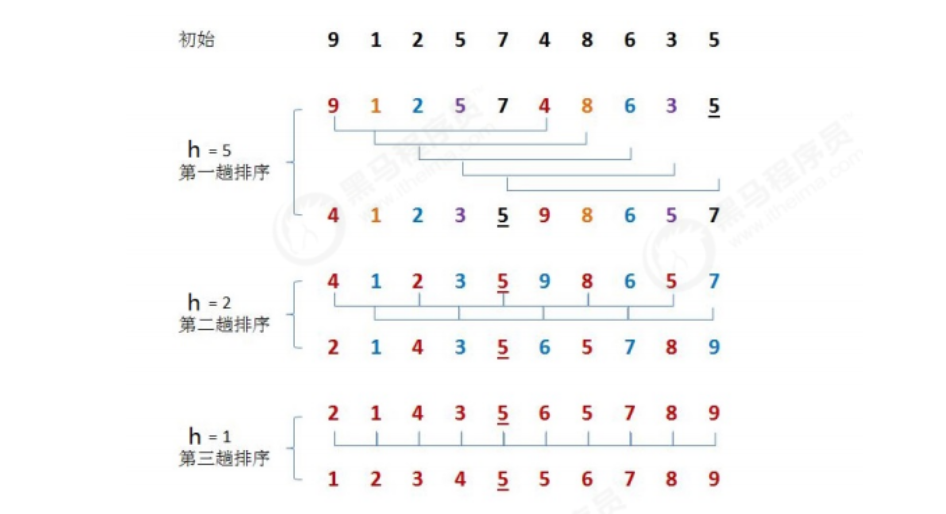
• Growth h rule

// Determine the maximum value of growth h
int h = 1
while(h < Array length/2){
	h = 2h + 1；
}


// Reduction rule of growth h
h = h/2

• API design

• code implementation

public class ShellSort {
    /**
     * Shell Sort 
     *
     * @param c
     */
    public static void sort(Comparable[] c) {
        // 1. The initial value of the growth amount h is determined according to the length of the array c
        int h = 1;
        while (h < c.length / 2) {
            h = 2 * h + 1;
        }

        // 2. Hill sort
        while (h > 0) {
            // 2.1. Find the element to be inserted
            for (int i = h; i < c.length; i++) {
                // 2.2 place the elements to be inserted in the appropriate position
                for (int j = i; j >= h; j -= h) {
                    // The element to be inserted is c[j]; Compare c[j], c[j-h]
                    if (greater(c[j - h], c[j])) {
                        //The front is larger than the back, swap positions
                        exch(c, j - h, j);
                    } else {
                        // If the front is not greater than the rear, exit the inner loop
                        break;
                    }
                }
            }

            // 2.3 reduce the h value and continue the next cycle
            h = h / 2;
        }
    }

    /**
     * Compare whether c1 is greater than c2
     *
     * @param c1
     * @param c2
     * @return
     */
    private static boolean greater(Comparable c1, Comparable c2) {
        return c1.compareTo(c2) > 0;
    }

    /**
     * Replace the elements at positions i and j in array c
     *
     * @param c
     * @param i
     * @param j
     */
    private static void exch(Comparable[] c, int i, int j) {
        Comparable temp = c[i];
        c[i] = c[j];
        c[j] = temp;
    }
}

public class SortTest {
    /**
     * Shell Sort 
     */
    @Test
    public void testShellSort(){
        Integer[] c = {9,1,2,5,7,4,8,6,3,5};
        System.out.println("Before sorting:" + Arrays.toString(c));
        ShellSort.sort(c);
        System.out.println("After sorting:" + Arrays.toString(c));
    }
}

Before sorting:[9, 1, 2, 5, 7, 4, 8, 6, 3, 5]
After sorting:[1, 2, 3, 4, 5, 5, 6, 7, 8, 9]

• Time complexity analysis

  In Hill sort, there is no fixed rule for growth h, so we won't analyze it here.
  Post hoc analysis can be used to compare the performance of Hill sort and insert sort.

• performance testing

  The reverse data from 100000 to 1 can be used to complete the test according to this batch data.

  Test idea: record the time difference before and after sorting

public class SortTest {
    /**
     * Compare insert sort and Hill sort
     */
    @Test
    public void testInsertionAndShell() {
        Integer[] c = getArray(10_0000);
        long start = System.currentTimeMillis();
        //InsertionSort.sort(c);// Time: 17683
        ShellSort.sort(c);//Time: 27
        long end = System.currentTimeMillis();
        System.out.println("Time:" + (end - start));
    }

    /**
     * Get the array to be sorted
     * Worst case (in reverse order, from large to small)
     *
     * @param n
     * @return
     */
    private Integer[] getArray(int n) {
        Integer[] c = new Integer[n];
        for (int i = 0; i < n; i++) {
            c[i] = n - i;
        }
        return c;
    }
}

Insert sort time: 17683
 Hill sorting time: 27  

Through the test, it is found that the performance of Hill sort is significantly higher than that of insert sort when dealing with large quantities of data

4.2 merging and sorting

1) Recursion

• Definition: when defining a method, the method itself is called inside the method, which is called recursion

public void show(){
    System.out.println("aaaa");
    show();
}

• effect
  It usually transforms a large and complex problem into a smaller problem similar to the original problem. The recursive strategy only needs a small number of programs, which can describe the multiple repeated calculations required in the problem-solving process, which greatly reduces the amount of code of the program
• matters needing attention
  In recursion, you can't call yourself unlimited. You must have boundary conditions to end the recursion, because each recursive call will open up a new space in the stack memory and re execute the method. If the recursion level is too deep, it is easy to cause stack memory overflow

2) Merge sort

Merge sort is an effective sort algorithm based on merge operation. This algorithm is a very typical application of divide and conquer method. The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called two-way merging

Case:

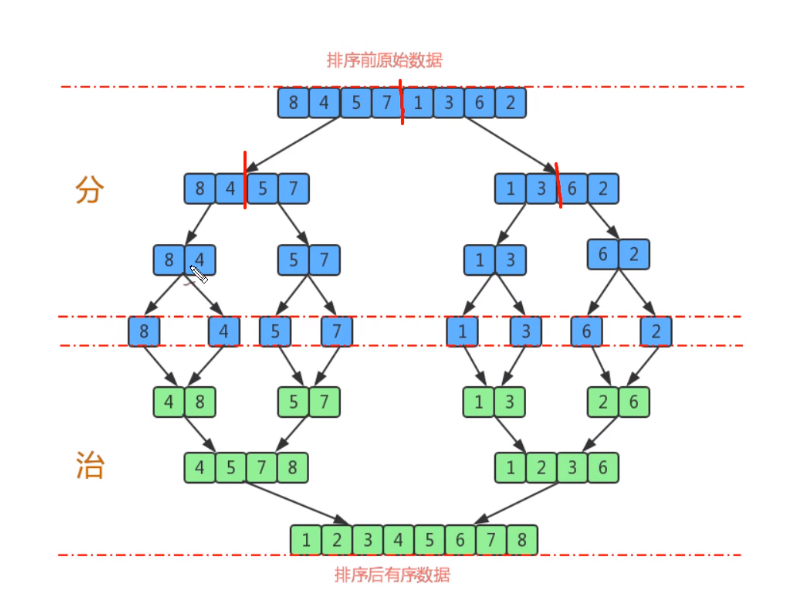
• **Requirements: * * before sorting: {8,4,5,7,1,3,6,2} after sorting: {1,2,3,4,5,6,7,8}

• Sorting principle

  1. Split a set of data into two subgroups with equal elements as far as possible, and continue to split each subgroup until the number of elements in each subgroup is 1

  2. Merge two adjacent subgroups into an ordered large group

  3. Repeat step 2 until there is only one group

• API design

• Merging principle

• code implementation

public class MergeSort {
    /**
     * Auxiliary array required for merging
     */
    private static Comparable[] assist;

    /**
     * Sort the elements in array c
     *
     * @param c
     */
    public static void sort(Comparable[] c) {
        // 1. Initialize auxiliary array
        assist = new Comparable[c.length];

        // 2. Define variables lo and hi; Record the boundary index in the array separately
        int lo = 0;
        int hi = c.length - 1;

        // 3. Call the sort overloaded method to complete the sorting from lo to hi in array c
        sort(c, lo, hi);
    }

    /**
     * Sort the elements from lo to hi in array c
     *
     * @param c
     * @param lo
     * @param hi
     */
    private static void sort(Comparable[] c, int lo, int hi) {
        // 1. Parameter validity check
        if (hi <= lo) {
            return;
        }

        // 2. Group from lo to hi in array c (two groups)
        int mid = lo + (hi - lo) / 2;

        // 3. Sort the two groups separately
        sort(c, lo, mid);
        sort(c, mid + 1, hi);

        // 4. Merge two groups
        merge(c, lo, mid, hi);
    }

    /**
     * In array c, from lo to mid is a group, and from mid+1 to hi is a group. Merge the two groups of data
     *
     * @param c
     * @param lo
     * @param mid
     * @param hi
     */
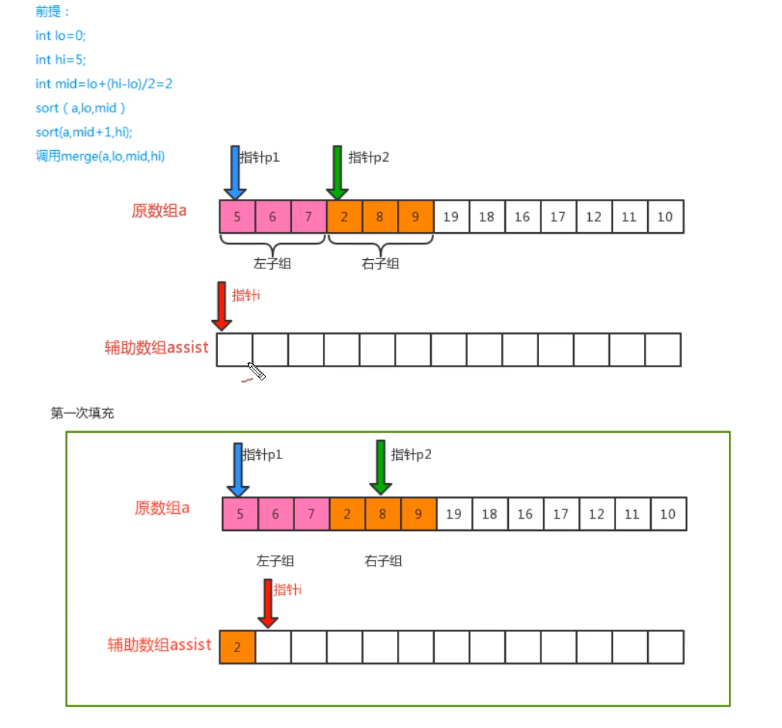
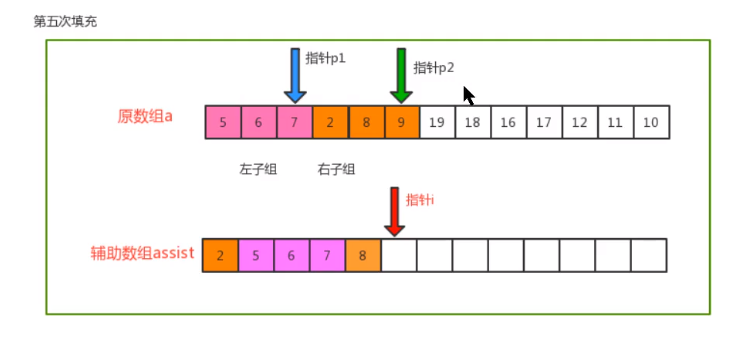
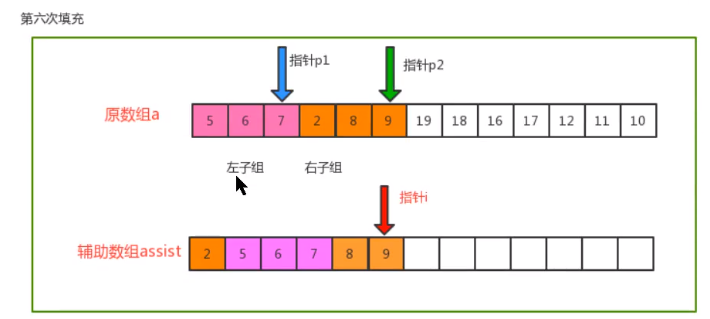
    private static void merge(Comparable[] c, int lo, int mid, int hi) {
        // Define three pointers: auxiliary array i, left sub array p1 and right sub array p2
        int i = lo;
        int p1 = lo;
        int p2 = mid + 1;

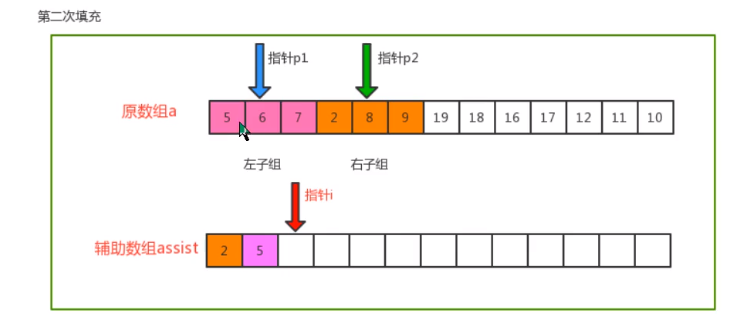
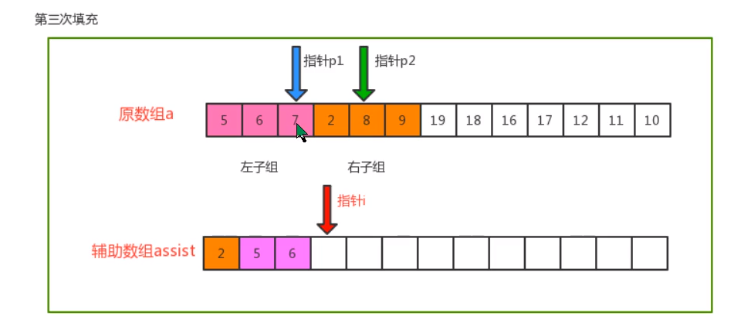
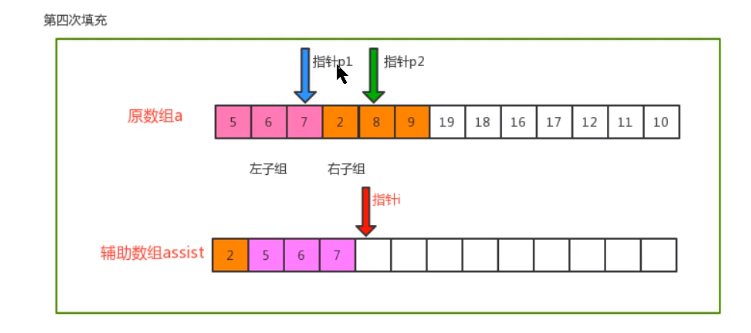
        // Traversal: move p1 and p2, compare the value of the index position, find out the small value, and put it into the corresponding position in the auxiliary array
        while (p1 <= mid && p2 <= hi) {
            if (less(c[p1], c[p2])) {
                assist[i++] = c[p1++];
            } else {
                assist[i++] = c[p2++];
            }
        }

        // Traversal: if the p1 pointer is not completed, move p1 sequentially and put the remaining elements into the corresponding position of the auxiliary array
        while (p1 <= mid) {
            assist[i++] = c[p1++];
        }

        // Traversal: if the p2 pointer is not completed, move p2 sequentially and put the remaining elements into the corresponding position of the auxiliary array
        while (p2 <= hi) {
            assist[i++] = c[p2++];
        }

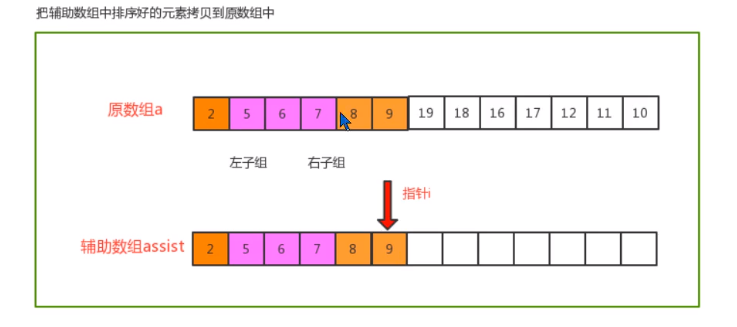
        // Copy the elements in the auxiliary array to the corresponding position in the original array
        for (int index = lo; index <= hi; index++) {
            c[index] = assist[index];
        }
    }

    /**
     * Compare whether c1 is less than c2
     *
     * @param c1
     * @param c2
     */
    private static boolean less(Comparable c1, Comparable c2) {
        return c1.compareTo(c2) < 0;
    }
}

public class SortTest {
    /**
     * Merge sort
     */
    @Test
    public void testMergeSort(){
        Integer[] c = {8,4,5,7,1,3,6,2};
        System.out.println("Before sorting:" + Arrays.toString(c));
        MergeSort.sort(c);
        System.out.println("After sorting:" + Arrays.toString(c));
    }
}

Before sorting:[8, 4, 5, 7, 1, 3, 6, 2]
After sorting:[1, 2, 3, 4, 5, 6, 7, 8]

• Time complexity analysis

  Merge sort is the most typical example of divide and conquer. In the above algorithm, a[lo... hi] is sorted and divided into a[lo... mid] and
  a[mid+1... hi] two parts, sort them separately through recursive calls, and finally merge the ordered sub arrays into the final sorting result. The exit of this recursion is that if an array can no longer be divided into two sub arrays, merge will be executed to determine the size of the elements and sort them when merging

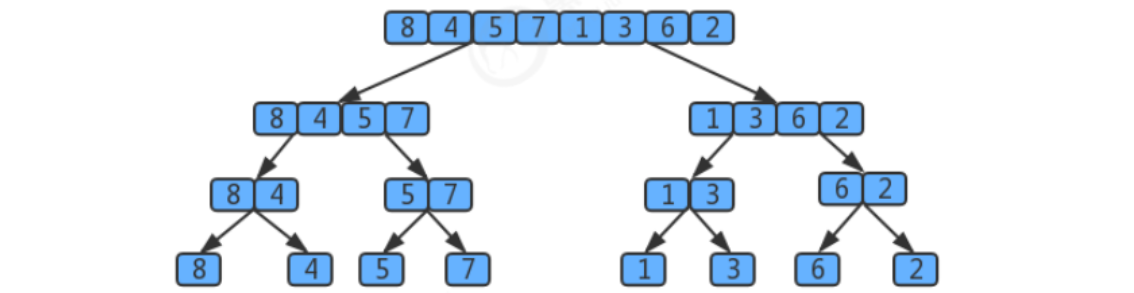
Use the tree view to describe merging. If an array has 8 elements, it will divide by 2 to find the smallest sub array every time. It will be disassembled for 8 times and the value is 3. Therefore, the tree has 3 layers. There are 2^k sub arrays from the top to the k layer, and the length of each array is 2^(3-k). Merging requires 2^(3-k) comparisons at most. Therefore, the comparison times of each layer is 2^k * 2^(3-k) = 2^3, so the total number of three layers is 3 * 2 ^ 3

Assuming that the number of elements is n, the number of splits using merge sort is log2(n), so there are log2(n) layers in total. Then, use log2(n) to replace the number of layers in 3 * 2 ^ 3 above. The time complexity of merge sort is: log2(n) * 2^(log2(n)) = log2(n) * n

According to the large o derivation rule, ignoring the base, the time complexity of the final merging and sorting is O(n*logn) (logarithmic order)

• shortcoming

  Additional array space needs to be applied, resulting in increased space complexity. It is a typical space for time operation

• Merge sort and Hill sort performance test

public class SortTest {
    /**
     * Compare Hill sort and merge sort
     */
    @Test
    public void testMergeAndShell(){
        Integer[] c = getArray(10_0000);
        long start = System.currentTimeMillis();
        //ShellSort.sort(c);// Time: 23
        MergeSort.sort(c);//Time: 52
        long end = System.currentTimeMillis();
        System.out.println("Time:" + (end - start));
    }

    /**
     * Get the array to be sorted
     * Worst case (in reverse order, from large to small)
     *
     * @param n
     * @return
     */
    private Integer[] getArray(int n) {
        Integer[] c = new Integer[n];
        for (int i = 0; i < n; i++) {
            c[i] = n - i;
        }
        return c;
    }
}

Through the test, it is found that Hill sort and merge sort are not very different in processing large quantities of data

4.3 quick sort

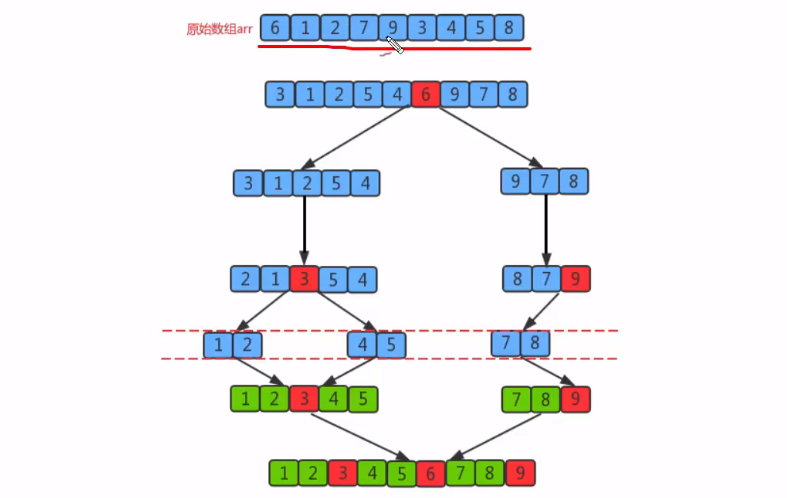
Quick sort is an improvement of bubble sort. Its basic idea is to divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so as to turn the whole data into an ordered sequence

Case:

• Requirements: before sorting: {6, 1, 2, 7, 9, 3, 4, 5, 8} after sorting: {1, 2, 3, 4, 5, 6, 7, 8, 9}

• Sorting principle

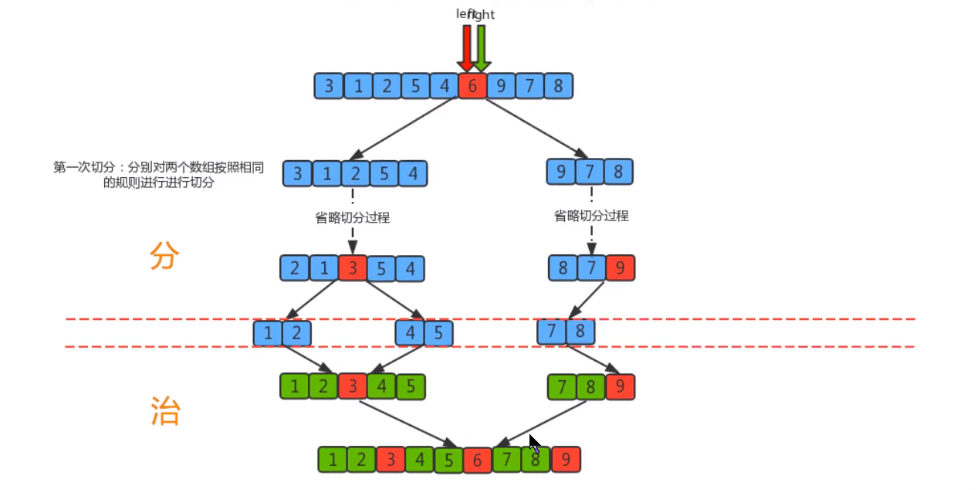
  1. First, set a boundary value, and divide the array into left and right parts through the boundary value

  2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value

  3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly

  4. By repeating the above process, we can see that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed

• API design

• Segmentation principle
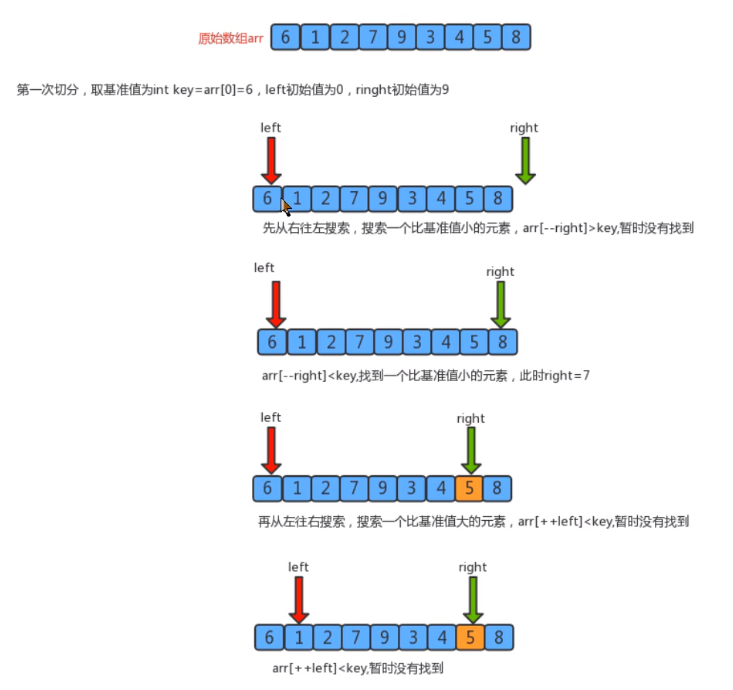
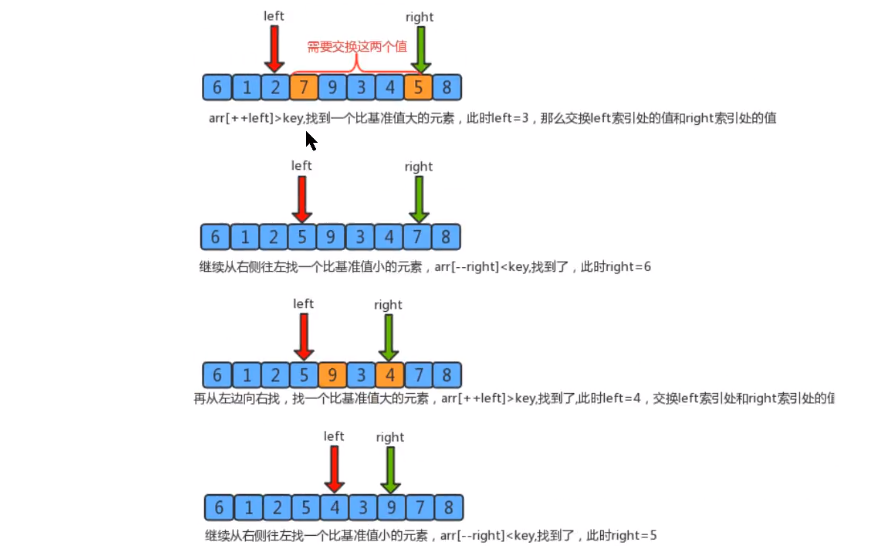
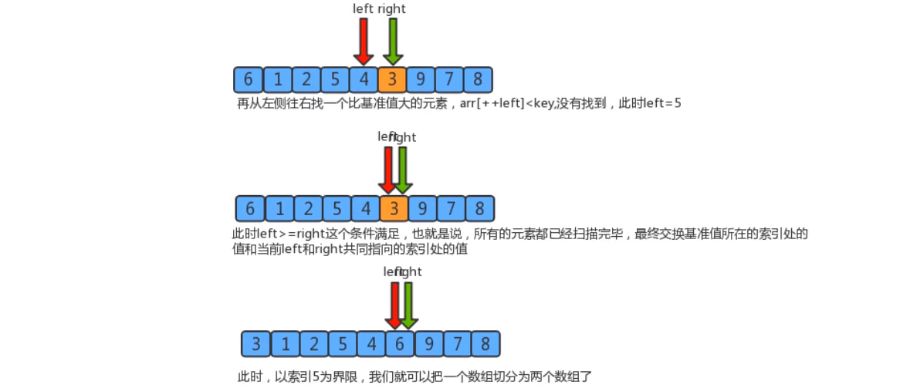
  The basic idea of dividing an array into two subarrays:
  1. Find a reference value and point to the head and tail of the array with two pointers
  2. Start from the tail to the head, search for an element smaller than the reference value, stop when you find it, and record the position of the pointer
  3. Then start from the head to the tail to search for an element larger than the reference value, stop the search, and record the position of the pointer
  4. Swap elements of the current left and right pointer positions
  5. Repeat steps 2, 3 and 4 until the value of the left pointer is greater than that of the right pointer

• code implementation

public class QuickSort {
    /**
     * Quick sort
     *
     * @param c
     */
    public static void sort(Comparable[] c) {
        int lo = 0;
        int hi = c.length - 1;
        sort(c, lo, hi);
    }

    /**
     * Sort the elements in array c from index lo to hi
     *
     * @param c
     * @param lo
     * @param hi
     */
    private static void sort(Comparable[] c, int lo, int hi) {
        // Parameter validity check
        if (hi <= lo) {
            return;
        }

        // Slice array c
        int partition = partition(c, lo, hi);

        // Sort the left and right sub arrays respectively
        sort(c, lo, partition - 1);
        sort(c, partition + 1, hi);
    }

    /**
     * Segment the elements from index lo to hi in array c, and return the index value of the last grouping boundary
     *
     * @param c
     * @param lo
     * @param hi
     * @return
     */
    private static int partition(Comparable[] c, int lo, int hi) {
        // Confirm critical value
        Comparable key = c[lo];

        // Define left and right pointers; Point to the smallest index and the next largest index of the index to be segmented respectively
        int left = lo;
        int right = hi + 1;

        // segmentation
        while (true) {
            // Scan from right to left, move the right pointer, find an element smaller than the critical value, and stop
            while (less(key, c[--right])) {
                if (right <= lo) {
                    break;
                }
            }

            // Scan from left to right, move the left pointer, find an element larger than the critical value, and stop
            while (less(c[++left], key)) {
                if (left >= hi) {
                    break;
                }
            }

            // Judge left > = right; If yes, the scan ends; If not, swap elements
            if (left >= right) {
                break;
            } else {
                exch(c, left, right);
            }
        }

        // Exchange boundary value
        exch(c, lo, right);

        // Return boundary value index
        return right;
    }

    /**
     * Determine whether c1 is less than c2
     *
     * @param c1
     * @param c2
     * @return
     */
    private static boolean less(Comparable c1, Comparable c2) {
        return c1.compareTo(c2) < 0;
    }

    /**
     * Swap the elements at indexes i and j in array c
     *
     * @param c
     * @param i
     * @param j
     */
    private static void exch(Comparable[] c, int i, int j) {
        Comparable temp = c[i];
        c[i] = c[j];
        c[j] = temp;
    }
}

public class SortTest {
    /**
     * Quick sort
     */
    @Test
    public void testQuickSort(){
        Integer[] c = {6, 1, 2, 7, 9, 3, 4, 5, 8};
        System.out.println("Before sorting:" + Arrays.toString(c));
        QuickSort.sort(c);
        System.out.println("After sorting:" + Arrays.toString(c));
    }
}

Before sorting:[6, 1, 2, 7, 9, 3, 4, 5, 8]
After sorting:[1, 2, 3, 4, 5, 6, 7, 8, 9]

• The difference between quick sort and merge sort

  • Quick sort is another divide and conquer sorting algorithm. It divides an array into two sub arrays and sorts the two parts independently

  • Quick sort and merge sort are complementary:

    Merge sort divides the array into two sub arrays to sort them respectively, and merges the ordered sub arrays to sort the whole array. The way of quick sort is that when both arrays are ordered, the whole array will be ordered naturally. In merge sort, an array is equally divided into two parts, and the merge call occurs before processing the entire array

    In quick sort, the position of the segmented array depends on the contents of the array, and recursive calls occur after processing the entire array

• Time complexity analysis

  The first segmentation of quick sort starts from both ends and searches alternately until left and right coincide. Therefore, the time complexity of the first segmentation algorithm is O(n), but the time complexity of the whole quick sort is related to the number of segmentation.

  Optimal situation: the benchmark number selected for each segmentation just divides the current sequence equally.

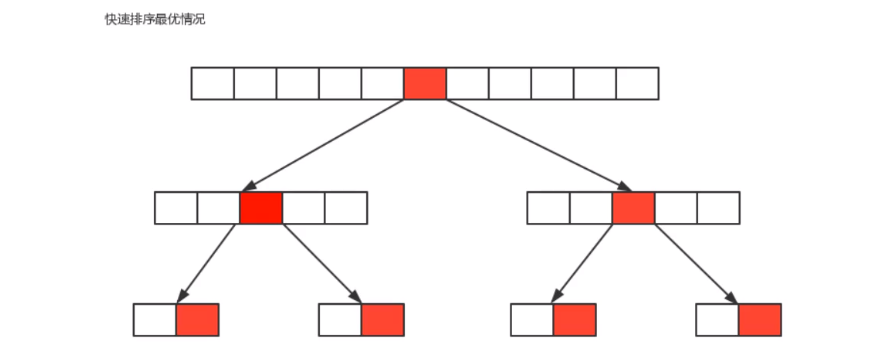
If we regard the segmentation of an array as a tree, the above figure is a diagram of its optimal situation, which has been segmented logn times

Therefore, in the optimal case, the time complexity of quick sorting is O(n*logn) logarithmic order

**Worst case: * * the benchmark number selected for each segmentation is the maximum number or the minimum number in the current sequence, which makes each segmentation have a subgroup, so the total
In the worst case, the time complexity of quick sorting is O(n^2) square order

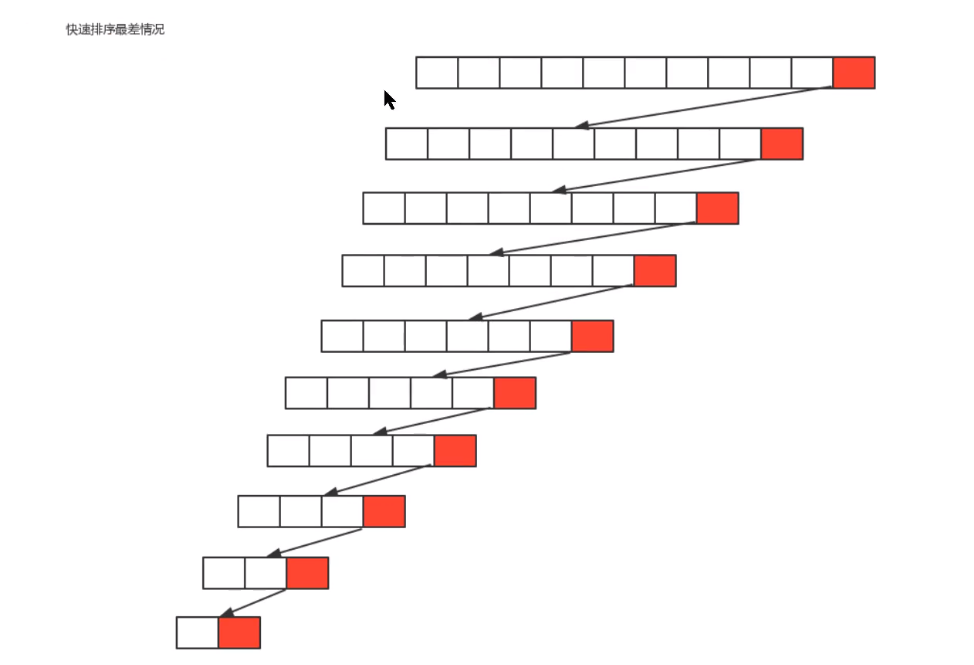
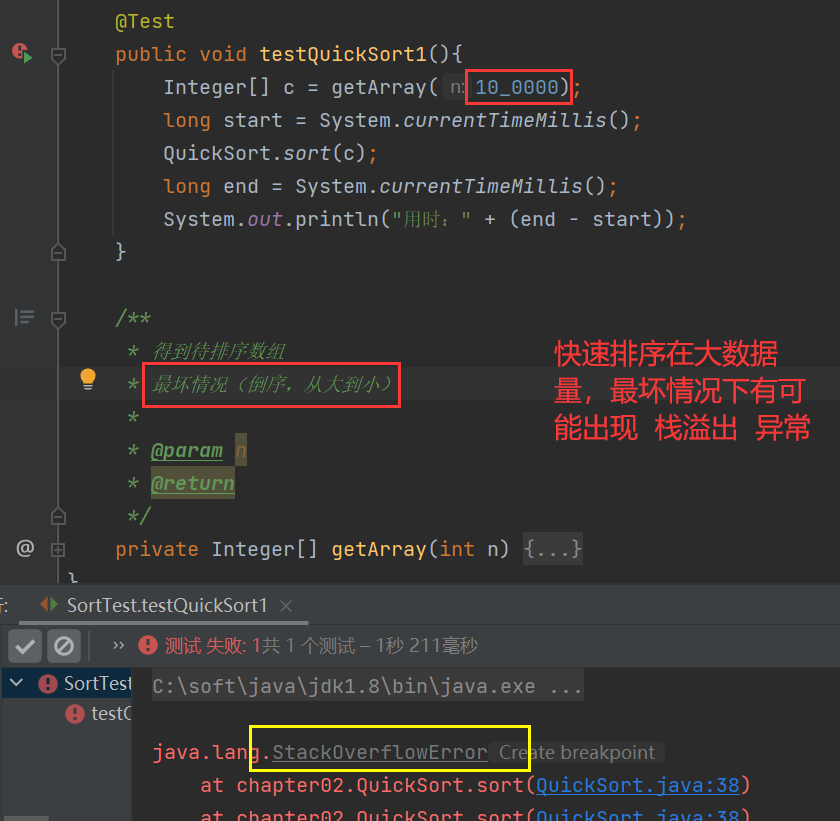
**Average case: * * the benchmark number selected for each segmentation is neither the maximum value nor the minimum value nor the median value. In this case, we can also prove by mathematical induction that the average time complexity of quick sorting is O(n*logn) (logarithmic order)

4.4 stability of sorting

• definition

  There are several elements in array arr, in which element A is equal to element B, and element A is in front of element B. If A sorting algorithm is used to sort, it can ensure that element A is still in front of element B, it can be said that the algorithm is stable

  In short: after the equal elements are sorted, the front and rear positions remain unchanged, that is, they are stable

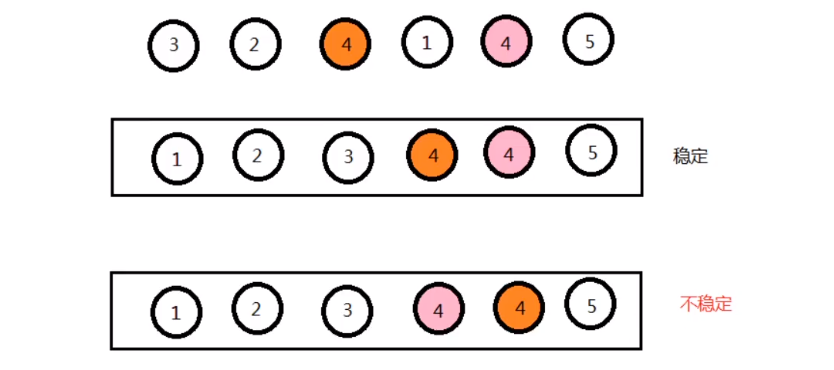
• Significance of stability

  • If a group of data only needs to be sorted once, stability is generally meaningless

  • If a set of data needs to be sorted multiple times, stability makes sense

    For example:

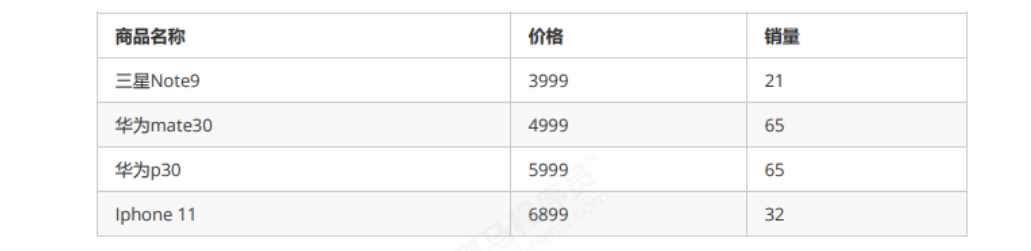
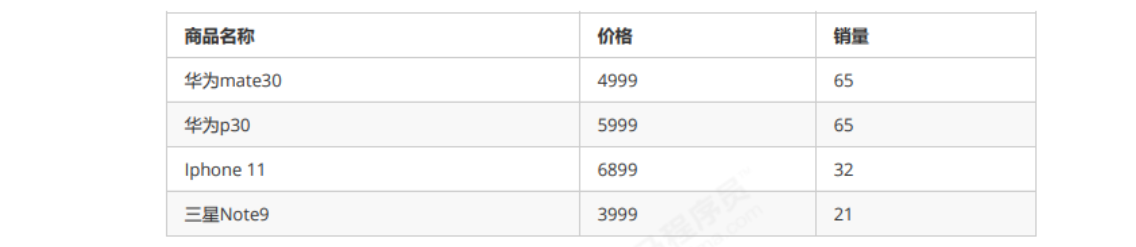
    The content to be sorted is a group of commodity objects. The first sort is sorted from low to high according to the price, and the second sort is sorted from high to low according to the sales volume. If the stability algorithm is used in the second sort, the objects with the same sales volume can still be displayed in the order of high and low prices. Only objects with different sales volumes need to be reordered. In this way, the original meaning of the first sorting can be maintained and the system overhead can be reduced

    First ranking by price from low to high:

For the second time, it is sorted from high to low according to sales volume:

• Comparison of common sorting algorithms

Sorting algorithm	stability	Time complexity	performance	recommend
Bubble sorting	stable	O(N^2) (square order)	low	Small amount of data
Select sort	instable	O(N^2) (square order)	low	Small amount of data
Insert sort	stable	O(N^2) (square order)	low	Small amount of data
Shell Sort	instable	-	high	Large amount of data; Recommended for single query
Merge sort	stable	O(n*logn) (logarithmic order)	high	Large amount of data; Recommended for multiple queries
Quick sort	instable	O(n*logn) (logarithmic order)	high	Large amount of data (possible stack overflow)

• Bubble sort: only when arr [i] > arr [i + 1], the position of elements will be exchanged, and when they are equal, the position will not be exchanged
• Select Sorting: select the smallest element for each position, such as data {5 (1), 8, 5 (2), 2, 9}. The smallest element selected for the first time is 2, so 5 (1) will exchange positions with 2. At this time, 5 (1) goes behind 5 (2), which destroys the stability
• Insertion sort: the comparison starts from the end of the ordered sequence, that is, the element to be inserted is compared with the largest element that has been ordered. If it is larger than it, it is directly inserted behind it. Otherwise, it goes straight ahead until the insertion position is found. If you encounter an element that is equal to the inserted element, put the element to be inserted after the equal element. Therefore, the sequence of equal elements has not changed. The order out of the original unordered sequence is the order after the order
• Hill sort: insert and sort elements according to the unsynchronized length. Although one insertion sort is stable and will not change the relative order of the same elements, in different insertion sorting processes, the same elements may move in their own insertion sort, and finally their stability will be disturbed
• Merge sort: in the process of merging, the position will be exchanged only when arr [i] < arr [i + 1]. If the two elements are equal, the position will not be exchanged, so it will not destroy the stability
• Quick sort: you need a benchmark value. Find an element smaller than the benchmark value on the right side of the benchmark value and an element larger than the benchmark value on the left side of the benchmark value, and then exchange the two elements. At this time, the stability will be destroyed