chart
1, Figure basic introduction
1. Why is there a map
- We learned linear tables and trees earlier
- The linear table is limited to the relationship between a direct precursor and a direct successor
- The tree can only have one direct precursor, that is, the parent node
- When we need to represent many to many relationships, we use graphs here.
2. Illustration of figure
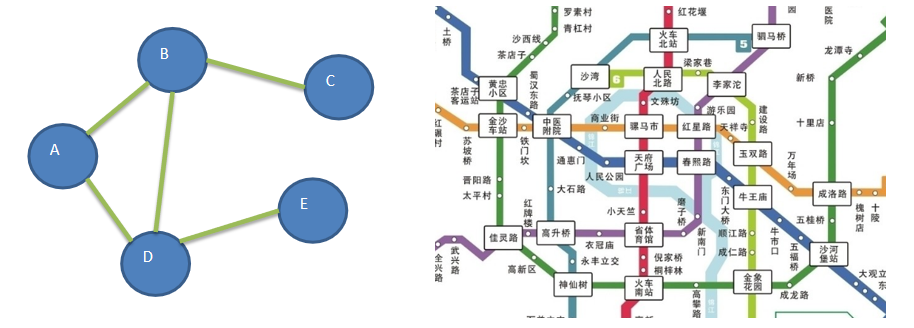
A graph is a data structure in which a node can have zero or more adjacent elements. The connection between two nodes is called an edge. Nodes can also be called vertices. As shown in the figure:
3. Common concepts of graph
- Vertex
- Edge
- route
- Undirected graph
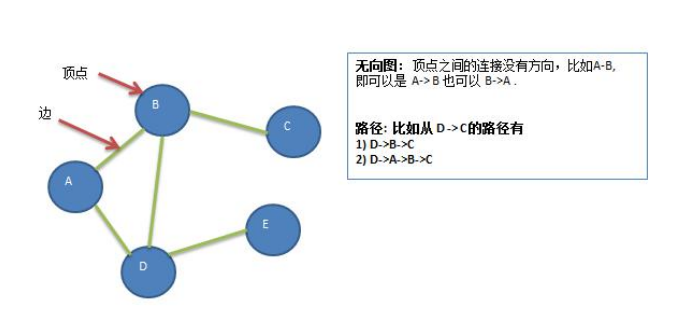
- Directed graph
- Weighted graph
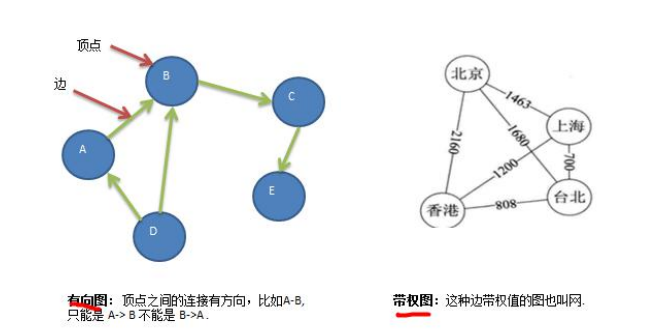
2, Representation of Graphs
There are two representations of graphs: two-dimensional array representation (adjacency matrix); Linked list representation (adjacency list).
1. Adjacency matrix
Adjacency matrix is a matrix that represents the adjacency relationship between vertices in a graph. For a graph with n vertices, row and col represent 1... N points.
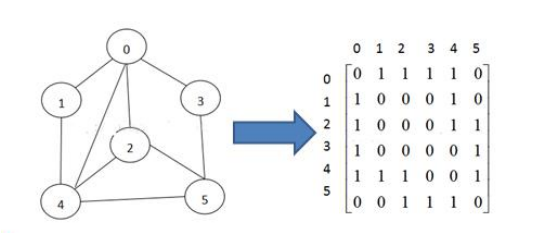
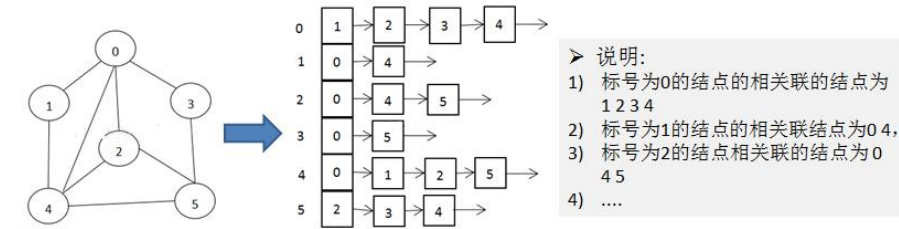
2. Adjacency table
- Adjacency matrix needs to allocate n edge spaces for each vertex. In fact, many edges do not exist, which will cause a certain loss of space
- The implementation of adjacency table only cares about the existing edges, not the nonexistent edges. Therefore, there is no space waste. The adjacency table is composed of array + linked list
- Examples
3, Figure quick start case
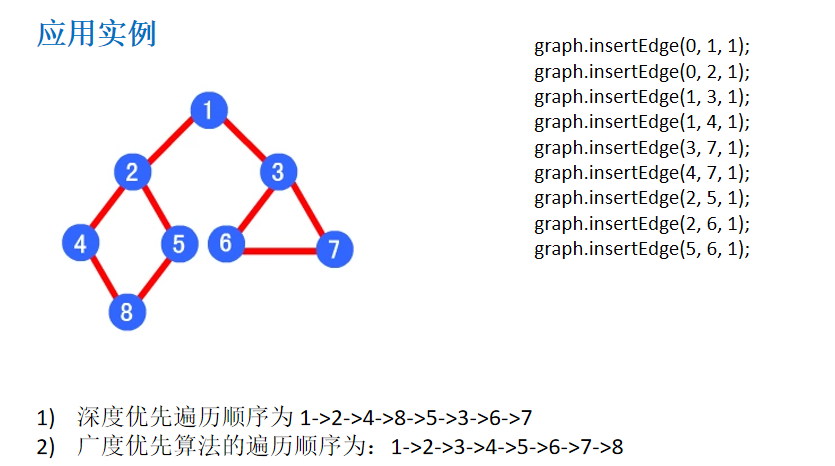
- Requirements: the code implementation is shown in the following figure

- Train of thought analysis (1) store vertex String and use ArrayList (2) to save matrix int[][] edges
- code implementation
public class Graph {
private ArrayList<String> vertexList; //Store vertex sets
private int[][] edges; //Storage graph corresponding adjacency matrix
private int numOfEdges; //Represents the number of edges
public static void main(String[] args) {
//Test whether a graph is created ok
int n = 8; //Number of nodes
String Vertexs[] = {"A", "B", "C", "D", "E"};
//Create graph object
Graph graph = new Graph(n);
//Adding vertices to a loop
for(String vertex: Vertexs) {
graph.insertVertex(vertex);
}
//Add edge
//A-B A-C B-C B-D B-E
graph.insertEdge(0, 1, 1); // A-B
graph.insertEdge(0, 2, 1); //
graph.insertEdge(1, 2, 1); //
graph.insertEdge(1, 3, 1); //
graph.insertEdge(1, 4, 1); //
//Display an adjacency matrix
graph.showGraph();
}
//constructor
public Graph(int n) {
//Initialize matrix and vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
//Common methods in Figure
//Returns the number of nodes
public int getNumOfVertex() {
return vertexList.size();
}
//Display the matrix corresponding to the figure
public void showGraph() {
for(int[] link : edges) {
System.err.println(Arrays.toString(link));
}
}
//Get the number of edges
public int getNumOfEdges() {
return numOfEdges;
}
//Return the data corresponding to node i (subscript) 0 - > "a" 1 - > "B" 2 - > "C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//Returns the weights of v1 and v2
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//Insert Knot
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//Add edge
/**
*
* @param v1 Indicates the subscript of the point, even if the first vertex is "a" - "B", "a" - > 0 "B" - > 1
* @param v2 Subscript corresponding to the second vertex
* @param weight express
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}
4, Figure introduction to traversal
The so-called graph traversal is the access to nodes. There are so many nodes in a graph. How to traverse these nodes requires specific strategies. Generally, there are two access strategies: (1) depth first traversal (2) breadth first traversal
1. The depth of the graph is traversed first
1.1 basic idea
Depth first search of graph.
- Depth first traversal: starting from the initial access node, the initial access node may have multiple adjacent nodes. The strategy of depth first traversal is to first access the first adjacent node, and then use the accessed adjacent node as the initial node to access its first adjacent node, It can be understood as follows: after accessing the current node every time, first access the first adjacent node of the current node.
- We can see that such an access strategy gives priority to vertical mining, rather than horizontal access to all adjacent nodes of a node.
- Obviously, depth first search is a recursive process
1.2 depth first traversal algorithm steps
- Access the initial node v and mark node v as accessed.
- Find the first adjacent node w of node v.
- If w exists, continue with 4. If w does not exist, return to step 1 and continue from the next node of v.
- If W is not accessed, perform depth first traversal recursion on w (that is, treat w as another v, and then proceed to step 123).
- If W is accessed, find the next adjacent node of the w adjacent node of node v, and go to step 3.
1.3 code implementation
//Depth first traversal algorithm
//i is 0 for the first time
private void dfs(boolean[] isVisited, int i) {
//First, we access the node and output
System.out.print(getValueByIndex(i) + "->");
//Set the node as accessed
isVisited[i] = true;
//Find the first adjacent node w of node i
int w = getFirstNeighbor(i);
while(w != -1) {//Description yes
if(!isVisited[w]) {
dfs(isVisited, w);
}
//If the w node has been accessed
w = getNextNeighbor(i, w);
}
}
//Carry out an overload on dfs, traverse all our nodes, and carry out dfs
public void dfs() {
isVisited = new boolean[vertexList.size()];
//Traverse all nodes and perform dfs [backtracking]
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
dfs(isVisited, i);
}
}
}
2. Breadth first traversal of Graphs
2.1 basic idea of breadth first traversal
- Broad first search of graph.
- Similar to a hierarchical search process, breadth first traversal needs to use a queue to maintain the order of visited nodes, so as to access the adjacent nodes of these nodes in this order
2.2 breadth first traversal algorithm steps
-
Access the initial node v and mark node v as accessed.
-
Node v in queue
-
When the queue is not empty, continue to execute, otherwise the algorithm ends.
-
Out of the queue, get the queue head node u.
-
Find the first adjacent node w of node u.
-
If the adjacent node w of node u does not exist, go to step 3; Otherwise, the loop performs the following three steps:
6.1 if node w has not been accessed, access node W and mark it as accessed.
6.2 node w in queue
6.3 find the next adjacent node w of node u after the adjacent node W, and go to step 6.
2.3 code implementation
//A method of breadth first traversal of a node
private void bfs(boolean[] isVisited, int i) {
int u ; // Indicates the subscript corresponding to the head node of the queue
int w ; // Adjacent node w
//Queue, which records the access order of nodes
LinkedList queue = new LinkedList();
//Access node and output node information
System.out.print(getValueByIndex(i) + "=>");
//Mark as accessed
isVisited[i] = true;
//Add node to queue
queue.addLast(i);
while( !queue.isEmpty()) {
//Take out the subscript of the header node of the queue
u = (Integer)queue.removeFirst();
//Get the subscript w of the first adjacent node
w = getFirstNeighbor(u);
while(w != -1) {//find
//Have you visited
if(!isVisited[w]) {
System.out.print(getValueByIndex(w) + "=>");
//Mark already accessed
isVisited[w] = true;
//Join the team
queue.addLast(w);
}
//Take u as the precursor point and find the next neighbor node after w
w = getNextNeighbor(u, w); //Reflect our breadth first
}
}
}
//Traverse all nodes and perform breadth first search
public void bfs() {
isVisited = new boolean[vertexList.size()];
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
bfs(isVisited, i);
}
}
}
5, Code summary of figure
public class Graph {
private ArrayList<String> vertexList; //Store vertex sets
private int[][] edges; //Storage graph corresponding adjacency matrix
private int numOfEdges; //Represents the number of edges
//Define the boolean [] array to record whether a node is accessed
private boolean[] isVisited;
public static void main(String[] args) {
//Test whether a graph is created ok
int n = 8; //Number of nodes
//String Vertexs[] = {"A", "B", "C", "D", "E"};
String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
//Create graph object
Graph graph = new Graph(n);
//Adding vertices to a loop
for(String vertex: Vertexs) {
graph.insertVertex(vertex);
}
//Add edge
//A-B A-C B-C B-D B-E
// graph.insertEdge(0, 1, 1); // A-B
// graph.insertEdge(0, 2, 1); //
// graph.insertEdge(1, 2, 1); //
// graph.insertEdge(1, 3, 1); //
// graph.insertEdge(1, 4, 1); //
//Update edge relationships
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 1);
graph.insertEdge(5, 6, 1);
//Display an adjacency matrix
graph.showGraph();
//Test whether our dfs traversal is ok
System.out.println("depth-first traversal ");
graph.dfs(); // A->B->C->D->E [1->2->4->8->5->3->6->7]
// System.out.println();
System.out.println("Breadth first!");
graph.bfs(); // A->B->C->D-E [1->2->3->4->5->6->7->8]
}
//constructor
public Graph(int n) {
//Initialize matrix and vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
//Get the subscript w of the first adjacent node
/**
*
* @param index
* @return If it exists, it returns the corresponding subscript; otherwise, it returns - 1
*/
public int getFirstNeighbor(int index) {
for(int j = 0; j < vertexList.size(); j++) {
if(edges[index][j] > 0) {
return j;
}
}
return -1;
}
//The next adjacent node is obtained according to the subscript of the previous adjacent node
public int getNextNeighbor(int v1, int v2) {
for(int j = v2 + 1; j < vertexList.size(); j++) {
if(edges[v1][j] > 0) {
return j;
}
}
return -1;
}
//Depth first traversal algorithm
//i is 0 for the first time
private void dfs(boolean[] isVisited, int i) {
//First, we access the node and output
System.out.print(getValueByIndex(i) + "->");
//Set the node as accessed
isVisited[i] = true;
//Find the first adjacent node w of node i
int w = getFirstNeighbor(i);
while(w != -1) {//Description yes
if(!isVisited[w]) {
dfs(isVisited, w);
}
//If the w node has been accessed
w = getNextNeighbor(i, w);
}
}
//Carry out an overload on dfs, traverse all our nodes, and perform dfs
public void dfs() {
isVisited = new boolean[vertexList.size()];
//Traverse all nodes and perform dfs [backtracking]
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
dfs(isVisited, i);
}
}
}
//A method of breadth first traversal of a node
private void bfs(boolean[] isVisited, int i) {
int u ; // Indicates the subscript corresponding to the head node of the queue
int w ; // Adjacent node w
//Queue, which records the access order of nodes
LinkedList queue = new LinkedList();
//Access node and output node information
System.out.print(getValueByIndex(i) + "=>");
//Mark as accessed
isVisited[i] = true;
//Add node to queue
queue.addLast(i);
while( !queue.isEmpty()) {
//Fetch the subscript of the header node of the queue
u = (Integer)queue.removeFirst();
//Get the subscript w of the first adjacent node
w = getFirstNeighbor(u);
while(w != -1) {//find
//Have you visited
if(!isVisited[w]) {
System.out.print(getValueByIndex(w) + "=>");
//Mark already accessed
isVisited[w] = true;
//Join the team
queue.addLast(w);
}
//Take u as the precursor point and find the next neighbor node after w
w = getNextNeighbor(u, w); //Reflect our breadth first
}
}
}
//Traverse all nodes and perform breadth first search
public void bfs() {
isVisited = new boolean[vertexList.size()];
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
bfs(isVisited, i);
}
}
}
//Common methods in Figure
//Returns the number of nodes
public int getNumOfVertex() {
return vertexList.size();
}
//Display the matrix corresponding to the figure
public void showGraph() {
for(int[] link : edges) {
System.err.println(Arrays.toString(link));
}
}
//Get the number of edges
public int getNumOfEdges() {
return numOfEdges;
}
//Return the data corresponding to node i (subscript) 0 - > "a" 1 - > "B" 2 - > "C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//Returns the weights of v1 and v2
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//Insert Knot
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//Add edge
/**
*
* @param v1 Indicates the subscript of the point, even if the first vertex is "a" - "B", "a" - > 0 "B" - > 1
* @param v2 Subscript corresponding to the second vertex
* @param weight express
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}
6, Depth first VS breadth first