Hashtable

• Hash table -- hash table
  • Hash table is a very important data structure. Almost all programming languages use or indirectly use hash table
  • Its structure is an array, but its difference from the array is the transformation of the subscript value, which is called the hash function, and the HashCode is obtained through the hash function
    
    
• Hash table is usually implemented based on array, but it has many advantages over array
  • It allows very fast insert delete find operations
  • No matter how much data, the insertion and deletion of values need to be close to a constant time: that is, the time level of O (1). In fact, it only needs a few machine instructions to complete
  • The speed of hash table is faster than that of tree. It can basically find the desired elements in an instant
  • Hash table coding is much easier than tree coding
    
    
• Hash tables have some disadvantages over arrays
  • The data in the hash table is out of order, so the elements in the hash table cannot be traversed in a conventional way
  • Generally, the key value in the hash table is not allowed to be null, and the same key cannot be placed to save different elements

structure

When we store a value (number, character, bool, etc.) into the hash table, the hash function encodes the data into a large integer, compresses the large integer, obtains the subscript value of the data in the array structure through hashing, and then directly stores the value in the corresponding array position, and then queries and modifies it, For deletion, only the subscript obtained by hashing the query value directly goes to the corresponding subscript position to get the data. There is no need to traverse, and the efficiency will be much higher.

hash function

Convert words or other data into large numbers. The code implementation of hashing large numbers is put in a function, which is called hash function

Character to integer

• Word / string to subscript value is actually letter / text to number

  • Now we need to design a scheme that can turn words into appropriate subscripts
    • In fact, there are many coding schemes in the computer, that is, to replace the characters of words with numbers
    • Such as character encoding·
    • ASCII coding, but also to their own design coding
    • We can use Utf - 8 coding

• How to turn?

• Digital addition scheme

  • Use the position of words in the word list

  • For example, cats = 3 + 1 + 20 + 17 = 41; When querying the hash table, you only need to query the subscript 41 to find the word cats

  • Disadvantages: not complex enough and easy to repeat

• Power multiplication scheme

  • It can basically meet the uniqueness of numbers and will not be repeated with other words

  • E.g. 7654 = 710 ³ + six hundred and ten ² + 5*10 + 4；

  • Then the word can also be expressed as cats = 327 ³ + one hundred and twenty-seven ² + 20*27 + 17 = 60337

  • At this time, 60337 is the subscript of the word cats in the hash table. When querying the hash table, you only need to query the subscript 60337 to find the word cats

  • shortcoming

  • Creating meaningless words, such as yyyyyyyy, wastes space, and the array cannot represent such a large subscript value

When we get a large value, the general size will be very large. If we create an array of corresponding length, it will be a waste of space. At this time, we need to carry out certain compression operations to control the data within an acceptable range.

Hashing

• Hashing
  • Now we need a compression method to compress the huge integer range obtained by concatenation to an acceptable range, so as to avoid that the array cannot represent such a large subscript range
  • Generally, a lot of space is required to store data, because it is not guaranteed that each data can be fully mapped to each position of the array (some positions do not necessarily have only one data)
    
    
  • compress
    • Now compress the excessive power multiplication data to an acceptable range
    • Operation: residual
      • Gets the remainder of a number divided by another number
      • Suppose we want to compress the maximum value of 10000 to the maximum value of 100
      • We first set a hash table subscript value index = 10000 / 100 = 100;
      • When there is a data 23459, it will be stored in the hash table in the range of (23459% index) = 9, and the value of 120 will be stored in (120% index = 0)
        This range is in the hash table.
      • There will also be duplication
        
        
  • concept
    • Hashing: the process of converting large numbers into subscripts within the array range is called hashing.
    • Hash function: convert words or other data into large numbers. The code implementation of hashing large numbers is put in a function. This function is called hash function, such as the previous one (10000% 100)
    • Hash table: finally, the data is inserted into this array to encapsulate the whole structure, which is called hash table

After the data is converted into large numbers by power multiplication, it is impossible to directly open the space of the corresponding size on the array (waste space, some space is not used). At this time, the number obtained after hashing can be used as a subscript and put the value into the array of the corresponding subscript. For example, there is an array with a length of 8 (the size of the corresponding hashed remainder is 9), The number 23344 corresponds to the position of subscript 4, and the number 125 corresponds to the position of subscript 5····

Hash Collisions

We found that the index values obtained by hashing the stored values may be repeated (although this possibility is not high), but once a hash conflict occurs, the previous data will be overwritten by the subsequent data. In this case, it is necessary to solve the hash conflict

When multiple data appear at the same subscript position, data may be inserted at this time, which may lead to previous data loss
The common solutions are chain address method and open address method

Chain address method

• By using a linked list or array to store data at the subscript position, multiple data can be stored at one subscript position. When querying, you can query according to the query method of linked list or array

• When a linked list is used, data is usually inserted from the head or tail. If an array is used, it is usually inserted from the tail for performance priority

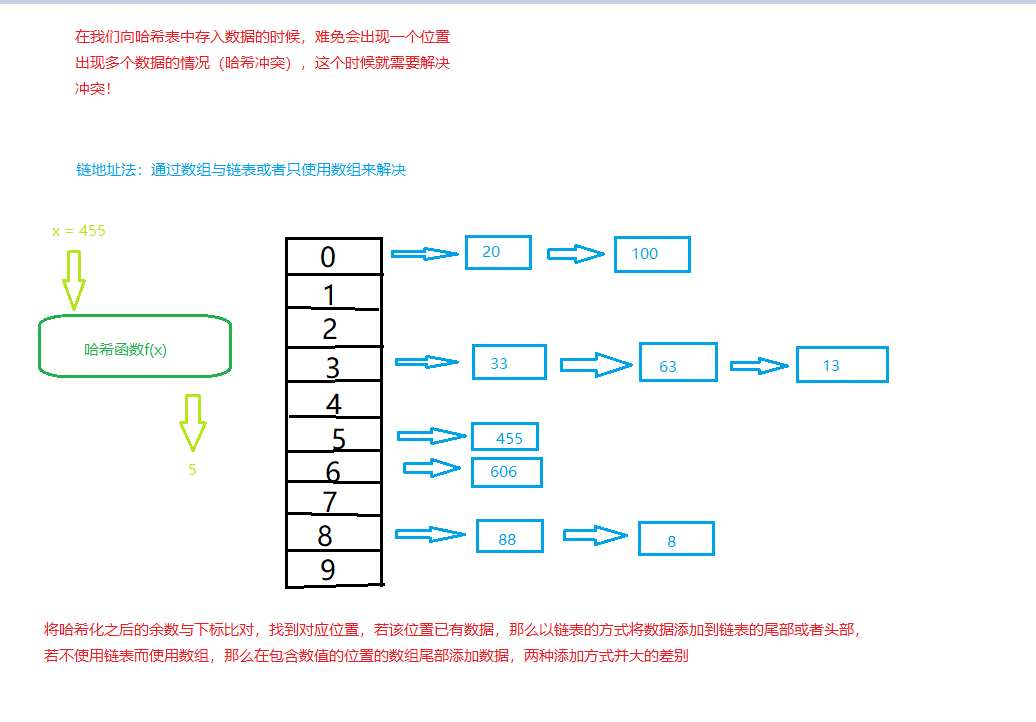
When there is a conflict. The inserted data will be filled into the array or linked list to avoid data loss.

Open address method

It is mainly to find a blank location to add data, but there are three methods to find this location

Linear detection

• When there is data in the current location, the location will be searched from the next location. When an empty location is found, the data will be inserted

• When searching this data, first query whether the current location data is the same as the query data. If it is the same, this value will be returned. If it is different, continue to search the query value from the next location. When a blank location is encountered, terminate the query. (because the value (duplicate) will only be placed in the first blank position. If a null value is found and the value is still not found, it is impossible to have the value later. Terminate the query to avoid affecting performance).

• When a value is deleted, the current position should specify a special value (such as - 1). When the query data encounters this value (- 1), continue to query backward to avoid affecting the query of subsequent data due to the null value after deleting the data in the specified position (interrupting the query).
  

Secondary detection
Problems with linear queries,

• When there is no data, when we insert a piece of data gathered in a certain position, it will affect the performance of hash table query. When we query a piece of data, and its original position is occupied by other elements, and there are many other continuous data in its lower position, if we want to query it, we must query the data in this area again and again, Until the element inserted in other areas is queried

gather

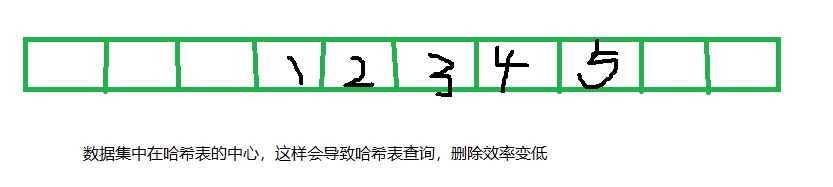
• Secondary detection to solve the aggregation problem
  Secondary detection is mainly to solve the problem of step size of linear detection. Ordinary linear detection can be regarded as detection with step size of 1, and secondary detection can be regarded as detection across multiple columns, such as span (x is the subscript value) x+1, x+2 ²··· (if the following scale value is 2, then the steps are (3,6,10)) this can detect a long distance at one time and avoid the impact of aggregation

double hashing
Problems in secondary detection when we insert the value of the same subscript (1210211222 ·); At this time, if the step size of the secondary detection is the same, there will also be a performance problem. This problem can be solved by hashing it again

Efficiency of hashing

Efficiency of hashing

- If there is no conflict, the efficiency will be higher

- If a conflict occurs, the access time depends on the subsequent probe length(That is, the amount of data in the linked list or array corresponding to each subscript of the array). 

- Average probe length and average access time, depending on`Load Factor `，As the loading factor increases, the length of detection becomes longer and longer.

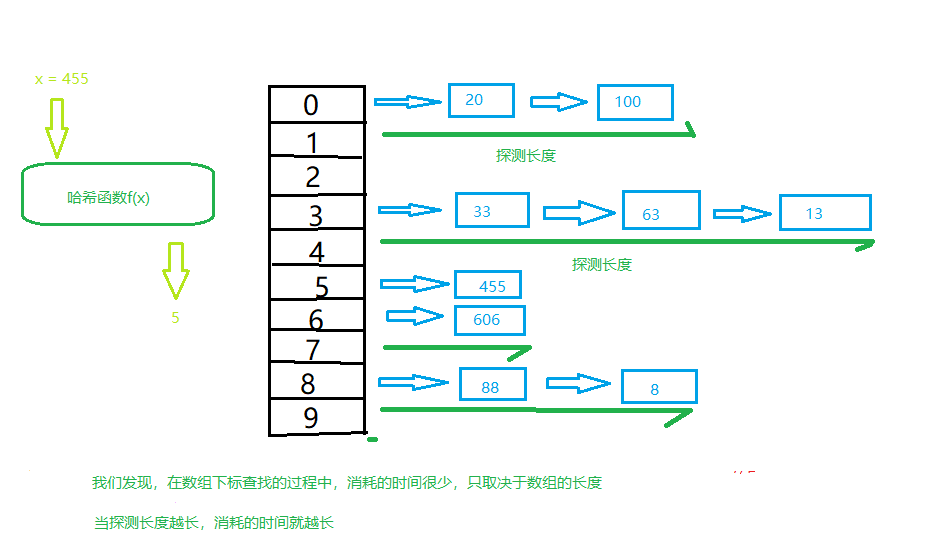
• Load Factor
  • The loading factor represents the ratio of the data items already contained in the current hash table to the length of the entire hash table.
  • Loading factor = total data item / hash table length
  • The loading factor of open address method is up to 1, because it must find a blank cell to put elements into
  • The filling factor of the chain address method can be greater than 1, because the zipper method can extend indefinitely

In theory, the open address method is much more efficient.
Generally, when the data item has occupied half of the length of the hash table, the hash expansion should be considered.

Horner's rule in hashing (Qin Jiushao algorithm)

Apply to hash function
- Pn(x) = anx^n + a(n-1)x^(n-1)+···+ a1x + a0 = ((···(((anx + an - 1)x + an - 2)x + an -3)···)x+a1)x + a0

Implement hash table (chain address method to solve hash conflict [use array])

Encapsulate a hash function

// Encapsulate a hash function
// -Converts a string to a larger number hashCode
// -Compress larger numbers into the range of the array (hash table length)
// -Returns the location of the stored subscript value
function hashFunc(str, size): number {
   // Define hashcode variables
   let hashCode: number = null;

   // The hashcode value is calculated by Qin Jiushao algorithm
   // Convert str to unicode encoding
   for (let i = 0; i < str.length; i++) {
       hashCode = 37 * hashCode + str.charCodeAt(i);
   }

   // Surplus
   let index: number = hashCode % size;
  //Return subscript position
   return index;
}

Where str is the stored data - which will be converted to large numbers
size is the length of the designed hash table (the remainder of large numbers is used to compress large numbers)
index returns the subscript position in the array

Encapsulate hash table

// Encapsulate hash table
class MyHashTable {
    // Hashtable 
    private message: unknown[] = [];
    // The number of elements already stored in the hash table
    private count: number = 0;
    // Length of hash table (length of compressed array)
    private limit: number = 10;

    // hash function 
    private runHashFunc(str: unknown, size: number): number {
        return hashFunc(str, size);
    }

    // Hash table insertion and modification methods
    alter(key: unknown, value: number): boolean {
        let index: number;

        // Get the corresponding index (subscript position) according to the key (hashed)
        index = this.runHashFunc(key, this.limit);

        // Gets the array corresponding to the subscript position
        let bunck: unknown = this.message[index];

        // When there is no array at the corresponding subscript position, create an array and place it at the corresponding subscript position
        if (bunck === undefined) {
            bunck = [];
            this.message[index] = bunck;
        }

        // In case of modification
        for (let i = 0; i < bunck.length; i++) {
            // Find the key of the qualified array group corresponding to the subscript and modify the key
            if (bunck[i][0] === key) {
                bunck[i][1] = key;
                return true;
            }
        }

        //Insert operation
        bunck.push([key, value]);
        this.count += 1;
        return true;
    }

    // Acquisition method
    getNode(key: unknown): unknown {
        // To get the index, you need to use the hash function
        let index: number = this.runHashFunc(key, this.limit);

        // Find the array corresponding to the subscript
        let bunck: unknown[] = this.message[index];

        // Judge whether there is stored data in this subscript
        if (bunck === undefined) {
            return false;
        }

        // Traverse the array of corresponding Subscripts
        for (let i: number = 0; i < bunck.length; i++) {
            if (bunck[i][0] === key) {
                // If yes, the corresponding value is returned
                return bunck[i][1];
            }
        }
        return false;
    }

    // Delete method
    remove(key: unknown): boolean {
        // To get the index, you need to use the hash function
        let index: number;
        index = this.runHashFunc(key, this.limit);

        // Find the array corresponding to the subscript
        let bunck: unknown[] = this.message[index];

        // Judge whether there is stored data in this subscript
        if (bunck === undefined) {
            return false;
        }

        // Traverse the array of corresponding Subscripts
        for (let i: number = 0; i < bunck.length; i++) {
            if (bunck[i][0] === key) {
                // If found, the element (array) corresponding to the subscript array is returned
                bunck.splice(i, 1);
                // Hash table length containing data - 1
                this.count -= 1;
                return true;
            }
        }
        return false
    }

    //Judge whether the hash table is empty
    isEmpty():boolean{
        return this.count === 0;
    }

    //Gets the number of hash table elements
    size():number{
        return this.count;
    }
}

Note that value is the description and data of the corresponding key data

test

let hash = new MyHashTable();
hash.alter('a', 4);
hash.alter('b', 33);
hash.alter('s', 45);
hash.alter('ae', 4);
hash.alter('bg', 333);
hash.alter('rs', 444);
console.log(hash.getNode('s'));
//45
console.log(hash.getNode('a'));
//4

hash.remove('a');
console.log(hash.getNode('a'));
//false

Expansion of hash table

• Theoretically, the data stored in the subscript position of the hash table can be extended infinitely, but with the increase of the amount of data, the detection length will become larger and larger, and the detection here mainly uses ordinary traversal, resulting in lower and lower efficiency. We need to expand the capacity at the appropriate position

• It is best to expand the hash table. The final capacity is prime, and all data must be reinserted after expansion (because the subscript position obtained after hashing has changed)

• The time for capacity expansion is generally when hashcode (fill factor) > 0.75

Implementation of capacity expansion

import {myHash} from "./Implement hash table";

// Implementation of capacity expansion
class ResizeHashTable extends myHash {

    // Hash table insertion and modification methods
    alter(key: unknown, value: number): boolean {
        let index: number;

        // Get the corresponding index (subscript) according to the key (hashed)
        index = this.runHashFunc(key, this.limit);

        // When number of data items / hash table length = fill factor > 0.75
        if (this.count / this.limit >= 0.75) {
            console.warn('The hash table data capacity is about to overflow. Please expand it in time hash');
            // Automatic capacity expansion twice the current hash length
            let newSize: number = this.limit * 2,
                // Gets a prime number of suitable length
                newPirme: number = this.getPrime(newSize);
            // Capacity expansion
            this.resize(newPirme);
        }

        // Create an array with a length corresponding to the subscript position
        let bunck: unknown = this.message[index];

        // When there is no array at the corresponding subscript position, create an array and place it at the corresponding subscript position
        if (bunck === undefined) {
            bunck = [];
            this.message[index] = bunck;
        }

        // In case of modification
        for (let i = 0; i < bunck.length; i++) {
            // Find the key of the qualified tuple corresponding to the subscript and modify the key
            if (bunck[i][0] === key) {
                bunck[i][1] = key;
                return true;
            }
        }

        //Insert operation
        bunck.push([key, value]);
        this.count += 1;
        return true;
    }
-------------------------------------------------------------------
    //Override delete method
    remove(key: unknown): boolean {
        // To get the index, you need to use the hash function
        let index: number;
        index = this.runHashFunc(key, this.limit);

        // Find the array corresponding to the subscript
        let bunck: unknown[] = this.message[index];

        // Judge whether there is stored data in this subscript
        if (bunck === undefined) {
            return false;
        }

        // Traverse the array of corresponding Subscripts
        for (let i: number = 0; i < bunck.length; i++) {
            if (bunck[i][0] === key) {
                // If found, the element (array) corresponding to the subscript array is returned
                bunck.splice(i, 1);
                // Hash table length containing data - 1
                this.count -= 1;

                // When the number of data items / hash table length = fill factor < 0.25 and the minimum hash length cannot be less than 10
                if (this.count / this.limit < 0.25 && this.limit > 10) {
                    // Automatically reduce the capacity by twice the current hash length
                    let newSize: number = Math.floor(this.limit / 2),
                        // Gets a prime number of suitable length
                        newPirme: number = this.getPrime(newSize);
                    // Reduce capacity
                    this.resize(newPirme);
                }
                return true;
            }
        }
        return false
    }

------------------------------------------------------------
    // Adding a method of expanding hash table
    // Newlimit -- > new hash table length
    resize(newLimit): boolean {
        // Create a variable to receive the old hash table
        let oldHash: unknown[];
        oldHash = this.message;

        // Initializes the current hash table
        this.message = [];
        this.count = 0;
        // Change the current hash table length to the new hash table length
        this.limit = newLimit;

        // Traverse the data array corresponding to each subscript
        for (let i: number = 0; i < oldHash.length; i++) {
            // Reinsert the new hash table when there is data in the array
            if (oldHash[i] !== undefined) {
                for (let j: number = 0; j < oldHash[i].length; j++) {
                    // Add the currently traversed key and value into the new hash table
                    this.alter(oldHash[i][j][0], oldHash[i][j][1]);
                }
            } else {
                // Skip when there is no data in the current array
                continue;
            }
        }
        return true;
    }
----------------------------------------------------------------------------------
    // Get the overall hash structure
    get hash(): unknown[] {
        return this.message;
    }
--------------------------------------------------------------------------------
    // Judge prime number - used to judge whether the hash length of the expansion is a prime number so that the data is evenly distributed
    private ifnum(num: number): boolean {
        // Get square root
        let sqrt: number = Math.floor(Math.sqrt(num));
        // When it is half checked, there is no need to continue to traverse the judgment index, just like 3 * 2 = 2 * 2
        for (let i: number = 2; i < sqrt; i++) {
            if (num % i === 0) {
                return false
            }
        }
        return true;
    }
--------------------------------------------------------------------------------------------------
    // Get prime
    private getPrime(num: number): number {
        // Receive new length
        // If the new length is not a prime number, it will be incremented
        while (!this.ifnum(num)) {
            num++;
        }
        // If it is a prime number, it returns a prime number
        return num;
    }
}

let hash = new ResizeHashTable();
hash.alter('a', 4);
hash.alter('b', 33);
hash.alter('s', 45);
hash.alter('ea', 4565);
hash.alter('ae', 4);
hash.alter('bg', 333);
hash.alter('rs', 444);

// Capacity expansion
hash.resize(20);


console.log(hash.hash);
//[
//   <9 empty items>,
//   [ [ 'bg', 333 ] ],
//   [ [ 'ae', 4 ] ],
//   <2 empty items>,
//   [ [ 'rs', 444 ] ],
//   [ [ 'ea', 4565 ] ],
//   [ [ 's', 45 ] ],
//   <1 empty item>,
//   [ [ 'a', 4 ] ],
//   [ [ 'b', 33 ] ]
// ]