Linear table
Definition of linear table:
- A finite sequence consisting of n(n ≥ 0) data elements (a1,a2,..., an).
- Record as: L=(a1,a2,..., an)
ai-1 is the direct precursor of ai, and ai+1 is the direct successor of ai
a1 - first element - it has no precursor
an -- tail element - it has no successor - Table length: the number of elements in a linear table
- Empty table: a linear table without elements
Basic operation of linear table:
1.InitList(&L) //Construct empty table L. 2.LengthList(L) //Find the length of table L 3.GetElem(L,i,&e) //Take the element ai and return ai from e 4.PriorElem(L,ce,&pre_e) //Find the precursor of ce by pre_e return 5.InsertElem(&L,i,e) //Insert new element e before element ai 6.DeleteElem(&L,i) //Delete the i th element 7.EmptyList(L) //Judge whether L is an empty table
Selection and algorithm of linear table:
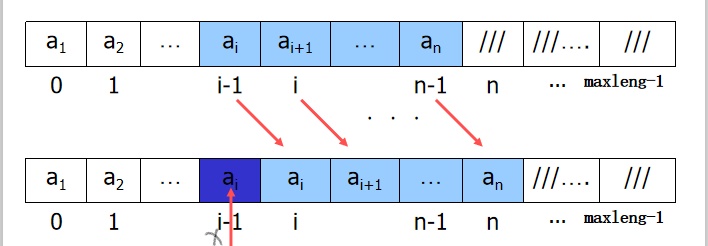
- Example 1: insert sequence table
Let there be length elements in L.elem[0... maxleng-1], insert a new element e before L.elem[i-1], (1 < = I < = length + 1)
- Algorithm 1: point to the operated linear table with a pointer and allocate it statically
#define maxleng 100
typedef struct
{ ElemType elem[maxleng];//Subscript: 0,1, maxleng-1
int length; //Table length
} SqList;
SqList L;
int Insert1(SqList *L,int i,ElemType e)
{ if (i<1||i>L->length+1) return ERROR //Illegal i value
if (L->length>=maxleng) return OVERFLOW //overflow
for (j=L->length-1;j>=i-1;j--;) //Move the following elements first (until the i-1 element is moved)
L->elem[j+1]=L->elem[j]; //Move element backward
L->elem[i-1]=e; //Insert new element
L->length++; //Length variable increases by 1
return OK; //Insert successful
}
The process is shown in the figure:
- Algorithm 2: use reference parameters to represent the operated linear table and static allocation
//L is defined as above
Status Insert2(SqList &L,int i,ElemType e) //L here is no longer a pointer
{ if (i<1||i>L.length+1) return ERROR //Illegal i value
if (L.length>=maxleng) return OVERFLOW //overflow
for (j=L.length-1;j>=i-1;j--;)
L.elem[j+1]=L.elem[j]; //Move element backward
L.elem[i-1]=e; //Insert new element
L.length++; //Length variable increases by 1
return OK //Insert successful
} //Summary: and change "* l" and "- >" to "& L" and "."
- Algorithm 3: use reference parameters to represent the operated linear table and allocate dynamically
#define LIST_INIT_SIZE 100 / / initial length
#10 / / increment
typedef struct
{ ElemType *elem;//Storage space base address
int length; //Table length
int listsize; //Currently allocated storage capacity
//(in sizeof(ElemType)
} SqList;
SqList L;
int Insert3(SqList &L,int i, ElemType e)
{int j;
if (i<1 || i>L.length+1) //The legal value of i is 1 to n+1
return ERROR;
if (L.length>=L.listsize) /*Expand on overflow*/
{
ElemType *newbase;
newbase=(ElemType *) realloc(L.elem,
(L.listsize+LISTINCREMENT)*sizeof(ElemType));
if (newbase==NULL) return OVERFLOW; //System space is full, expansion failed
L.elem=newbase; //Update linear table
L.listsize+=LISTINCREMENT; //Update current length
}
//Move the element backward to empty the component elem[i-1] of the ith element
for(j=L.length-1;j>=i-1;j--)
L.elem[j+1]=L.elem[j];
L.elem[i-1]=e; /*New element insertion*/
L.length++; /*Linear meter length plus 1*/
return OK; //Same as static allocation
}
- realloc function
- Usage: pointer name = (data type *) realloc (pointer name to change memory size, new size). Where - the new size can be large or small (if the new size is larger than the original memory size, the newly allocated part will not be initialized; if the new size is smaller than the original memory size, data loss may occur)
- Header file: #include < stdlib h> Some compilers require #include < malloc h> , at TC2 Alloc. Can be used in 0 H header file
- Return value: if the reallocation is successful, the pointer to the allocated memory is returned; otherwise, the NULL pointer is returned.
- Note: free is required when not in use
Evaluation of sequential structure:
- advantage:
(1) Is a random access structure. The time of accessing any element is a
Constant, fast speed;
(2) The structure is simple, and logically adjacent elements are also physically adjacent;
(3) Do not use pointers to save storage space. - Disadvantages:
(1) Inserting and deleting elements requires moving a large number of elements, which consumes a lot of time;
(2) A continuous storage space is required;
(3) "Overflow" may occur when inserting elements;
(4) The storage space in the free area cannot be occupied (shared) by other data.
Chain storage structure of linear list
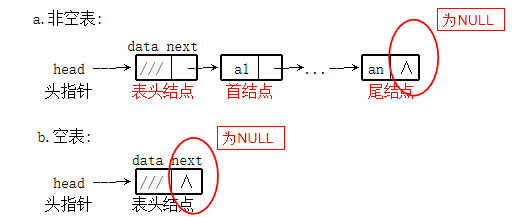
1. Single linked list:
- 1) Single linked list without header node:

- Single linked list with header node: (default type)
Definition of single linked list:
struct node //typedef can also be used
{ ElemType data; //data is an abstract element type
struct node *next; //next is the pointer type
};
Pointer variable to node head,p,q explain:
struct node *head,*p,*q;
Generate single linked list:
1.LIFO table:( head (insert after)
head=malloc(sizeof(struct node)) //There can also be no forced type conversion in the front, and the equation will be automatically converted to the data type on the left
tail=head
p1=malloc(sizeof(struct node))
tail->next=p1 //You can assign a value to the data field of p in combination with the scanf function
tail=p1
p2=malloc(sizeof(struct node))
tail->next=p2 //You can also write P1 - > next = P2 without tail
tail=p2
..........
tail->next=NULL; //or pn=NULL
2.First in then out:( head Front (insert)
head=(struct node *)malloc(LENG); //Generate header node
head->next=NULL; //Set as empty table
p=(struct node *)malloc(LENG);//Generate new node
scanf("%d",&e);
p->data=e; //Input data to send the data of the new node
p->next=head->next; //The new node pointer points to the original first node
head->next=p; //The pointer of the header node points to the new node
scanf("%d",&e); //Enter another number
return head; //Return header pointer
}
Various basic operations:
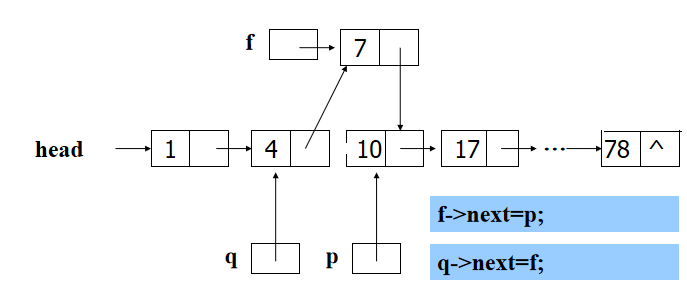
1.Insert: f=(struct node *)malloc(LENG); //generate f->data=x; //Load element x f->next=p->next; //The new node points to the successor of p p->next=f; //The new node becomes the successor of p 2.Delete: q->next=p->next; free(p);
- The function based on basic operation has been realized
- Example: suppose there is an incrementally sorted linked list without header node, insert a new node to make it still increment.
- Algorithm 1: generate an incremental ordered single linked list without leading nodes: ① insert an empty table; ② Tail insertion; ③ Head insertion; ④ General insertion.
struct node * creat3_1(struct node *head,int e)
{ q=NULL; p=head; //q. Insert pointer (P) to scan the position, not to
while (p && e>p->data) //Not finished scanning, and e is greater than the current node
{ q=p; p=p->next;} //q. P move back and check the next position
f=(struct node *)malloc(LENG); //Generate new node
f->data=e; //Load element e
if (p==NULL){
f->next=NULL;
if (q==NULL) //(1) Insert empty table
head=f;
else q->next=f;} //(2) Insert as the last node
else if (q==NULL) //(3) Insert as first node
{f->next=p; head=f;}
else
{f->next=p; q->next=f;} //(4) Generally, insert a new node
return head; }
- Algorithm 2: generate an incremental ordered single linked list of leading nodes
here q Can not be empty, omit the information about in algorithm 1 q of if sentence
void creat3_2(struct node *head,int e)
{ q=head;
p=head->next; //q. P scan to find the insertion position
while (p && e>p->data) //Not finished scanning, and e is greater than the current node
{ q=p;
p=p->next; //q. P move back and check the next position
}
f=(struct node *)malloc(LENG); //Generate new node
f->data=e; //Load element e
f->next=p; q->next=f; //Insert new node
//(2) is also included here as the last node insertion, because the statement F - > next = P does not affect the result
} It can be seen that the header node is wise! (generally, linked lists are owned by default)
- Algorithm 3: insert a new element at the specified position in the single linked list (specified position - no pq positioning)
There is no need to consider the first insertion, F - > next = P - > next; p->next=f; Can include all
int insert( Linklist &L,int i, ElemType e)
{p=L;
j=1;
while (p && j<i)
{ p=p->next; //p moves back to the next position
j++;}
if (i<1 || p==NULL) //Insertion point error
return ERROR;
f=(LinkList) malloc(LENG); //Generate new node
f->data=e; //Load element e
f->next=p->next; p->next=f; //Insert new node
return OK;
}
- Example: delete a node in the single linked list
- Algorithm 1: delete the node with element value e in the single linked list with header node (there can be multiple nodes)
int Delete1(Linklist head, ElemType e)
{ struct node *q,*p;
int result=Yes;
q=head; p=head->next; //q. P scan
while(p)
{
while(p&&p->data!=e) //Find the node with element e
{
q=p; //Remember that you may want to delete the previous node p of the element
p=p->next; //Find next node
}
if (p) //There are nodes with element e
{
q->next=p->next; //Delete this node
free(p); //Free up space occupied by nodes
p=q->next; //p points to the next node
result=Yes;
}
}
return result;
- Algorithm 2: delete the element at the specified position in the single linked list
int Delete2( Linklist &L,int i,ElemType &e)
{p=L;
j=1;
while (p->next && j<i) //p cannot be empty at the end of the loop
{ p=p->next; //p moves back to the next position
j++;}
if (i<1 || p->next==NULL) //Delete point error
return ERROR;
q=p->next; //q points to delete node for free
p->next=q->next; //Extract from the linked list
e=q->data; //Retrieve data element value record
free(q); //Free node space
return OK;
}
About single linked list evaluation:
- advantage:
- When nodes are found, inserting and deleting elements is faster than sequential tables
- No pre allocated space is required, and the number of elements is not limited
- Disadvantages:
- Finding the data elements of a node is slower than the sequential table
2. Static linked list:
- And a linked list described by an array
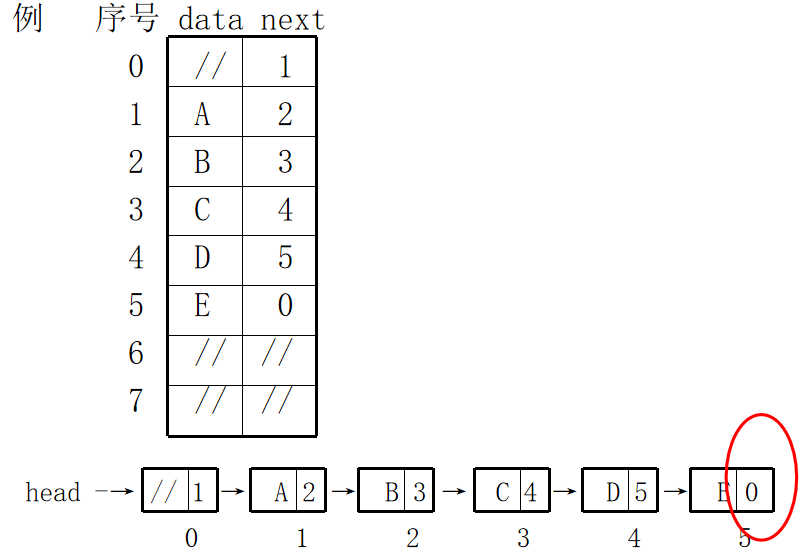
typedef struct //Definition of static linked list
{
int data; //Data in static linked list nodes
int cur; //Cursors in static linked list nodes
}component;
component a[100];
Evaluation of static linked list:
- advantage
- In the insertion and deletion operations, only the cursor needs to be modified without moving elements, which improves the disadvantage that the insertion and deletion operations in the sequential storage structure need to move a large number of elements
- shortcoming
- The problem that it is difficult to determine the table length caused by continuous storage allocation (array) is not solved.
- Lost the random access characteristics of sequential storage structure.
Circular linked list:
-
Non empty circular single linked list with header node
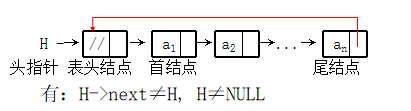
-
Empty circular single linked list with header node
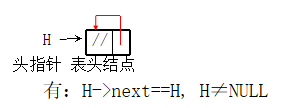
-
Circular linked list with tail pointer only
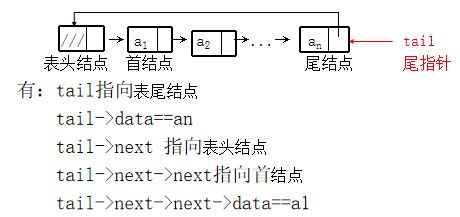
-
Circular null table with tail pointer only
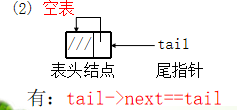
- When using circular linked list, tail pointer is also advocated. It can save the time of finding the tail node in some operations (for example, the first part of two circular linked lists is connected), so as to reduce the time complexity.
- Some algorithms of circular linked list:
- Find the length of the circular single linked list with head as the head pointer, and output the values of nodes in turn.
int length(struct node *head)
{ int leng=0; //The initial value of the length variable is 0
struct node *p;
p=head->next; //p points to the first node
while (p!=head) //p is not moved back to the header node
{ printf("%d",p->data);//output
leng++; //count
p=p->next;} //p move to the next node
return leng; //Return length value
}
Evaluation of circular linked list:
- advantage:
- It is further improved on the basis of single linked list. When traversing, it can start from any node, which increases the flexibility of traversal.
- Disadvantages:
- It does not solve the problem of slow lookup of elements in single linked list
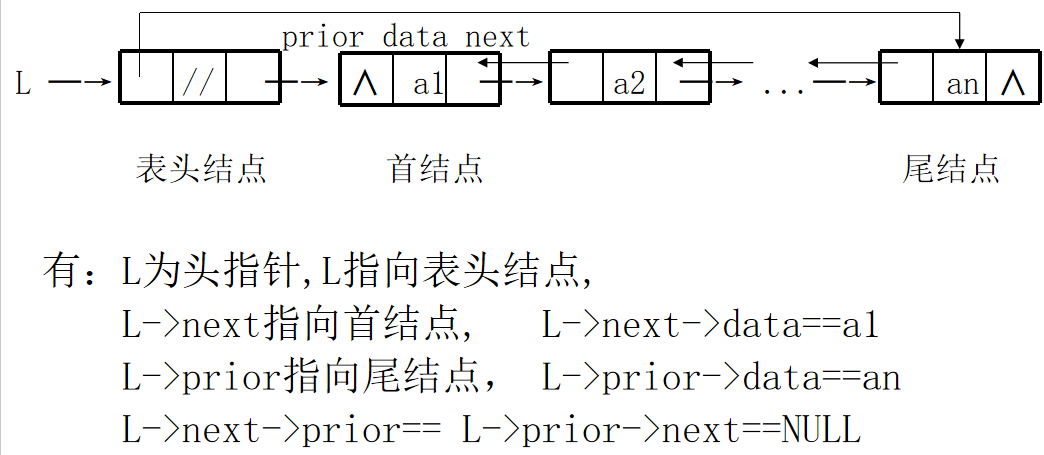
Two way linked list:
- Structure of bidirectional linked list

1. Non empty two-way linked list
2. Empty table

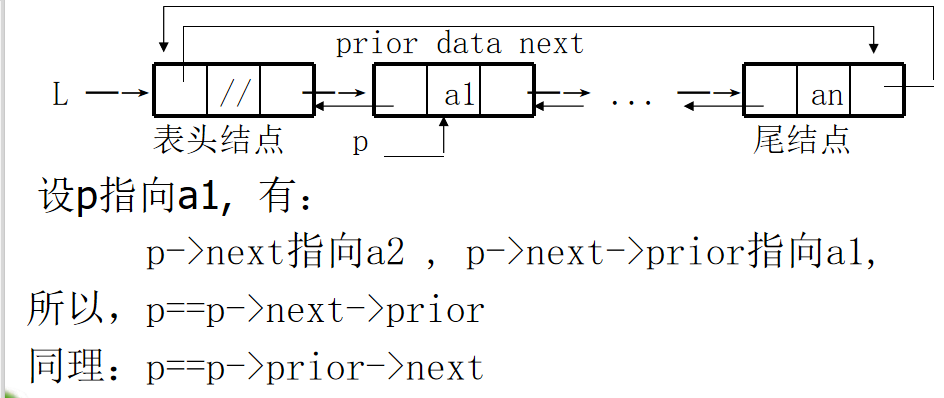
3. Bidirectional circular linked list
4. Empty table

- Basic operation of circular linked list
definition:
typedef struct Dnode
{ ElemType data; //data is an abstract element type
struct Dnode *prior,*next; //Prior and next are pointer types
}*DLList //DLList is a pointer type
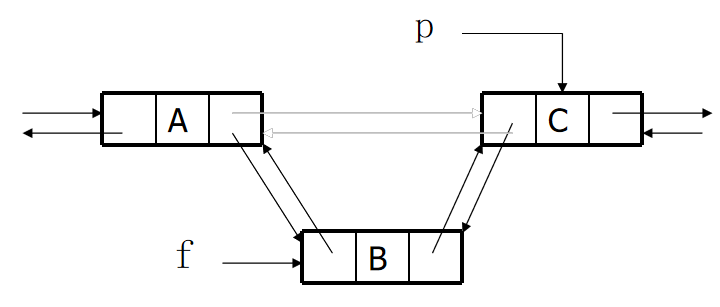
1.insert
f->prior=p->prior; //The prior ity of node B points to node A
f->next=p; //The next of node B points to node C
p->prior->next=f; //The next of node A points to node B
p->prior=f; //The prior ity of node C points to node B
2.delete
p->prior->next=p->next; //The next of node A points to node C
p->next->prior=p->prior; //The prior ity of node C points to node A
free(p); //Release the space occupied by node B
Insert:
Delete: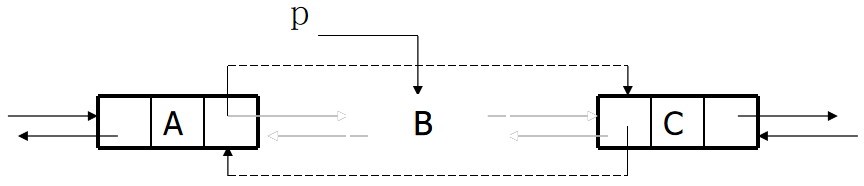
Evaluation of two-way linked list:
- advantage
- Improved on the basis of single linked list, the search element can be searched in both directions, which improves the time required to find an element to a certain extent
- shortcoming
- The need to record prefix points increases the overhead of additional memory space