Chain storage structure: the location of nodes in the memory is arbitrary, that is, logically adjacent data elements are not necessarily adjacent physically. It is also called non sequential image or chain image

Implementation: a group of storage units with arbitrary physical location are used to store the data elements of the linear table. This group of storage units can be continuous or discontinuous.

Related concepts:         Nodes: storage images of data elements= Data field + pointer field

                            Linked list: n nodes are composed of pointer chains

Single linked list: the node has only one pointer field

Double linked list: the node has two pointer fields (one before and one after)

Circular linked list: end to end

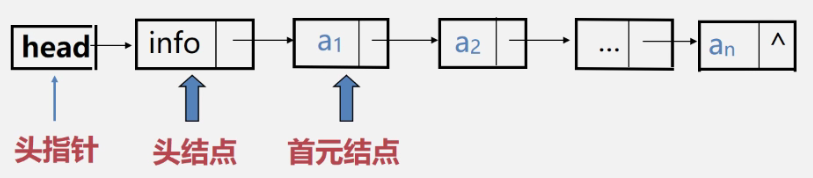
         Header pointer: pointer to the first node of the linked list

         Initial node: the node that stores the first data element a1

         Header node: the node before the initial node

Benefits of setting header nodes

        Easy to handle primitive nodes (no special processing required)

        Easy to handle empty and non empty tables

The data of the header node can be empty or can store additional information such as table length. The header node cannot be included in the table length

characteristic:       The storage location of nodes is arbitrary

                Access can only enter the linked list from the head pointer, and scan backward through the pointer field of each node

definition

tyoedef struct Lnode{
    ElemType data;
    struct Lnode *next;
}Lnode,*LinkList    //LinkList is the pointer type to the structure Lnode

        Define linked list L:         LinkList L;

        Define node pointer P: Lnode *P;

Empty table creation (initialization)

Status InitList(LinkList &L){
    L = new LNode;    //Or L = (LinkList) mallco (sizeof(LNode));
    L->next = NULL;    //Null pointer field
    return OK;
}

Destroy linked list (release in sequence)

Status DesToryList(LinkList &L){
    Lnode *p;
    while(L)//Judge whether L is empty
    {
        p=L;
        L=L->next;
        delete p;
    }
}

Clear the linked list (save the header node and header pointer)

Status ClearList(LinkList &L){
    Lnode *p,*q;
    p=l->next;
    while(p){
        q=p->next;
        delete p;
        p=q;
    }
    L->next=NULL;//Null header pointer
}

Length of linked list

int ListLength(LinkList L){
    LinkList p;
    p=L->next;
    i=0;
    while(p){
        i++;
        p=p->next;
    }
}

Value (take the ith element from the linked list)

Stauts GetElem(LinkList L,int i,ElemType &e){
    p=L->next; j=1;//initialization
    while(p&&j<i)    //Scan linked list < p points to the ith element / P is empty >
    {
        p=p->next;    ++j;
    }
    if(!p || j>i)    return ERROR;//The ith element does not exist
    e=p->data;
    return OK;
}

Value (search by value)

int LocateElem(LinkList L,ElemType e){
    p=L->next;    j=1;
    while(p && p->data=e)
    {p=p->next; j++}
    if(p) return j;//Find data
    else return 0;//No data found
}

Insert data by location

Stauts ListInsert(LinkList &L,int i,ElemType e){
    p=L;    j=0;
    while(p && j<i-1){ p=p->next; ++j;}//Find the i-1 node
    if(!p || j>i-1) return ERROR;?/i Greater than the table length or less than 1, the insertion position is illegal

    s = new LNode;    s->data=e;//Generate nodes and assign data
    s->next=p->next;//Connect successor pointer
    p->next=s;//Connection precursor pointer

    return OK;
}

Delete data by location

Status ListDelete(LinkList &L,int i,ElemType &e){
    p=L;  j=0;
    while(p->next && j<i-1){ p=p->next; ++j; }//Find the ith node and point p to its precursor
    if(!(p->next) || j>i-1) return ERROR;//Unreasonable deletion position

    q=p->next;//Zero time variable (bind the node to be deleted and prepare to release)
    p->next=q->next;//Disconnect nodes
    e=q->next;//Save data
    delete q;//Delete data
    return OK;
}

Time efficiency of insertion, deletion and search algorithms

        Find o

        Insert and delete: there is no need to move the element, only need to modify the pointer. The time complexity is O(1), but the time complexity to find the node at the corresponding position is O(n)

Establishment of linked list

        Header insertion (insert elements into the header of the linked list)

void CreateList_H(LinkList &L,int n)
{
    L=new LNode;
    L->next=NULL;
    for(i=n;i>0;i++)
    {
        p=new LNode;// p =(LNode*) mallco (sizeof(LNode));
        cin>>p->data;
        p->next=L->next;//Insert element into header
        L->next=p;//Connector pointer
    }
}

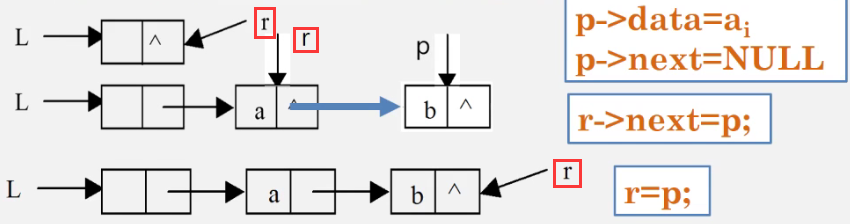
        Tail inserting method (element inserting tail)

void CreateList_R(LinkList &L,int n)
{
    L=new LNode;    L->next=NULL;
    r=L;//The tail pointer r points to the head node
    for(i=0;i<n;++i){
        p=new LNode;    cin>>p-data;//Generate node, set value

        p->next=NULL;
        r->next=p;
        r->next=p;//Insert to footer
        r=p;//r points to the new tail node
    }
}

        The auxiliary pointer r always points to the end of the queue (as shown in the figure)