Data structure and algorithm notes 1 (python)

Posted by TalonFinsky on Tue, 19 Oct 2021 01:18:14 +0200

Data structure and algorithm notes 1 (python)

Proposed algorithm

Concept of algorithm

Algorithm is the essence of computer processing information, because computer program is essentially an algorithm to tell the computer the exact steps to perform a specified task. Generally, when the algorithm is processing information, it will read the data from the input device or the storage address of the data, and write the result to the output device or a storage address for later call.

Algorithm is an independent method and idea to solve problems.

For the learning algorithm, the important thing is the idea, and the implementation is the second.

The algorithm can be implemented in many different languages, such as c/c++/java/python, etc. this note mainly uses Python to describe and implement.

Before the specific study, we can introduce the understanding of the concept of algorithm through a simple topic that can be understood by the knowledge level of junior middle school.

# If a+b+c=N and a^2+b^2=c^2 (a, b and c are natural numbers), how to find all possible combinations of a, b and c?

import time

start_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a + b + c == 1000 and a**2 + b**2 == c**2:
                print("a, b, c:%d, %d, %d" % (a, b, c))
end_time = time.time()
print("times:%d" % (end_time - start_time))
print("finished 0")

a, b, c:0, 500, 500
a, b, c:200, 375, 425
a, b, c:375, 200, 425
a, b, c:500, 0, 500
times:107
finished 0


# T = 1000 * 1000 * 1000 * 10
# T = N * N * N * 10
# T(n) = n ^ 3 * 10
#We often only analyze a general feature, and the same order of magnitude can be approximately equal to
#After omission
# T(n) = n ^ 3 * 2
#Finally, it can be considered that the time complexity is
# T(n) = O(n ^ 3)

start_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c:%d, %d, %d" % (a, b, c))
end_time = time.time()
print("times:%d" % (end_time - start_time))
print("finished 1")

a, b, c:0, 500, 500
a, b, c:200, 375, 425
a, b, c:375, 200, 425
a, b, c:500, 0, 500
times:0
finished 1


# T(n) = O(n ^ 2)

# The total execution time of each machine is different
# However, the number of basic operations performed is roughly the same
# Total time = time of each step * number of steps

Through the comparison of the two codes, we can clearly see that the running time of the same subject can differ by several orders of magnitude with only a small change. Therefore, it is very necessary to optimize the algorithm of the same problem.

Five characteristics of the algorithm

Input: the algorithm has 0 or more inputs
Output: the algorithm has at least one or more outputs
Boundedness: the algorithm will automatically end after a limited number of steps without infinite loops, and each step can be completed in an acceptable time
Certainty: every step in the algorithm has a definite meaning, and there will be no ambiguity
Feasibility: each step of the algorithm is feasible, that is, each step can be completed a limited number of times

Algorithm efficiency measurement

Execution time response algorithm efficiency

For the same problem, we give two algorithms. In the implementation of the two algorithms, we calculate the execution time of the program and find that the execution time of the two programs is very different. Therefore, we can draw a conclusion: * * the execution time of the algorithm program can reflect the efficiency of the algorithm, that is, the advantages and disadvantages of the algorithm** However, the operation of the program is inseparable from the computer environment (including hardware and operating system). These objective reasons will affect the speed of the program and reflect on the execution time of the program.

Note: simply relying on the running time to compare the advantages and disadvantages of the algorithm is not necessarily objective and accurate!

Suppose we run the two codes on an antique computer decades ago, the running time may not be very different.

Time complexity and "Big O notation"

We assume that the time for the computer to perform each basic operation of the algorithm is a fixed time unit, so how many basic operations represent how many time units it will take. However, for different machine environments, the exact unit time is different, but the number of basic operations (i.e. how many time units it takes) of the algorithm is the same in the order of magnitude. Therefore, the influence of the machine environment can be ignored and the time efficiency of the algorithm can be reflected objectively.

The time efficiency of the algorithm can be expressed by "Big O notation".

"Large o notation": for monotonic integer function f, if there is an integer function g and real constant C > 0, so that for sufficiently large N, there is always f (n) < = C * g (n), that is, function g is an asymptotic function of F (ignoring the constant), which is recorded as f(n)=O(g(n)). In other words, in the sense of the limit towards infinity, the growth rate of function f is constrained by function g, that is, the characteristics of function f and function g are similar.

Time complexity: assuming that there is A function g such that the time taken by algorithm A to deal with the problem example with scale n is T(n)=O(g(n)), then O(g(n)) is called the asymptotic time complexity of algorithm A, referred to as time complexity for short, and recorded as T(n)

How to understand "big notation"

For the temporal and spatial properties of the algorithm, the most important is its order of magnitude and trend. The constant factors in the scale function of the basic operation quantity of the measurement algorithm can be ignored. For example, it can be considered that 3*n2 and 100*n2 belong to the same order of magnitude. If the cost of the two algorithms for processing instances of the same size is these two functions respectively, their efficiency is considered to be "almost" and both are n^2.

Worst time complexity

There are several possible considerations when analyzing the algorithm:

How many basic operations does the algorithm need to complete the work, that is, the optimal time complexity
How many basic operations does the algorithm need to complete the work, that is, the worst time complexity
The average number of basic operations required for the algorithm to complete the work, that is, the average time complexity

For the optimal time complexity, it is of little value because it does not provide any useful information. It only reflects the most optimistic and ideal situation, and has no reference value.

For the worst time complexity, it provides a guarantee that the algorithm can complete the work in this level of basic operation.

The average time complexity is a comprehensive evaluation of the algorithm, so it completely reflects the properties of the algorithm. On the other hand, there is no guarantee that not every calculation can be completed within this basic operation. Moreover, it is difficult to calculate the average case because the instance distribution of the application algorithm may not be uniform.

Therefore, we mainly focus on the worst case of the algorithm, that is, the worst time complexity.

Several basic calculation rules of time complexity

The basic operation, that is, there is only a constant term, is considered to have a time complexity of O(1)
Sequential structure, and the time complexity is calculated by addition
Loop structure, and the time complexity is calculated by multiplication
Branching structure, the time complexity is the maximum
When judging the efficiency of an algorithm, we often only need to pay attention to the highest order term of the number of operations, and other secondary terms and constant terms can be ignored
Without special instructions, the time complexity of the algorithm we analyze refers to the worst time complexity

Now, we can analyze our two codes through the above concepts

Code 1:

for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a + b + c == 1000 and a**2 + b**2 == c**2:
                print("a, b, c:%d, %d, %d" % (a, b, c))

The time complexity is: T(n) = O(n * n * n) = O(n^3)

Code 2:

for a in range(0, 1001):
    for b in range(0, 1001):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c: %d, %d, %d" % (a, b, c))

The time complexity is: t (n) = O (n * n * (1 + 1)) = O (n * n) = O (n ^ 2)

It can be seen that the second algorithm we try is much more time complex than the first algorithm.

Common time complexity

Example of execution times function	rank	informal term
12	O(1)	Constant order
2n+3	O(n)	Linear order
3n2+2n+1	O(n2)	Square order
5log2n+20	O(logn)	Logarithmic order
2n+3nlog2n+19	O(nlogn)	nlogn order
6n3+2n2+3n+4	O(n3)	Cubic order
2n	O(2n)	Exponential order

Note that log2n (base 2 logarithm) is often abbreviated to logn

Relationship between common time complexity

[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-zosvmkpj-1634550533157)( file:///C:/Users/%E5%BC%A0%E6%99%A8%E6%9B%A6/Desktop/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E9%A2%84%E7%AE%97%E6%B3%95%E8%AF%BE%E4%BB%B6/images/ Algorithm efficiency relationship (. bmp)]

Time consumed from small to large:

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

Python built-in type performance analysis

timeit module

The timeit module can be used to test the execution speed of a small piece of Python code.

class timeit.Timer(stmt = 'pass', setup = 'pass' , timer = < timer function >)

Timer is a class that measures the execution speed of small pieces of code.

stmt parameter is the code statement to be tested;

The setup parameter is the setting required to run the code;

The timer parameter is a timer function, which is platform related.

timeit.Timer.timeit(number=1000000)

The object method in the Timer class that tests the execution speed of statements. The number parameter is the number of tests when testing the code. The default is 1000000. Method returns the average time spent executing code, in seconds of a float type.

list operation test

from timeit import Timer
# li1 = [1, 2]
# li2 = [23,5]
# li = li1+li2
# li = [i for i in range(10000)]
# li = list(range(10000))

# def t1():
#     li = []
#     for i in range(10000):
#         li.append(i)
#
# def t2():
#     li = []
#     for i in range(10000):
#         li = li + [i]
#         # li += [i]
#
# def t3():
#     li = [i for i in range(10000)]
#
# def t4():
#     li = list(range(10000))
#
# def t5():
#     li = []
#     for i in range(10000):
#         li.extend([i])
#
# timer1 = Timer("t1()", "from __main__ import t1")
# print("append:", timer1.timeit(1000))
#
# timer2 = Timer("t2()", "from __main__ import t2")
# print("+:", timer2.timeit(1000))
#
# timer3 = Timer("t3()", "from __main__ import t3")
# print("[i for i in range]:", timer3.timeit(1000))
#
# timer4 = Timer("t4()", "from __main__ import t4")
# print("list(range()):", timer4.timeit(1000))
#
# timer5 = Timer("t5()", "from __main__ import t5")
# print("extend:", timer5.timeit(1000))

# append: 0.5859431
# +: 151.9984935
# [i for i in range]: 0.2666621000000191
# list(range()): 0.11709400000000869
# extend: 0.8316012999999884

def t6():
    li = []
    for i in range(10000):
        li.append(i)

def t7():
    li = []
    for i in range(10000):
        li.insert(0, i)


timer6 = Timer("t6()", "from __main__ import t6")
print("append", timer6.timeit(1000))

timer7 = Timer("t7()", "from __main__ import t7")
print("insert(0)", timer7.timeit(1000))

# append 0.6039895000000001
# insert(0) 21.2750359

pop operation test

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")

# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

It can be seen from the results that the efficiency of the last element of pop is much higher than that of the first element of pop

Time complexity of list built-in operations

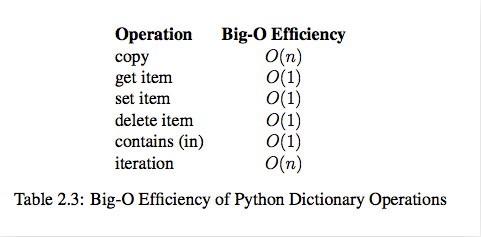
Time complexity of built-in operation of dict

Topics: Python Algorithm data structure

Programmer Think

Data structure and algorithm notes 1 (python)

Data structure and algorithm notes 1 (python)

Proposed algorithm

Concept of algorithm

Five characteristics of the algorithm

Algorithm efficiency measurement

Execution time response algorithm efficiency

Time complexity and "Big O notation"

How to understand "big notation"

Worst time complexity

Several basic calculation rules of time complexity

Common time complexity

Relationship between common time complexity

Python built-in type performance analysis

timeit module

Time complexity of list built-in operations

Time complexity of built-in operation of dict

Hot Topics