1, Hanoi Tower problem

def hanoi(n,a,b,c):  #Move from a through b to c
    if n>0:
        hanoi(n-1,a,c,b) #Move from a through b to c
        print("disc%d moving from %s to %s" %(n,a,c))
        hanoi(n-1,b,a,c)  #Move from b through a to c

hanoi(2,'A','B','C')

The recurrence formula h(x)=2h(x-1)+1 is about equal to the nth power of 2

2, Search

1. Sequential search

def linear_search(li,val):
    for ind,v in enumerate(li):
        if v == val:
            return ind
    else:
        return None

2. Dichotomy search

def binary_search(li,val):
    left = 0
    right = len(li) - 1
    while left <= right:  #Candidate area has value
        mid = (left + right) // 2 # divide by 2
        if li[mid] == val:
            return mid
        elif li[mid] > val:  #The value to be found is to the left of mid
            right = mid - 1
        else:               #The value to be found is to the right of mid
            left = mid + 1
    else:
        return None  #Not found

Time complexity: O(logn)

3, Sort

Primary sort:

1. Bubble sorting

Sorting in place does not need to occupy new memory space.

Every two adjacent numbers in the list. If the front is larger than the back, exchange these two numbers;

After a sequence is completed, the unordered area decreases by one number and the ordered area increases by one number.

def bubble_sort(li):  #Ascending arrangement
    for i in range(len(li)-1):  #The i-th trip starts from 0
         exchange = False
         for j in range(len(li)-i-1):  #Pointer, n-i-1 positions per trip
             if li[j] > li[j+1]:
                 li[j],li[j+1] = li[j+1],li[j]
                 exchange = True
         print(li)
         if not exchange:
             return

Time complexity O(n^2)

2. Select sort

The minimum number of records to be sorted in a row is placed in the first position

Once again, sort the smallest number in the unordered area of the record list and put it in the second position

... until the end of sorting

def select_sort(li):
    for i in range(len(li)-1):  #Trip i
        min_loc = i
        for j in range(i+1,len(li)):  #Traversal range
            if li[j] < li[min_loc]:  #If it is the smallest, save the subscript to min_loc
                min_loc = j
        li[i],li[min_loc] = li[min_loc],li[i]  #The minimum value and the first number of disordered areas exchange positions
        print(li)

Time complexity O(n^2)

3. Insert sort

At the beginning, there is only one card in your hand (ordered area)

Touch a card from the disordered area each time and insert it into the correct position of the existing card in your hand

def insert_sort(li):
    for i in range(1,len(li)):  #Indicates the subscript of the touched card
        tmp = li[i]
        j = i - 1  #j refers to the subscript of the card in hand traversing from right to left
        while li[j] > tmp and j >= 0:  #Until you find a card smaller than the one you touch
            li[j+1] = li[j]  #Move one bit to the right
            j -= 1
        li[j+1] = tmp
        print(li)

Time complexity O(n^2)

Advanced sort:

3. Quick sort

Take the first element p (the first element) and return the element p

The list is divided into two parts by p. the left is smaller than p and the right is larger than p

Recursive completion sorting

def partition(li,left,right):#One time fast sorting of homing function
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:  #From the right, find a number smaller than tmp and put it in the space of left
             right -= 1   #One to the left
        li[left] = li[right]  #Put the value on the right into the space on the left

        while left < right and li[left] <= tmp:
            left += 1
        li[right] = li[left]  #Put the value on the left into the space on the right
    li[left] = tmp  #Reset the original value
    return left  #Put back mid, that is, the value of left or right


def quick_sort(li,left,right):
    if left < right:   #There are at least two elements
        mid = partition(li,left,right)
        quick_sort(li,left,mid-1)
        quick_sort(li,mid+1,right)   #Recursive call mid is divided into left and right parts

Time complexity: O(nlogn)

Worst case: O(n^2)

Avoidance method: you can mess up the list first, or select the first number at random instead of the first number

4. Heap sort

Storage mode of binary tree: chain storage mode and sequential storage mode

Sequential storage mode:

Parent node i, left child node 2i+1, right child node 2i+2

Child node i, parent node (i-1) // 2

Heap: is a special complete binary tree structure

Large root heap: a complete binary tree that satisfies that any node is larger than its child node

Small root heap: a complete binary tree, satisfying that any node is smaller than its child node

One-time downward adjustment: the left and right subtrees of a node are heaps, but they are not heaps. They can be turned into a heap by one-time downward adjustment

Heap sort process:

(1) Build heap (any node is larger / smaller than its child node)

(2) Start counting by size: get the top element of the heap, which is the largest element

(3) Remove the top of the heap and put the last element of the heap on the top of the heap. At this time, the conditions for one-time downward adjustment are met, and the heap can be reordered through one-time adjustment

(4) The top element is the second largest element

(5) Repeat step 3 until the reactor becomes empty

Build heap:

First look at the last non leaf node and look up layer by layer

def sift(li,low,high):   #One time downward adjustment algorithm
    """
    :param li: list
    :param low: Heap top position of the heap (root node)
    :param high: Position of the last element of the heap
    :return:
    """
    i = low   #i initially points to the root node
    j = 2 * i + 1  #j started as a left child
    tmp = li[low]  #Store the top of the pile
    while j <= high:  #Cycle as long as there are several j positions
        if j+1 <= high and li[j+1] > li[j]:  #If the right child is larger than the left child, point j to the right child
            j = j + 1   #Point j to the right child
        if li[j] > tmp:
            li[i] = li[j]  #Move the large number to the position of i
            i = j   #i look down one floor
            j = 2 * i + 1
        else:   #tmp is bigger. Put tmp at i
            li[i] = tmp  #Put tmp in the position of the parent node of a certain layer
            break
    else:
        li[i] = tmp  #j> After high, put the tmp into the leaf node


def heap_sort(li):
    n = len(li)
    #Build heap
    for i in range((n-2)//2,-1,-1):
        #i represents the subscript of the root of the adjusted part when creating the heap, starting from the root node of n-1, in reverse order
        sift(li,i,n-1)  #low is the root node of the adjustment part, and high is placed directly on the last leaf node
    #Heap building is complete and counting begins
    for i in range(n-1,-1,-1):
        #i always points to the last number in the heap
        li[0],li[i] = li[i],li[0]  # The last number is exchanged with the top of the heap
        sift(li,0,i-1)  #Adjust the low of the whole heap to 0, the current last number is i-1, and i-1 is the new high
    #Sort complete

li = [i for i in range(100)]
import random
random.shuffle(li)
print(li)
heap_sort(li)
print(li)

Time complexity: half the complexity of sift process, which is O(logn); Entire heap sort O(nlogn)

Actual performance: quick sort is better than heap sort

Python heap sorting built-in module: heapq

Common functions:

Heap ify (x): build heap (small root heap)

heappush(heap,item): add elements to heap

heappop(heap): pop up a minimum number at a time

eg:

import heapq   #Q - > queue priority queue (small first out / large first out)
import random

li = [i for i in range(100)]
random.shuffle(li)

print(li)
heapq.heapify(li)  #Build pile
print(li)

for i in range(len(li)):
    print(heapq.heappop(li),end=',')

topk problem: there are n numbers. Design the algorithm to get the number with the largest top k (k < n)

Solution:

Slice after sorting O(nlogn)

Bubble / insert / select sort O(kn)

Using heap sorting: complexity O(nlogk) is faster

Take the first k elements of the list to create a small root heap, and the top of the heap is the largest number k at present

Traverse the original list backward in turn. If the element in the list is less than the top of the heap, the element is ignored; If it is larger than the top of the heap, replace the top of the heap with this element and adjust the heap once

After traversing all the elements in the list, pop up the top of the heap in reverse order

#topk changes according to heap sort
def sift(li,low,high):   #One time downward adjustment algorithm
    """
    :param li: list
    :param low: Heap top position of the heap (root node)
    :param high: Position of the last element of the heap
    :return:
    """
    i = low   #i initially points to the root node
    j = 2 * i + 1  #j started as a left child
    tmp = li[low]  #Store the top of the pile
    while j <= high:  #Cycle as long as there are several j positions
        if j+1 <= high and li[j+1] < li[j]:  #If the right child is smaller than the left child, point j to the right child
            j = j + 1   #Point j to the right child
        if li[j] < tmp:
            li[i] = li[j]  #Move the small number to the position of i
            i = j   #i look down one floor
            j = 2 * i + 1
        else:   #tmp is bigger. Put tmp at i
            li[i] = tmp  #Put tmp in the position of the parent node of a certain layer
            break
    else:
        li[i] = tmp  #j> After high, put the tmp into the leaf node


def topk(li,k):
    heap = li[0:k]
    for i in range((k-2)//2,-1,-1):
        sift(li,i,k-1)
    #1. Build pile
    for i in range(k,len(li)-1):
        if li[i] > heap[0]:
            heap[0] = li[i]
            sift(heap,0,k-1)
    #2. Traverse all elements
    for i in range(k-1,-1,-1):
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i - 1)
    #3. Count out
    return heap


import random
li = list(range(100))
random.shuffle(li)

print(topk(li,10))

5. Merge sort

One time merge: suppose the list is divided into two ordered segments, which are collectively called a sequential table

Merge sort - use one merge:

(1) Decomposition: divide the list smaller and smaller until it is divided into one element

(2) Termination condition: when there is only one element, it must be ordered

(3) Merge: merge two sequential tables. The list becomes larger and larger

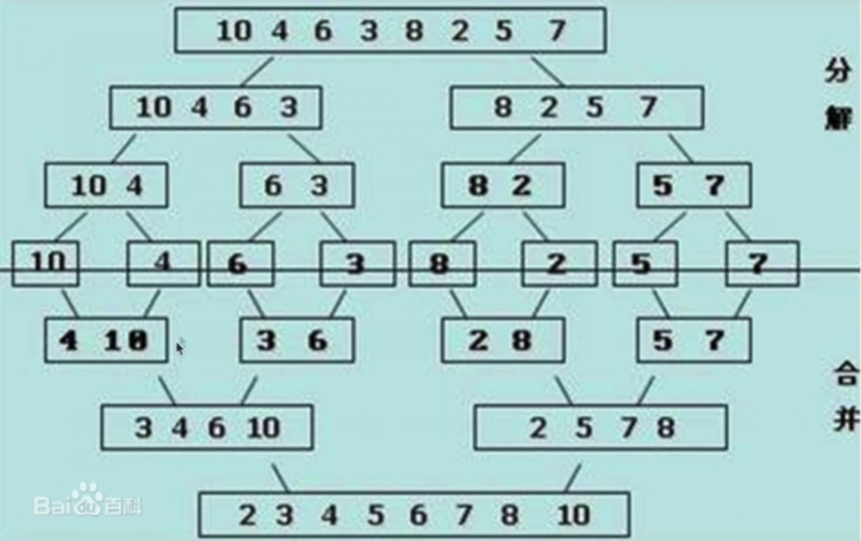
def merge(li,low,mid,high): #The list is divided into two paragraphs
    i = low
    j = mid + 1   #Start pointer at both ends
    ltmp = []  #A temporary list
    while i <= mid and j <= high:  #As long as there are both left and right paragraphs
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    #After the while execution, some of the two paragraphs must be numbered
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp   #Slice the right package and write the temporary list


def merge_sort(li,low,high):
    if low < high:   #There are at least two elements in the segment, recursive
        mid = (low + high) //2
        merge_sort(li,low,mid)
        merge_sort(li,mid+1,high)
        merge(li,low,mid,high)

Time complexity: once merge O(n), decompose + merge the whole: O(nlogn)

Space complexity: O(n) opens temporary list storage