Data structure and algorithm tree
Previous contents
1 - linked list
2-stack and queue
3-string
4-tree
5-fig
8-sort
9 - query
6-greedy algorithm
7-recursion and divide and conquer
10 - dynamic programming
11-STL Library
Common sorting algorithms
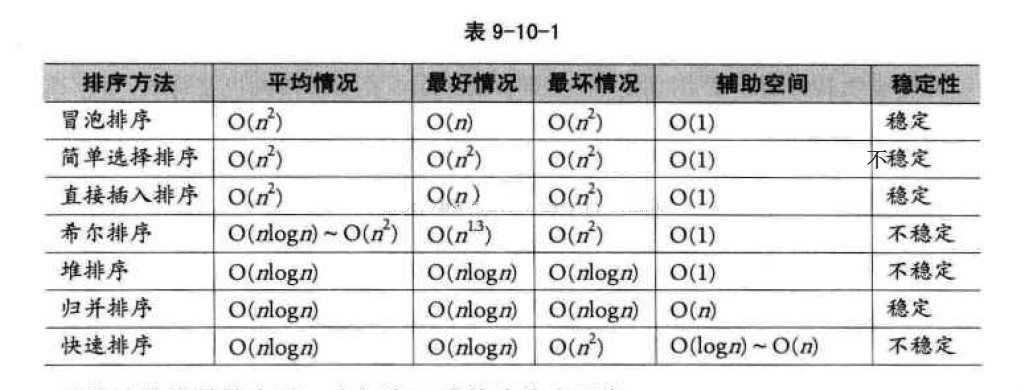
Unstable algorithms: quick sort, Hill sort, selective sort, heap sort
1. Bubble sorting
1.1 bubble sorting (exchange) of low configuration version
void BubbleSort(int *arr,int length)
{
for(int i=0;i<length;i++)
{
for(int j=i+1;j<length;j++)
{
if(arr[i]>arr[j])
{
int temp=arr[j];
arr[j]=arr[i];
arr[i]=temp;
}
}
}
}
1.2 bubble sorting
- Note: the second for loop j=length-i-1; It must be noted that there is also a - 1, because for N data, it only needs to be compared n-1 times, so - 1 is required
void BubbleSort1(int arr[],int length)
{
for(int i=0;i<length;i++)
{
for(int j=0;j<length-i-1;j++)
{
if(arr[j]>arr[j+1])
{
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}
1.3 bubble sorting optimization 1
- Set a flag bit flag, but if there is no exchange at one time, it indicates that the sorting has been completed
void BubbleSort2(int arr[],int length)
{
bool flag=true;//Do you want to continue sorting as long as there is an exchange
for(int i=0;i<length && flag;i++)
{
flag=false;
for(int j=0;j<length-1-i;j++)
{
if(arr[j]>arr[j+1])
{
flag=true;
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}
1.4 bubble sorting optimization 2 - Cocktail sorting
- Also called bidirectional bubbling
Cocktail ranking: from low to high, then from high to low
Bubble sort: from low to high
//4. Cocktail ranking: from low to high, then from high to low
void BubbleSort3(int arr[],int length)
{
int i,temp;
int left,right;
left=0;
right=length-1;
while(left<right)
{
//From back to front
for(i=right;i>left;i--)
{
if(arr[i-1]>arr[i])
{
temp=arr[i];
arr[i]=arr[i-1];
arr[i-1]=temp;
}
}
left++;
//From front to back
for(i=left;i<right;i++)
{
if(arr[i]>arr[i+1])
{
temp=arr[i];
arr[i+1]=arr[i];
arr[i]=temp;
}
}
right--;
}
}
2. Select Sorting
Only the corresponding position is found each time, and the data is exchanged during the second layer cycle
void SelectSort(int *arr,int length)
{
int idcard;//The essence is to find the location first and exchange
for(int i=0;i<length;i++)
{
idcard=i;
for(int j=i+1;j<length;j++)
{
if(arr[idcard]>arr[j])
idcard=j;
}
if(idcard!=i)
{
int temp=arr[idcard];
arr[idcard]=arr[i];
arr[i]=temp;
}
}
}
-Compared with ordinary exchange sorting, it saves each exchange
void SelectSort0(int arr[],int length)
{
for(int i=0;i<length;i++)
{
for(int j=i+1;j<length;j++)
{
if(arr[i]>arr[j])
{
int temp=arr[j];
arr[j]=arr[i];
arr[i]=temp;
}
}
}
}
3. Insert sort
For any low i positions, it is considered that the first i-1 positions are orderly. When the i position is smaller than the previous elements, compare them in turn, and move the positions in turn until the empty position is 0 or meets the conditions. Remember to save the value of the inserted element with a temporary variable.
void InsertSort(int *arr,int length)
{
int target;
for(int i=1;i<length;i++)
{
target=arr[i];
int pos=i;//Where it should be inserted
while(pos>0 && target<arr[pos-1])
{
arr[pos]=arr[pos-1];
pos--;
}
arr[pos]=target;
}
}
- Improved binary insertion sort
//7. Binary insertion sort
void InsertSort1(int arr[],int length)
{
for(int i=1;i<length;i++)
{
if(arr[i]<arr[i-1])
{
int target=arr[i];
int left=0;
int right=i-1;
while(left<=right)
{
int mid=left+(right-left)/2;
if(target>arr[mid])
{
left=mid+1;
}
else
{
right=mid-1;
}
}
for(int j=i;j>left;j--)
{
arr[j]=arr[j-1];
}
arr[left]=target;
}
}
}
4. Hill sort
Hill sort is actually changed based on insertion sort. Hill sort first groups the data, that is, sort the data of gas every interval, and then change the size of gas in turn. gas=1 must be taken for the last time, and the completed insertion sort can be obtained for the last time.
Hill sort reference video
//8. Hill sort
void shellSort(int *arr,int length)
{
int gas=length;//Interval per insert
int target;//Insert sorting data to be arranged temporarily
while(gas>0)
{
//Insert sort section
for(int i=gas;i<length;i++)
{
target=arr[i];
int pos=i;
while(pos>0&& target<arr[pos-gas])//Move data after
//While (POS > = gas & & target < arr [POS gas]) / / move data after
{
arr[pos]=arr[pos-gas];
pos-=gas;
}
arr[pos]=target;
}
gas=gas/2;//Change the interval. When performing insertion sorting, be sure to get 1
//Complete insertion sort
}
}
- Compare insert sort with Hill sort
void InsertSort(int *arr,int length)
{
//int gas=length;
int target;
//while(gas>0)
//{
int gas=1;
for(int i=gas;i<length;i++)
{
target=arr[i];
int pos=i;
while(pos>0 && target<arr[pos-gas])//Move data after
{
arr[pos]=arr[pos-gas];
pos-=gas;
}
arr[pos]=target;
//}
//gas=gas/2;
}
}
5. Heap sorting
Heap sorting is a sort of selection
a. Build the unnecessary sequence into a heap, and select the large top heap or small top heap according to the ascending and descending requirements;
b. Exchange the top element with the end element, and "sink" the largest element to the end of the array;
c. Readjust the structure to meet the heap definition, then continue to exchange the heap top elements with the current tail elements, and repeat the adjustment + exchange steps until the whole sequence is in order.
Reference heap sort
Reference video

void HeapAdjust(int *arr,int begin,int length)
{
int temp=arr[begin];//Keep the first element
for(int i=2*begin+1;i<length;i=i*2+1)//Start from the left child of node i, that is, 2i+1
{
if(i+1<length && arr[i]<arr[i+1])//Take out the larger elements in the left and right children, and the label of the node is i
i++;
if(temp>=arr[i])//temp is the maximum value without adjustment
break;
else
{
arr[begin]=arr[i];//Maximum root
begin=i;//Operate on the maximum position
}
}
arr[begin]=temp;
}
void HeapSort(int *arr,int length)
{
for(int i=length/2-1;i>=0;i--)//Build a large top heap, and [(length-1)/2 starts from the last node with children]
{
HeapAdjust(arr,i,length); //Build the elements of [0,1,2...length] into a large top heap
}
for(int i=length-1;i>0;i--)//Gradually swap each root value with the last element
{
//Exchange data
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
HeapAdjust(arr,0,i);//Reorder the elements of [0,1,2,3...length] by row
}
}
6. Merge and sort
Call in turn
void MergeSort(int arr[],int length);
void MSort(int arr[],int begin,int end);
void Merge(int arr[], int begin,int mid,int end);
MergeSort sort – > msort sort – > merge sort
//=============================Merge sort memory version===========================================
/*
Merge sort is mainly composed of the following three functions
void MergeSort(int arr[],int length);
void MSort(int arr[],int begin,int end);
void Merge(int arr[], int low,int mid,int high);
*/
void Merge3(int arr[],int begin,int mid,int end)
{
int* tempArr=(int *)malloc((end-begin+1)*sizeof(int));
// int length=end-begin+1;
// int tempArr[length];
int i=begin;//First half
int j=mid+1;//Second half
int k=0;//The first half data and the second half data are merged into the subscript of the new array
while(i<=mid && j<=end)
{
if(arr[i]<=arr[j])
{
tempArr[k++]=arr[i++];
}
else
{
tempArr[k++]=arr[j++];
}
}
while(i<=mid)
{
tempArr[k++]=arr[i++];
}
while(j<=end)
{
tempArr[k++]=arr[j++];
}
//Copy the sorted data from tempArr to
//From begin to end
for(i=begin,k=0;i<=end;i++,k++)
{
arr[i]=tempArr[k];
}
delete[] tempArr;
}
void MSort3(int arr[],int begin,int end)
{
if(begin>=end)
return ;
int mid=(begin+end)/2;
MSort3(arr,begin,mid);
MSort3(arr,mid+1,end);
Merge3(arr,begin,mid,end);
}
void Mergesort3(int arr[],int length)
{
MSort3(arr,0,length-1);
}
7. Quick sort
The records to be sorted are divided into two independent parts through one-time sorting, in which the keywords of one part are greater than those of the other part, and then the two parts continue to be sorted, so as to finally achieve the purpose of ordering the whole sequence
Similar to merge sort, the quick sort algorithm is also divided into three parts, which are called in turn
void QuickSort(int arr[],int length);
void QSort(int arr[],int begin,int end);
void Partition(int arr[], int begin,int end);
QuickSort - > qsort - > partition location
int Partition0(int arr[], int begin,int end)
{
int pivotkey=arr[begin];//In fact, the position is used as the pivot
while(begin<end)
{
while(begin<end && arr[end]>=pivotkey)
end--;
//Exchange data
int temp=arr[begin];
arr[begin]=arr[end];
arr[end]=temp;
while(begin<end && arr[begin]<=pivotkey)
begin++;
//Exchange data
temp=arr[begin];
arr[begin]=arr[end];
arr[end]=temp;
}
return begin;
}
//optimization
int Partition(int arr[], int begin,int end)
{
int pivotkey=arr[begin];//In fact, the position is used as the pivot
while(begin<end)
{
while(begin<end && arr[end]>=pivotkey)
end--;
//Exchange data
arr[begin]=arr[end];
while(begin<end && arr[begin]<=pivotkey)
begin++;
//Exchange data
arr[end]=arr[begin];
}
arr[begin]=pivotkey;
return begin;
}
void QSort(int arr[],int begin,int end)
{
int pivot;
if(begin>=end)
return;
pivot=Partition(arr,begin,end);
QSort(arr,begin,pivot-1);
QSort(arr,pivot+1,end);
}
void QuickSort(int arr[],int length)
{
QSort(arr,0,length-1);
}