Algorithm efficiency
Measuring the quality of an algorithm depends on the efficiency of the algorithm, and the efficiency of the algorithm is measured by two dimensions of time and space, namely time complexity and space complexity. Time complexity mainly measures the speed of an algorithm, and space complexity measures the additional space required by the algorithm.
Time complexity
Concept of time complexity
In computer science, the time complexity of an algorithm is a function, which quantitatively describes the running time of the algorithm. The time spent by an algorithm is directly proportional to the execution times of the statements in it. The execution times of the basic operations in the algorithm is the time complexity of the algorithm, which is expressed by the large O progressive representation, which is an estimation representation.
Method of pushing down large O-order
- Replace all addition constants in the running time with constant 1
- In the modified run times function, only the highest order term is retained
- If the highest order term exists and is not 1, the constant multiplied by this item is removed. The result is a large O-order
Example 1
Please calculate how many times the + + count statement in Func1 is executed in total?
void Func1(int N) {
int count = 0;
//Code 1:
for (int i = 0; i < N ; ++ i) {
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
//Code 2:
for (int k = 0; k < 2 * N ; ++ k) {
++count; }
int M = 10;
//Code 3:
while (M--)
{
++count;
}
printf("%d\n", count);
}
In code 1, + count executes N*N times
In code 2, + count executes 2 * N times
In code 3, + count is executed 10 times
Therefore, in Func function, + count executes F(N) = N * N + 2 * N + 10 times
After using the large o asymptotic representation, the time complexity of Func1() is O(N^2)
Some algorithms have the best, worst and average complexity
Worst case: maximum number of runs of any input scale (upper bound)
Best case: minimum number of runs of any input scale (lower bound)
Average situation: expected number of runs of any input scale
For example, search for a data x in an array of length N
Best case: find it at once
Worst case: found N times
Average: N/2 times
In practice, we usually focus on the worst-case operation of the algorithm, so the time complexity of searching data in the array is O(N)
Time complexity calculation case
Case 1
The time to calculate Func(2) is calculated by complexity
void Func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
The first loop is executed 2 * N times, and the second loop is executed 10 times, with a time complexity of O(N)
Case 2
void Func4(int N) {
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}
The cycle runs 100 times in total, which is constant times, and the time complexity is O(1)
Case 3
void Func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}
The two cycles Run M+N times, so the time complexity is O(M+N)
If M > > N, the time complexity is O(M)
If M < < n, the time complexity is O(N)
If M and N are almost large, the time complexity is O(M+N)
Case 4
// The time complexity of calculating strchr? const char * strchr ( const char * str, int character );
strchr is an algorithm to find a character in a string. To find a character in a string, you must traverse the whole string. Then the upper bound is N, the lower bound is 1, and the average is N/2, so the time complexity is O(N)
Case 5
Calculating the time complexity of BubbleSort
void BubbleSort(int* a, int n) {
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
This is a bubble sorting algorithm. The worst case is to run (n-1) + (n-2) +... + 2 + 1 times
Sum n * (n - 1) / 2 times
Then the time complexity is O (N ^2)
Case 6
Calculating the time complexity of BinarySearch
int BinarySearch(int* a, int n, int x) {
assert(a);
int begin = 0;
int end = n-1;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1; }
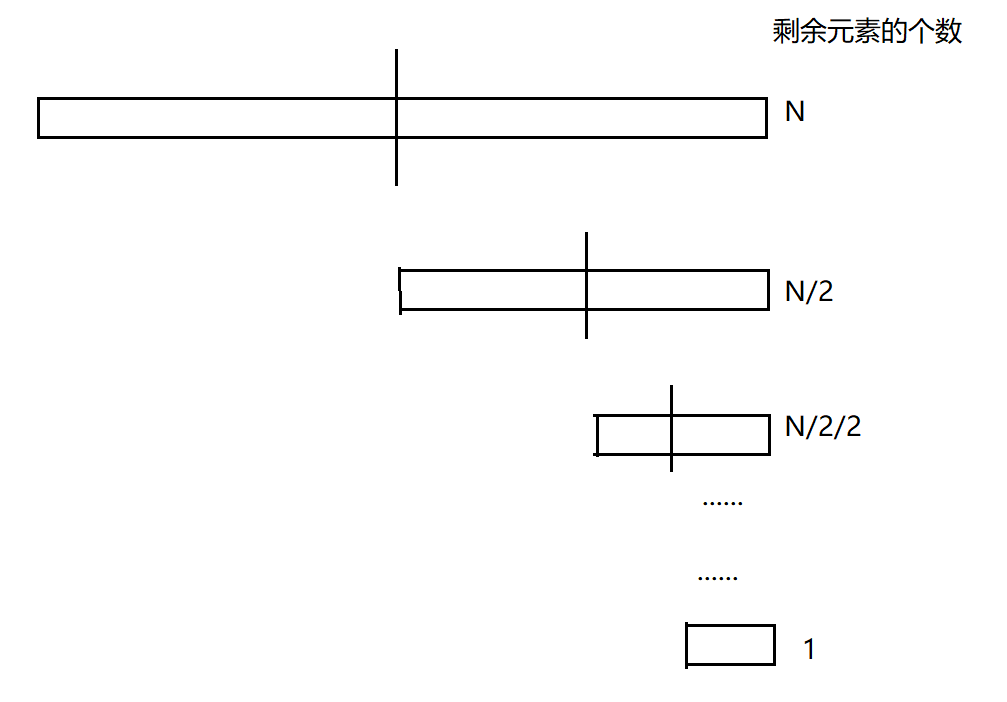
This is a binary search algorithm. The worst case is to keep looking and scoring until there is one number left. Therefore, there is n / 2 / 2 / 2 / 2 /... / 2 = 1. Assuming a total of N times except 2, then N/2n = 1,n = log2N, so the time complexity is O (log2N)
Case 7
Time complexity of computing factorial recursive Fac
long long Fac(size_t N) {
if(0 == N)
return 1;
return Fac(N-1)*N; }
F(N) = N * F(N - 1)
F(N - 1) = (N - 1) * F(N - 2)
F(N - 2) = (N - 2) * F(N - 3)
... ...
...
F(1) = 1
It recurses N times, so the time complexity is O(N)
Case 8
Calculating the time complexity of Fibonacci recursive Fib
Computational Fibonacci recursion Fib Time complexity?
long long Fib(size_t N) {
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
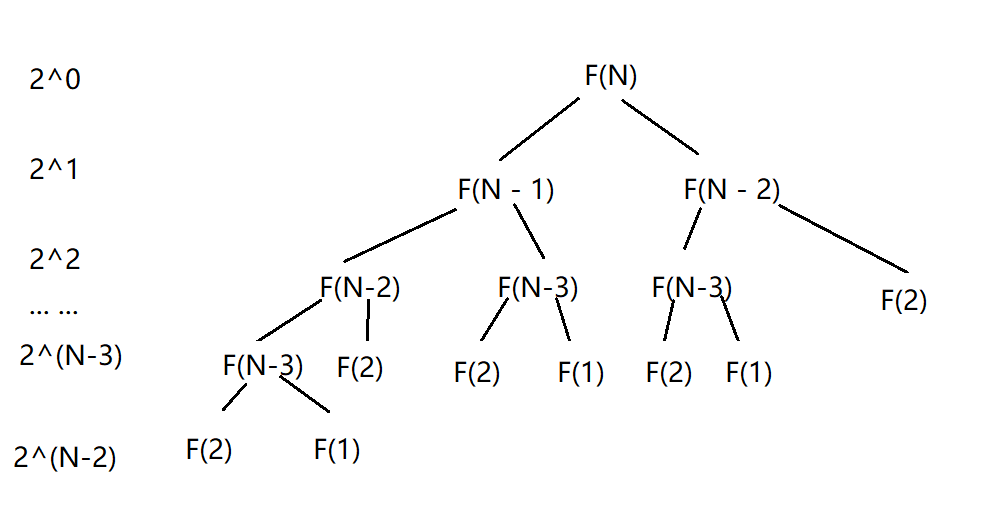
Call 20 + 21 +... + 2(N-2) times in total, and the time complexity is O(2N)
Spatial complexity
Space complexity is also a mathematical expression. It is a measure of the amount of storage space temporarily occupied by an algorithm during operation. It is the number of variables, and the large O asymptotic representation is also used.
example
Example 1:
Calculate the spatial complexity of BubbleSort
void BubbleSort(int* a, int n) {
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
The algorithm creates three variables: exchange, I and end, which are constants and the time complexity is O (1)
Example 2:
long long* Fibonacci(size_t n) {
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray; }
In the heap area, an additional space of (n+1) * 8 bytes is opened up, and the others are constant times, so the space complexity is O(N)
Example 3:
long long Fac(size_t N) {
if(N == 0)
return 1;
return Fac(N-1)*N; }
It recurses N times and opens up a constant space in the stack area each time, so the space complexity is O(N)
Complexity exercise
Disappearing numbers
The array nums contains all integers from 0 to N, but one of them is missing. Please write code to find the missing integer. Do you have a way to finish it in O(n) time?
Method 1: sort all numbers from small to large, and judge whether the previous number + 1 is equal to the next number. If not, find out the number. However, the time complexity of bubble sorting does not meet O(N), so this method does not work
Method 2: sum all numbers from 0 to N, and then subtract the sum of all known numbers to obtain the required number. The time complexity is O(N)
int missingNumber(int* nums, int numsSize){
int sum = 0;
for(int i = 0; i< numsSize+1;i++)
{
sum+=i;
}
for(int i = 0;i <numsSize;i++)
{
sum-=nums[i];
}
return sum;
}
Method 3: use XOR method. First of all, we should know that n ^ 0 = n,n ^ n = 0,a ^ b ^ c = a ^ c ^ b, then use 0 to XOR all the elements in the array, and then XOR the obtained result with the number between 0 and N again. At this time, the number XOR after two times is 0, and the final result is the desired number
int x=0;
for(int i=0;i<numsSize;++i)
{
x^=nums[i];
}
for(int i=0;i<=numsSize;++i)
{
x^=i;
}
return x;
Rotate array
Give you an array, rotate the elements in the array K positions to the right, where k is a non negative number
Method 1: rotate the elements in the array K positions to the right. After the rotation of the ith element, the new position is (i + k)% numsize
nt newnums[numsSize] = 0;
for (int i = 0; i < numsSize; i++)
{
newnums[(i + k) % numsSize] = nums[i];
}
for (int i = 0; i < numsSize; i++)
{
nums[i] = newnums[i];
}
Method 2:
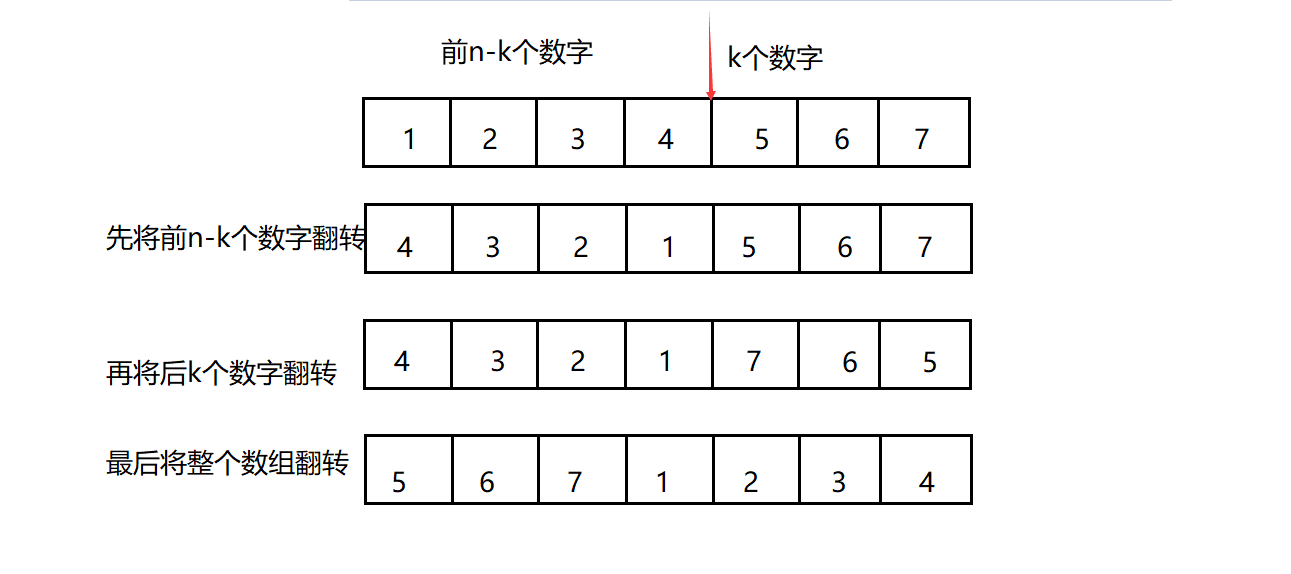
void reverse(int* nums,int begin,int end)
{
while(begin<end)
{
int tmp=0;
tmp=nums[begin];
nums[begin]=nums[end];
nums[end]=tmp;
++begin;
--end;
}
}
void rotate(int* nums, int numsSize, int k)
{
reverse(nums,0,numsSize-k%numsSize-1);
reverse(nums,numsSize-k%numsSize,numsSize-1);
reverse(nums,0,numsSize-1);
}