catalogue
Recursive implementation of factorial
Shortest path problem with multiple sources and targets
Comparison of sorting algorithms
Method of constructing hash function
Object oriented programming
Four characteristics of object-oriented:
-
encapsulation
-
inherit
-
polymorphic
-
Overload (do not overload if three major features are asked)
1. Encapsulation: class encapsulation is to expose the public and connect with other classes to facilitate modification, while hiding the private.
Benefits of encapsulation:
-
Data and member functions are more closely combined
-
Object makes it easier to find errors
-
Object can hide some details from other objects, so that some operations are not affected by other objects.
2. Inheritance:
-
The derived class inherits all members of the base class and does not need to be defined repeatedly
-
Public inheritance means that the properties of the derived class and the base class members are consistent. Protected inheritance means that all members in the derived class are protected. Private inheritance means that all members of the derived class are private.
-
A derived class can override the definition of a member function by introducing its own definition. (override function)
-
A derived class does not necessarily have only one base class. It can be derived from multiple base classes.
3. Polymorphism: polymorphism refers to the ability to obtain multiple forms. In OPP, polymorphism uses the same function name to represent multiple functions, which are members of different objects.
Benefits of polymorphism:
-
Improved code maintainability
-
Increased code extensibility
4. Standard template library (STL):
Containers to know:
Deque (double ended queue), list, stack, queue, vector
The standard template library includes three types of common items: container, iterator and algorithm
-
S tack, queue container does not support generation selector,
-
deque and vector can support almost all iterators.
-
list does not support greater than or less than, addition and subtraction, and + = and - = ".
Complexity analysis
Algorithm complexity can be divided according to time or space complexity. Representative algorithms of each complexity:

Linked list
Unidirectional linked list
Insert & delete
// intSLList.h
class IntSLlNode //A node class includes a stored value and a pointer to the next node
{
public:
IntSLLNode()
{
next=0;
}
IntSLLNode(int el,IntSLLNode *ptr)
{
info=el;
next=ptr;
}
int info;
IntSLLNode *next;
};
class IntSLList //Linked list class
{
public:
IntLList()
{
head=tail=0; //Initialization head and tail equal to 0
}
~IntSLList(); //Destructor
int isEmpty()
{
return head=0;
}
void addToHead(int); //Insert data in front of the linked list
void addToTail(int);//Insert data after linked list
int deleteFromHead();//Delete the first node and return the data of the first node
int deleteFromTail();//Delete the last node and return the data of the node
void deleteNode(int);//Delete nodes with data anywhere
bool isInList(int) const;//Determine whether the data is in this linked list
private:
IntSLLNode *head,*tail;
};
//intSLList.cpp
#include<iostream>
#include"intSLList.h"
using namespace std;
IntSLList::~IntSLList()
{
for(IntSLLNode *p;!isEmpty(); )//Delete each node one by one
{
p=head->next;
delete head;
head=p;
}
}
/*Add node in front of linked list
(1)Create an empty node
(2)Initialize the info member of this node to a specific integer
(3)Add the node to the front of the linked list, and use its next member to point to the pointer of the first node in the linked list, that is, the current value of head
(4)head Pointer to new node*/
void IntSLList::addToHead(int el)
{
head=new IntSLLNode(el,head);//First create a node whose info is el, next points to the head node of the linked list, and then let the head point to el;
if(tail==0) //After adding nodes, judge whether there is only one node in the linked list
tail=head;
}
/*Add a node to the end of the linked list
(1)Create an empty node
(2)Initialize the info member of this node to an integer el
(3)Because the node is to be added to the end of the linked list, set its next member to null
(4)Let the last node of the linked list next point to this node
(5)tail The pointer points to the node*/
void IntSLList::addToTail(int el)
{
if(tail!=0) //If the linked list is not empty
{
tail->next=new IntSLLNode(el);//The next member is empty, so no parameters are passed in
tail=tail->next;
}
else head=tail=new IntSLLNode(el);
}
/*Before deleting a node:
Two special cases are considered
(1)An attempt was made to delete a node from an empty linked list
(2)The linked list of nodes to be deleted has only one node (after deletion, it becomes an empty linked list, and both tail and head are null)
If the deleted node is empty, there are two solutions:
(1)Use assert statement (program termination)
(2)Throw exception
To avoid confusion between a node with a return value of 0 and an empty node, you can let the function return a pointer to an integer instead of an integer.
The deletion operation includes deleting the node at the beginning of the linked list and returning the stored value.*/
int IntSLList::deleteFromHead()
{
int el=head->info;
IntSLLNode *tmp=head; //Create a new node to point to the first node, then move the head back and delete the first node
if(head==tail) //There is only one node in the linked list
head=tail=0;
else head=head->next;
delete tmp;
return el;
}
/*Node after deletion:
(1)Because there is no tail precursor node, we need to traverse the chain until we find the tail precursor node.
(2)Then delete the tail node
(3)Point tail to the new tail node.*/
int IntSLList::deleteFromTail()
{
int el =tail->info;
if(head==tail)
{
delete head;
head=tail=0;
}
else //The number of nodes in the linked list is greater than 1
{
IntSLLNode *tmp;//Find the first node of tail
for(tmp=head;tmp->next!=tail;tmp=tmp->next);
delete tail;
tail=tmp;
tail->next=0;
}
return 0;
}
/*To delete a node with a specific value:
(1)Because you are not sure where the node is, first traverse the linked list to find the location of the node
(2)Traverse the linked list to find the precursor node of the node
(3)Delete operation*/
void IntSLList::deleteNode(int el)
{
if(!head=0) //If the linked list is not empty
if(head==tail&&el==head->info)//If the linked list has only one node and this node is to be deleted
{
delete head;
head=tail=0;
}
else if(el==head->info) //If there is more than one node, the number to be deleted is just the first node
{
IntSLLNode *tmp=head;
head=head->next;
delete tmp;
}
else{
IntSLLNode *pred,*tmp;
for(pred=head,tmp=head->next;tmp!=0&&!(tmp->info==el);pred=pred->next,tmp=tmp->next);
if(tmp!=0)
{
pred->next=tmp->next;
if(tmp==tail) //The last node is to be deleted
tail=pred;
delete tmp;
}
}
}
bool IntSLList::isInList(int el)const
{
IntSLLNode *tmp;
for(tmp=head;tmp!=0&&!(tmp->info=e=l);tmp=tmp->next);
return tmp!=0;
}
lookup
Traverse the linked list, compare the stored value with the stored value of the linked list with the temporary variable, and exit the loop if it is equal
Bidirectional linked list
Each node of the linked list has two pointers, one to the predecessor and one to the successor, which is called a two-way linked list
-
Post insert node
-
Create a new node
-
Assign a new node
-
The next member of the new node is set to null
-
Point the prev (pointer to the predecessor node) of the new node to the tail (pointer to the original last node)
-
Point tail to the new node
-
Point the next of the predecessor node to the new node
-
Circular linked list
Single loop linked list - in a single linked list, change the pointer and null of the terminal node to point to the header node or the start node
Advantages of circular linked list:
-
When traversing, terminate the loop without judging that the pointer is null (the loop linked list is not null)
-
From any point, you can go to any other point in the linked list
Jump linked list
Search of jump linked list
-
Start searching from the pointer at the top level. If you find this element, you can borrow a book to find it
-
If the end of the linked list is reached or a value larger than the element is encountered, the key will be searched from the node in front of the key, starting from the pointer one level lower than the previous node
-
Loop through the above process until the element is found
Sparse table
The best way is to use two one bit linked list arrays
Stack and queue
Stack: (last in, first out)
Basic operation of stack:
-
clear() -- clear stack
-
isEmpty() -- judge whether the stack is empty
-
push(e1) - put element e1 at the top of the stack
-
pop() -- pop up the element at the top of the stack (with deletion and without getting the value of the element)
-
topEl() -- get the element at the top of the stack, but do not delete it.
//Vector implementation of stack
#include<vector>
template<class T,int capacity=30>
class Stack
{
public:
Stack()
{
pool.reserve(capacity);
}
void clear()
{
pool.clear();
}
bool isEmpty()const
{
return pool.empty();
}
T& topEl()
{
return pool.back();
}
T pop()
{
T el=pool.back();
pool.pop_back();
return el;
}
void push(const T&el)
{
pool.push_back(el);
}
private:
vector<T>pool;
};
//Linked list implementation of stack
#include<list>
template<class T>
class LLStack
{
public:
LLStack()
{
}
void clear()
{
lst.clear();
}
bool isEmpty()const
{
retuen lst.empty();
}
T& topEL()
{
return lst.back();
}
T pop()
{
T el=lst.back();
lst.pop_back();
return el;
}
void push(const T& el)
{
lst.push_back(el);
}
private:
list<T>lst;
};
The implementation form of linked list is more matched with the abstract stack.
In the implementation form of vector and linked list, the running time of out of stack and in stack operation is O(1), but in the implementation form of vector, pressing an element into a full stack needs to allocate more storage space, and all elements in the existing vector need to be copied to a new vector. Therefore, in the worst case, it takes O(n) time to complete the stack operation
Queue: (first in, first out)
Basic operations of queue:
-
clear() -- clear the queue
-
isEmpty() -- judge whether the queue is empty
-
enqueue(e1) -- add element e1 at the end of the queue
-
dequeue() -- get the first element of the queue
-
firstEI() -- get the first element of the queue, but do not delete it
//Array implementation of queue
template<class T,int size=100>
class ArrayQueue
{
public:
ArrayQueue()
{
first=last=-1;
}
void enqueue(T);
T dequeue();
bool isFull()
{
return first==0&&last==size-1||first==last+1; //There are two cases when the array is full
}
bool isEmpty()
{
return first==-1;
}
private:
int first,last;
T storage[size]; //An array that implements a queue
};
template<class T,int size>
void ArrayQueue<T,size>::enqueue(T el)
{
if(!isFull)
{
if(last==-1||last==size-1) //If the linked list is empty or the last element of the queue is at the last position of the array
{
storage[0]=el;
last=0;
if(first==-1)
first=0;
}
else storage[++last]=el;
}
else cout<<"Full queue\n";
}
template<Class T,int size>
T ArrayQUeue<T,size>::dequeue()
{
T tmp;
tmp=storage[first];
if(first==last) //The queue has only one element
last=first=-1;
else if(first==size-1)
first=0;
else first++;
return tmp;
}
//Linked list implementation of queue
#include<list>
template<class T>
class Queue
{
public:
Queue()
{
}
void clear()
{
lst.clear();
}
bool isEmpty()const
{
return lst.empty();
}
T& front()
{
return lst.front();
}
T dequeue()
{
T el=lst.front();
lst.pop_front();
return el;
}
void enqueue(const T& el)
{
lst.push_back(el);
}
private:
list<T>lst;
};
Queue with two stacks
Stack 1 is used to insert data
Stack 2 is used to delete the data inserted by stack 1
Stack with two queues
Use a queue to put the data stored in the stack, then delete all the numbers in front of the last number, insert the end of the deleted number into queue 2, and then the elements in queue 1 are out of the queue, so as to realize LIFO.
recursion
Function calls and recursive implementations:
The state of each function (including the main function) is determined by the following factors:
-
The contents of all local variables in the function
-
Parameter value of function
-
The return address indicating where the function was restarted
The data area that contains all this information is called the active record or stack framework.
The life of activity records is generally short. Get the dynamically allocated space when the function starts to execute, and release its space when the function exits.
No matter what function is called by, an activity record is established in the runtime stack. The runtime stack always reflects the current state of the function.
Recursive call is not the function call itself on the surface, but an instance of a function calls another instance of the same function. These calls are internally represented as different activity records and are distinguished by the system.
Recursive implementation of factorial
double power(double x,unsigned int n)
{
if(n==0)
return 1.0;
else
return x*power(x,n-1);
}Iterative factorization of n
//In fact, iteration is to find factorial by cyclic method
int main()
{
int val,i,mult=1;
cout<<"val="<<val<<endl;
for(i=0;i<=val;i++)
mult=mult*i;
cout<<mutl<<endl;
return 0;
}to flash back
//Pseudo code of eight queens
putQueen(row)
for Same line row Each location on the col
if position col You can put the queen
Put the next queen in position col Division;
if(row<8)
putQueen(row+1);
else success;
Removal position col Queen ofIdea:
-
Set an 8 * 8 array to represent the chessboard, and initialize all values to 1
-
Whenever a queen is placed, set the position where the queen cannot be placed to 0
-
During backtracking, reset these positions set to 0 to 1 (that is, the queen can be placed)
Binary tree
Basic concepts:
-
The root node of the tree is at the top and the leaf node is at the bottom
-
The empty result is an empty tree
-
The height of the empty tree is 0
-
A tree with a height of 1 for a single node (the node is both root and leaf)
The height of a non empty tree is the maximum level of nodes in the tree
The hierarchy of nodes is the length of the path from the root node to the node plus 1
There is one node in the first layer, two nodes in the second layer, and four nodes in the third layer until layer i
A tree with 2^i nodes is called a complete binary tree
Characteristics of binary lookup tree (ordered binary tree):
For each node n in the tree, the value in its left subtree (the tree whose root node is the left child node) is less than the value v in node n, and the value in its right subtree is greater than the value v in node n.
Implementation of binary tree:
Binary tree can be realized in two ways:
-
Array (vector)
-
Link structure
A new implementation is to use classes to implement trees
A node is an instance of a class that consists of an information member and two pointer members. This node is used and manipulated by member functions of another class that treats the tree as a whole.
//genBST.h
#include<queue>
#include<stack>
using namespace std;
template<class T>
class Stack:public stack<T>
{
}
template <class T>
class Queue:public queue<T>
{
T dequeue()
{
T tmp=front();
queue<T>::pop();
return tmp;
}
void enqueue(const T& el)
{
push(el);
}
};
template<class T>
class BSTNode
{
public:
BSTNode()
{
left=right=0;
}
BSTNode(const T&e,BSTNode<T>*l=0,BSTNode<T>*r=0)
{
el=e;
left=l;
right=r;
}
T el;
BSTNode<T> *left,*Right;
};
template<class T>
class BST
{
public:
BST()
{
root=0;
}
~BST()
{
clear();
}
void clear()
{
clear(root);
root=0;
}
bool isEmpty()const
{
return root==0;
}
void preorder()
{
preorder(root);
}
void inorder()
{
inorder(root);
}
void postorder()
{
postorder(root);
}
T* search(const T&el)const
{
return search(root,el);
}
void breadthFirst(); //Breadth first traversal from top to bottom and from left to right
void iterativePreorder(); //Non recursive implementation of preorder traversal
void iterativeInorder(); //Non recursive implementation of middle order traversal
void iterativepostorder(); //Non recursive implementation of postorder traversal
void insert(const T&); //insert
protected:
BSTNode<T>* root;
void clear(BSTNode<T>*);
T* search(BSTNode<T>*,const T&)const;
void preorder(BSTNode<T>*);
void inorder(BSTNode<T>*);
void postorder(BSTNode<T>*);
virtual void visit(BSTNode<T>*p)
{
cout<<p->el<<' ';
}
};Search of binary search tree
Worst case O(n)
template<class T>
T* BST<T>::search(BSTNode<T>*p,const T& el)const
{
while(p!=0)
if(el==p->el)
return &p->el;
else if(el<p->el)
p=p->left;
else p=p->right;
return 0;
}breadth-first search
//Breadth first traversal from top to bottom and from left to right
template <class T>
void BST<T>::breadthFirst()
{
Queue<BSTNode<T>*>queue; //Define a queue of type node pointer
BSTNode<T>* p=root;
if(p!=0)
{
queue.enqueue(p);
while(!queue.empty())
{
p=queue.dequeue();
visit(p);
if(p->left!=0)
queue.enqueue(p->left);
if(p->right!=0)
queue.enqueue(p->right);
}
}
}Depth first traversal
//Medium order traversal
template<class T>
void BST<T>::inorder(BSTNode<T>*p)
{
if(p!=0)
{
inorder(p->left);
visit(p);
inorder(p->right);
}
}
//Preorder traversal
template<class T>
void BST<T>::preorder(<BSTNode<T>*p)
{
if(p!=0)
{
visit(p);
preorder(p->left);
preorder(p->right);
}
}
//Postorder traversal
template<class T>
void BST<T>::postorder(BSTNode<T>*)
{
if(p!=0)
{
postprder(p->left);
postorder(p->right);
visit(p);
}
}
//Non recursive implementation of preorder traversal
template<class T>
void BST<T>::iterativePreorder()
{
Stack<BSTNode<T>*>travStack;
BSTNode<T>* p=root;
if(p!=0)
{
travStack.push(p);
while(!travStack.empty())
{
p=travStack.pop();
visit(p);
if(p->right!=0) //The stack is first in first out, so put it on the right and then on the left
travStack.push(p->right);
if(p->left!=0)
travStack.push(p->left);
}
}
}
//Non recursive implementation of post order traversal
template<class T>
void BST<T>::iterativeinorder()
{
Stack<BSTNode<T>*>travStack;
BSTNode<T>* p=root,*q=root;
while(p!=0)
{
for(;p->left!=0;p=p->left)
travStack.push(P);
while(p->right==0||p->right==q)
{
visit(p);
q=p;
if(travStack.empty())
return;
p=travStack.pop();
}
travStack.push(p);
p=p->right;
}
}
//Non recursive implementation of middle order traversal
template<class T>
void BST<T>::iterativeinorder()
{
Stack<BSTNode<T>*>travStack;
BSTNode<T>*p=root;
while(p!=0)
{
while(p!=0)
{
if(p->right)
travStack.push(p->right);
travStack.push(p);
p=p->left;
}
p=travStack.pop();
while(!travStack.empty()&&p->right==0)
{
visit(p);
p=travStack.pop();
}
visit(p);
if(!travStack.empty())
p=travStack.pop();
else p=0;
}
}Tree balance:
If the height difference between two subtrees of any node in the tree is 0 or 1, the binary tree is highly balanced, or called balanced
Recursive algorithm of balanced tree
template<class T>
void BST<T>::balance(T data[],int first,int last)
{
if(first<=last)
{
int middle=(first+last)/2;
insert(data[middle]);
balance(data,first,middle-1);
balance(data,middle+1,last);
}
}Idea:
-
Find the intermediate node ((first+last)/2) as the root node
-
Find the middle node between the front point and the middle point as the left child node
-
Then find the middle point to become the left child node of the left child node
-
After the loop knows to get to the front point, the remaining points in front of the root node are inserted into the remaining nodes of each layer in order
AVL tree
heap
Heap is a special type of binary tree, which has the following two properties:
-
The value of each node is greater than or equal to the value of each child node
-
The tree is completely balanced, and the leaves of the last layer are in the leftmost position
Make heap a priority queue
Complexity O(lgn)
-
Add element to priority queue
To queue an element, you can add it to the end of the heap as the last leaf node. In order to maintain the nature of the heap, the last leaf node can be moved to the root when adding elements
//Pseudo code
heapEnqueue(el)
take el At the end of the heap;
while el Not at the root and el>parent(el)
el Exchange with its parent node;-
Delete the element from the priority queue p to delete the element from the heap, you need to delete the root element from the heap, because the root element has the highest priority according to the nature of the heap. Then put the last leaf node on the root node, almost certainly to restore the nature of the heap. At this time, you can move the root node down the tree
//Pseudo code
heapDequeue()
Extract elements from root node;
Place the element in the last leaf node where you want to delete the element;
Delete the last leaf node;
//Both subtrees of the root are heaps
p=Root node;
while p Is not a leaf node, and p Any child node smaller than it
exchange p Its larger child nodes;
//Algorithm implementation of moving the root element down the tree
template<class T>
void moveDown(T data[], int first, int last)
{
int largest = 2 * first + 1;
while (largest <= last)
{
if (largest < last && data[largest] < data[largest + 1])
largest++;
if (data[first] < data[largest])
{
swap(data[first], data[largest]);
first = largest;
largest = 2first + 1;
}
else largest = last + 1;
}
}chart
Concept of diagram:
The figure is divided into:
-
Directed graph
-
Undirected graph
Edge set:
-
Digraph: (v1, v2)
-
Simple graph (undirected graph): {v1, v2}
Difference between loop and loop:
-
Ring: all vertices in the circuit are different, which is called a ring
-
Loop: in a directed graph, starting from a certain point without passing through the repeated edge, and finally returning to the point through the edge. Example: a - > b - > C, a - > C is a ring, but not a loop a - > b, B - > C, C - > A is a loop and a loop
Representation of Graphs
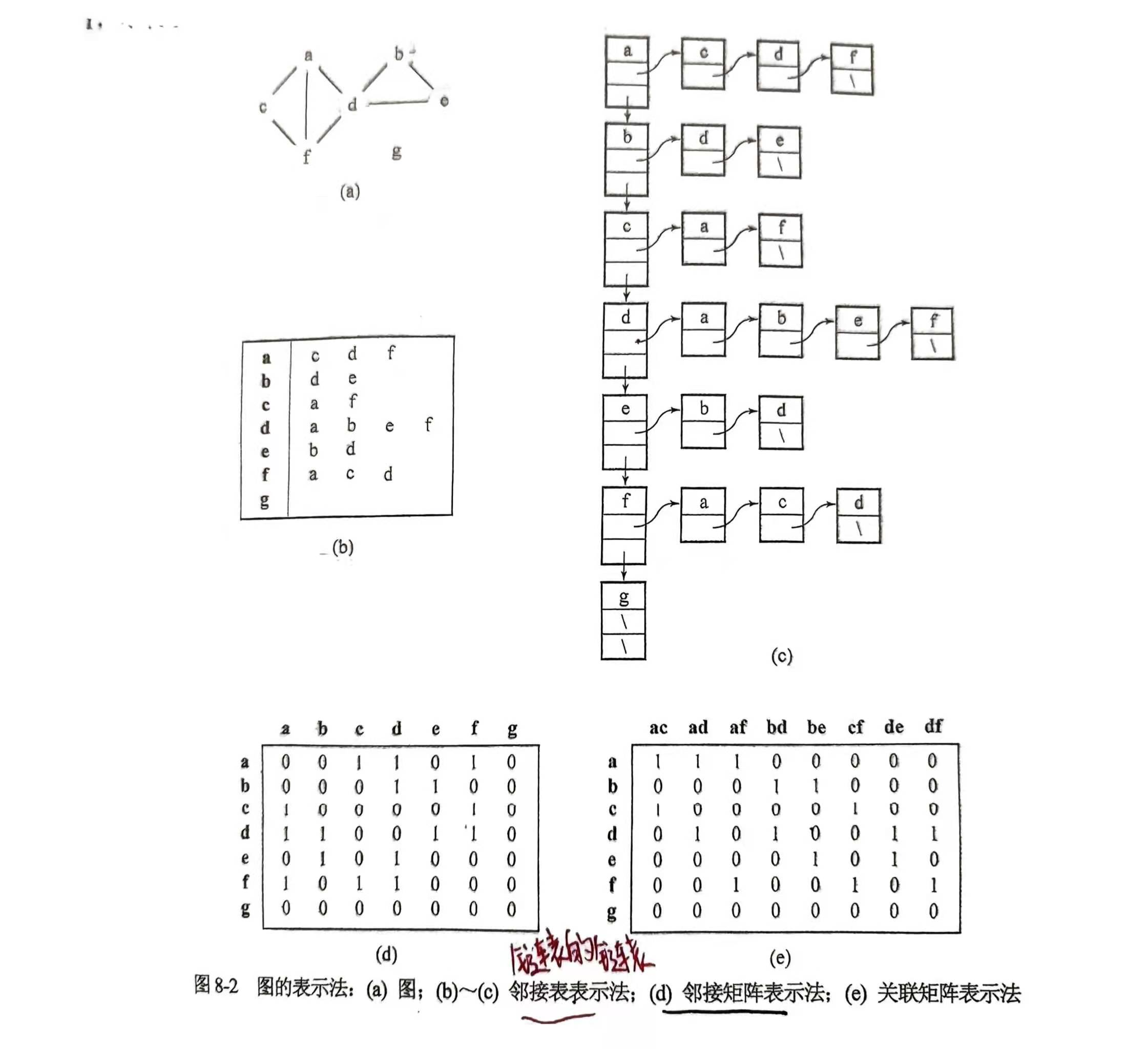
Traversal of Graphs
Depth first traversal
DFS(V)
num(V)=i++; //First num(V)=1, then i++
for vertex v All adjacency points of u //Loop through all vertices of v
if num(u)=0
Edge edge(uv)Add edge set edges;
DFS(u);
depthFirstSearch()
for All Vertices v
num(v)=0; //Number all vertices to 0
edges=null; //Set of edges
i=1;
while There is a vertex v send num(v)=0 //The loop condition is whether the vertex has not been accessed, number or 0
DFS(v);
Output edge set edges;
Breadth traversal
breadFirstSearch()
for All Vertices u
num(u)=0; //Number all vertices to 0
edges=null; //Set of edges
i=1;
while There is a vertex v send num(v)Is 0 //There are vertices that have not been traversed
num(v)=i++;
enqueue(v);
while Queue is not empty
v=dequeue();
for vertex v All adjacency points of u //Number and queue all adjacent contacts of vertex v first
if num(u)Is 0
num(u)=i++;
enqueue(u);
Edge edge(vu)Add to edges Medium;
output edges;
Dijkstra algorithm:
Operation steps:
-
First, define an array D, where D[v] represents the weight of the edge from the source point s to the vertex v. if there is no edge, set D[v] to infinity
-
The vertex set of a graph is divided into two sets s and V-S. The first set s represents the set of vertices whose shortest path from the source point has been determined, that is, if a vertex belongs to the set s, it means that the shortest path from the source point s to the point is known. The remaining vertices are placed in another set V-S
-
Each time, take out a vertex u with the smallest length of the shortest special path from the set V-S whose shortest path length has not been determined, add u to the set S, and modify the shortest path length reachable by S in array D. If the shortest special path length of VI becomes shorter when u of set S is added as the middle vertex, modify the distance value of VI (that is, when d [u] + w [u, vi] < d [vi], make D[vi] = D[u] + W[u, vi])
-
Repeat the operation in step 3. Once s contains all the vertices in V, the distance value of each vertex in D records the shortest path length from the source point s to the vertex.
DijkstraAlgorithm(Weighted simple directed graph digraph,vertex first)
for All Vertices v
currDist(v)=∞;
currDist(first)=0;
toBeChecked=All Vertices ; //V-S set
while toBeChecked Non empty
v=toBeChecked in currDist(v)Smallest vertex;
from toBeChecked Delete in v;
for toBeChecked in v All adjacent vertices of u
if currDist(u)>currDist(v)+weight(edge(vu))
currDist(u)=currDist(v)+weight(edge(vu));
predecessor(u)=v;Shortest path problem with multiple sources and targets
Find the shortest path from any vertex to any other vertex
WFIalgorithm(matrix weight)
for i=1 to |V| //i is the middle point
for j=1 to |V| //j is the starting point
for k=1 to |V| //k is the end point
if weight[j][k]>weight[j][i]+weight[i][k]
weight[j][k]=weight[j][i]+weight[i][k]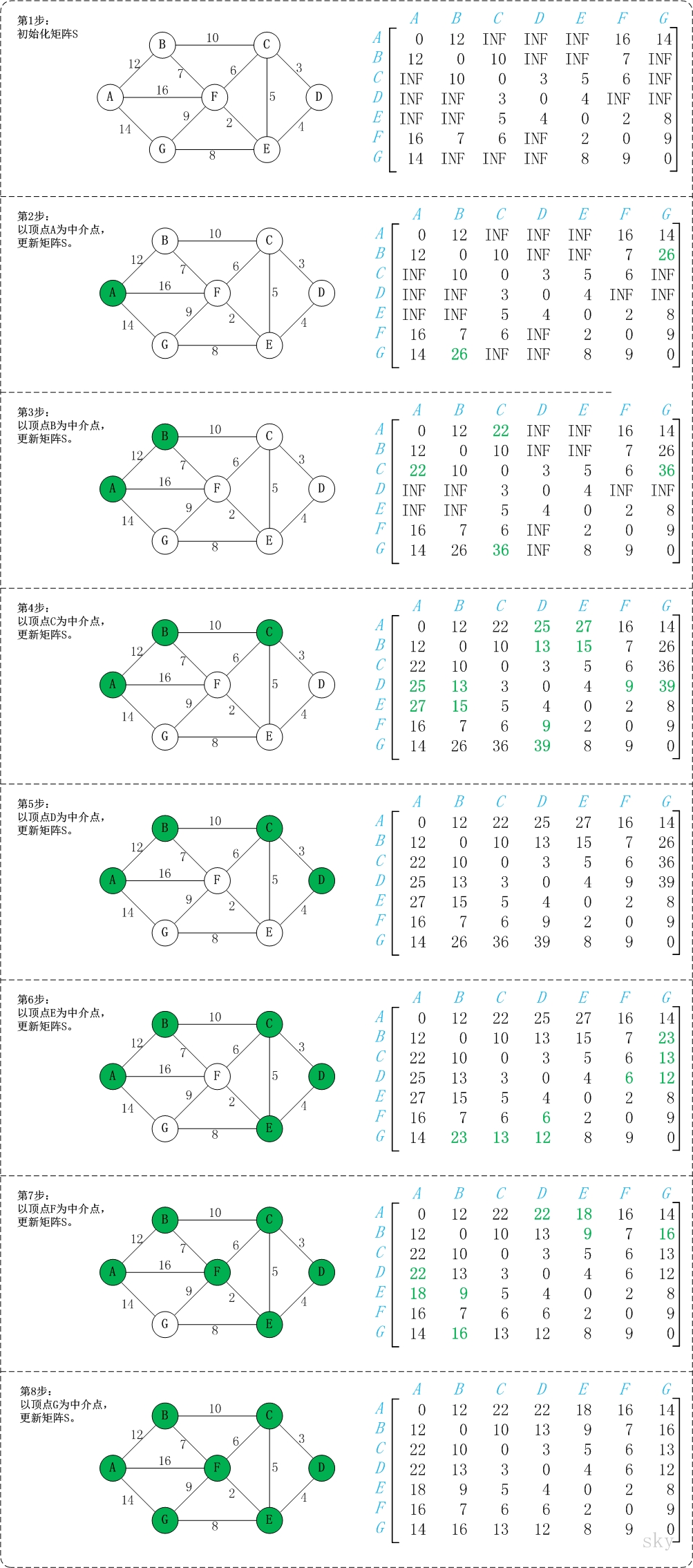
Spanning tree
Steps for Kruskal to realize spanning tree: (merge edges, start from the smallest edge, and add the edges that do not form a ring to the tree)
-
Arrange column edges from large to small by weight
-
Start the tree from the two vertices of the least weighted edge
-
If the added edges are not connected, merge the two subtrees (Note: the essence of connection is to find out whether the two subtrees have the same parent node. In the figure, it refers to whether there is a common maximum connection point, such as v4 - > V7 and v6 - > v7. When v4 and v6 are connected, they are connected because they have a common parent node)
-
Merge subtrees from remaining minimum edges
KruskalAlgorithm(Weighted connected undirected graph graph)
tree=null;
edges=graph All sequences sorted by edge weights in;
for(i=1;i<|E|And|tree|<|V|-1;i++)
if edges Medium ei Not with tree Edges in form a ring
take ei join tree;Dijestra implementation spanning tree
-
The edges are added to the tree one by one. If a ring is detected, the edge with the largest weight in the ring is deleted
DijkstraMethod(Weighted connected undirected graph graph)
tree=null;
edges=graph An unordered sequence of all edges in;
for j=1 to |E|
take ei Add to tree in;
if tree Middle ring
Removes the edge with the largest weight from the ring;sort
Insert sort
1. Compare the first two numbers first
2. Then consider the third number, four, five
//First, use the outer loop to obtain the number data[i] (tmp=data[i]) to be compared, and then use the inner loop to make j and other I the current position, and compare the number (tmp) with the previous number (data[j-1]) one by one. If tmp is less than the previous number, copy the number to the next position, and then put tmp to the appropriate position data[j]
//Pseudo code
insertionsort(data[],n)
for i=1 reach n-1
Will be greater than data[i]All elements of are moved to one position, and data[i]Put it in the right place
//code
template<class T>
void insertionsort (T data[],int n)
{
for(int i=1;i<n;i++)
{
T tmp=data[i];
for(int j=i;j>0&&tmp<data[j-1];j--)
data[j]=data[j-1];
data[j]=tmp;
}
}Select sort
First find the smallest element in the array, exchange it with the element in the first position, and then add data [1] Find the smallest element in data [n-1] and put it in the second position
//Pseudo code
selectionsort(data[],n)
for i=0 reach n-2
Find elements data[i],...,data[n-1]The smallest element in the;
Compare it with data[i]exchange
//code
template<class T>
void selectionsort(T data[],int n)
{
int min;
for(int i=0;i<n-1;i++)
{
for(int j=i+1,min=i;j<n;j++) //Find the subscript of the minimum value
if(data[j]<data[min])
min=j;
swap(data[min],data[i]);
}
}Bubble sorting
The array is compared from the last two numbers (data[n-1] and data[n-2]). If the order is reversed, the two numbers are exchanged, and then data[n-2] and data[n-3], similarly, until data[1] and data[0], so that the smallest number reaches the top of the array
//Pseudo code
bubblesort(data[],n)
for int i=0 reach n-2
for int j=n-1 Down to i+1
If the two are in reverse order, the positions are exchanged j And location j-1 Element of
//code
template<class T>
void bubblesort(T data[],int n)
{
for(int i=0;i<n-1;i++)
{
for(int j=n-1;j>i;j--)
if(data[j]<data[j-1])
swap(dara[j],data[j-1]);
}
}//Bubble sort} if there is no exchange at one time, the sorting process will stop
template<class T>
void bubblesort(T data[],const int n)
{
bool again=true;
for(int i=0;i<n-1&&again;i++)
{
for(int j=n-1,again=false;j>i;j--)
if(data[j]<data[j-1])
{
swap(dara[j],data[j-1]);
again=true;
}
}
}Heap sort
A binary tree with the following two properties when heap
1. The value of each node will not be less than the value of its child nodes
2. The tree is completely balanced, and the bottom leaf nodes are located on the leftmost position
The elements in the heap will not be arranged completely in order. The only certainty is that the largest element is located at the root node. Heap sorting starts from the heap, puts the largest element at the end of the array, and then rebuilds the heap with one element missing
//Heap sort pseudo code
heapsort(data[],n)
Array data Convert to heap
for i=down to 2
Connect the root node to the location i Element exchange location for
Recovery tree data[0],...data[i-1]Heap properties for
//code
//
template<class T>
void moveDown(T data[],int first,int last)
{
int c1=2*first+1;
while(c1<=last)
{
if(c1<last&&data[c1]<data[c1+1])
c1++;
if(data[first]<data[c1])
{
swap(data[first],data[c1])
first=c1;
c1=2*first+1;
}
else c1=last+1;
}
}
template<class T>
void heapsort(T data[],int size)
{
for(int i=size/2-1;i>=0;--i)
moveDown(data[],i,size-1);
for(int i=size-1;i>=1;--i)
{
swap(data[0],data[i])
moveDown(data,0,i-1);
}
}Quick sort
The original array is divided into two subarrays. The elements in the first subarray are less than or equal to a selected keyword, which is called boundary or benchmark, and the second subarray is greater than or equal to the boundary value. recursion
quicksort(array[])
if length(array)>1
choice bound; //Divide the array into subarrays subarray1 and subarray2
while array There are elements in it
stay subarray1={el:el<=bound}Contains element;
Or in sybarray2={el:el>=bound}Contains elemen;
quicksort(subarray1);
quicksort(subarray2);
//Select the element in the middle of the array as the boundary value
template<class T>
void quicksort(T data[],int first,int last)
{
int lower=first+1,upper=last;
swap(data[first],data[(first+last)/2]);
T bound=data[first];
while(lower<=upper)
{
while(data[lower]<bound)
lower++;
while(bound<data[upper])
upper--;
if(lower<upper)
swap(data[lower++],data[upper--]);
else lower++;
}
swap(data[first],data[upper]);
if(first<upper-1)
quicksort(data,first,upper-1);
if(upper+1<last)
quicksort(data,upper+1,last);
}
//To realize quick sorting, we need to preprocess the array: find the largest element in the array, exchange it with the last element in the array, and put the largest element at the end of the array to prevent the value of index lower from exceeding the end of the array
template<class T>
void quicksort(T data[],int n)
{
int i=max;
if(n<2)
return;
for(i=1,max=0;i<n;i++)
if(data[max]<data[i])
max=i;
swap(data[n-1],data[max]);
quicksort(data,0,n-2);
}Merge sort
Pseudo code
mergesort(data[],first,last)
if first<last
mid=(first+last)/2;
mergesort(data,first,mid); //Left half of data
mergesort(data,mid+1,last); //Right half of data
merge(data,first,last); ///All the parts are combined into a arranged array
merge(array1[],first,last) //merge
mid=(first+last)/2;
i1=0;
i2=first;
i3=mid+1;
while array1 Both the left subtree group and the right sub array of contain elements
if array1[i2]<array1[i3]
temp[i1++]=array1[i2++];
else temp[i1++]=array1[i3++];
take array1 Import the remaining elements in temp;
take temp Content import in array1;
Comparison of sorting algorithms
| Sorting algorithm | Worst case scenario | Average situation | Best case | Spatial complexity | Is it stable |
|---|---|---|---|---|---|
| Insert sort | O(n²) | O(n²) | O(n) | O(1) | yes |
| Select sort | O(n²) | O(n²) | O(²) | O(1) | no |
| Bubble sorting | O(n²) | O(n²) | O(n) | O(1) | yes |
| Heap sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | no |
| Quick sort | O(n²) | O(nlog2n) | O(nlog2n) | O(log2n) | no |
| Merge sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | yes |
hash
You need to find a function h that can convert a specific keyword K (possibly a string, number or record) into an index of the table, which is used to store items of the same type as K. This function H is called a hash function. (after calculating the keyword with hash function, get a subscript (array), and put the relevant information into the corresponding position of the array)
Hash functions may map two or more different keywords to the same address, which is called "conflict", and these different keywords that collide are called synonyms
The quality of hash function depends on its ability to avoid conflict
Method of constructing hash function
-
Residual method
The simplest method is the remainder method (using modular operation): TSize=sizeof(table), and h(K)=K mod TSize. TSize is preferably prime
-
Folding method
-
Shift folding
For example, the social security number 123-45-6789 is divided into three parts - 123, 456 and 789, and then these three parts are added to obtain the result 1368, and then the modular operation is performed on TSize
-
Boundary folding
For example, the social security number 123-45-6789 is divided into three parts - 123, 654 and 789. Add these three parts to get the result 1566, and then take the modulus operation.
-
-
Square middle method
After the keyword is squared, the middle part of the squared result is used as the address. If the keyword is a string, it must first be processed to produce a number
-
Extraction method
Only part of the keywords are used to calculate the address. For social security number 123-5-6789, use only the first four digits 1234, or only the last four digits 6789
-
Radix conversion method
The radix conversion method converts the keyword K into another digital radix, and then performs modular operation
-
Universal hashing
Conflict resolution
-
open addressing
-
Linear detection
-
Secondary detection method
-
Double hash
-
-
The} keyword of the link method does not need to be placed in the table. In the link method, each address in the table is associated with a linked list or chain structure, The info field is used to save keywords or references to this keyword. The records with all keywords as synonyms are stored in a single linked table. We call this table synonym sub table. Instead of putting synonyms in multiple locations, they are gathered together, and then only the header pointers of all synonym sub tables are stored in the hash table
For hash functions that may cause many conflicts, the link method provides a guarantee that the connection will not fail to find the address. Of course, this will also increase the performance loss of traversing the single linked list when searching
-
Bucket addressing
Put the conflicting elements in the same position in the table, so you can associate a bucket (large enough storage space) for each address in the table. This method can not completely avoid the conflict.
data compression
Huffman coding
definition:
Given a leaf node, construct a binary tree. If the weighted path length of the binary tree reaches the minimum, such a binary tree is called the optimal binary tree, also known as Huffman tree